Dijkstra算法——《算法导论》学习心得(十三)
个人blog迁移到 www.forwell.me
这两天在做一个项目,关于北京市出租车的,然后用到了Dijkstra算法,所以这篇文章就先写Dijkstra算法了。在大二下的时候学了数据结构,书里面也讲了Dijkstra算法,但是当时怎么也没理解,结果考试的时候就考了,哎蛋疼!现在用到了,又得硬着头皮去学,结果很快弄明白了,只是在写代码时出了一些很低级的错误,调Bug用了不少时间。最后总结只能说:不是你不会,而是没到你非会不可的地步!在这篇文章里我就用实际的项目给大家讲Dijkstra算法。
背景:
迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。(我觉得这个算法实质就是每一次你就在所有的路里面找一条最短的路走,这条路走完就不要再走了,在找一条,最后走到你要到的终点就行了,这个过程中没有任何的启发性,所以算法计算量就会很大,对于大型地图是不实际的,都得需要优化。)
算法描述
算法思想:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
算法步骤:
a.初始时,S只包含源点,即S={v},v的距离为0。U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则
b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。
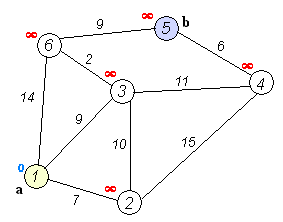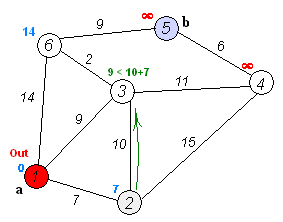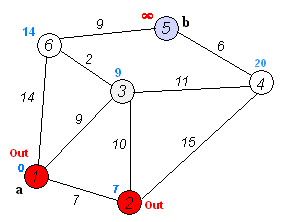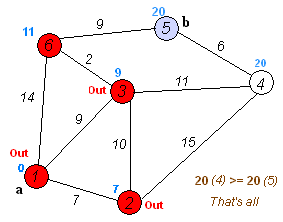
执行动画过程如下图:
我的运用:
在这个项目中我就是需要找到两个点之间的最短路径,然后在图我是用一个ArrayList来存的,没有用连接表或者是矩阵,因为我觉得图就是边的集合,然后再用一个ArrayList来存图的点集,毕竟在算法中我们需要用点,我不能去图里面遍历所有的边,然后在通过边来拿点,应为这样太慢了,整个北京市有218965条路,每一条路还有几百上千的点组成,这个数据就有点大了,尤其对于Dijkstra算法,顶点多了,算法绝对慢。未来解决这些问题,我还建立了两个索引,用map来做的,一个是用来判断一个新的点是否已经加入到顶点集,另一个使用来判断两个点是否直接连接!
先看一些实体类吧:
Point类:
package com.tangbo;
public class Point {
private String pointId;//longitude+latitude构建出来的
private String date;//这个点创造的实际日期,项目需要的属性,大家可以不用管
private double longitude;//经度
private double latitude;//纬度
private String isHavePeople;//项目需要的属性,大家可以不用管
private String roadNum;//项目需要的属性,大家可以不用管
private double ObservProbability;//项目需要的属性,大家可以不用管
private int position;//记录这个点在该路里面是第几个点,因为一条路是由点集构成的,我需要知道这个点在这条路的那个位置
public Point() {
super();
}
public Point(String pointId)
{
this.pointId = pointId;
}
public double getLongitude() {
return longitude;
}
public void setLongitude(double longitude) {
this.longitude = longitude;
}
public double getLatitude() {
return latitude;
}
public void setLatitude(double latitude) {
this.latitude = latitude;
}
public String getDate() {
return date;
}
public void setDate(String date) {
this.date = date;
}
public String getIsHavePeople() {
return isHavePeople;
}
public void setIsHavePeople(String isHavePeople) {
this.isHavePeople = isHavePeople;
}
public String getRoadNum() {
return roadNum;
}
public void setRoadNum(String roadNum) {
this.roadNum = roadNum;
}
public double getObservProbability() {
return ObservProbability;
}
public void setObservProbability(double observProbability) {
ObservProbability = observProbability;
}
public int getPosition() {
return position;
}
public void setPosition(int position) {
this.position = position;
}
public String getPointId() {
return pointId;
}
public void setPointId(String pointId) {
this.pointId = pointId;
}
@Override
public String toString() {
return longitude + "," + latitude;
}
}
LineSegment(路段)类:
package com.tangbo;
public class LineSegment {
private String roadNum;//路段的编号
private Point starPoint;//起点
private Point endPoint;//终点
private double disc;//这段路有多长
public LineSegment() {
super();
}
public LineSegment(Point starPoint, Point endPoint,double disc) {
super();
this.starPoint = starPoint;
this.endPoint = endPoint;
this.disc = disc;
}
public LineSegment(Point starPoint, Point endPoint) {
super();
this.starPoint = starPoint;
this.endPoint = endPoint;
this.disc = Util.calcuDistByCoordinate(starPoint, endPoint);
}
public Point getStarPoint() {
return starPoint;
}
public void setStarPoint(Point starPoint) {
this.starPoint = starPoint;
}
public Point getEndPoint() {
return endPoint;
}
public void setEndPoint(Point endPoint) {
this.endPoint = endPoint;
}
public String getRoadNum() {
return roadNum;
}
public void setRoadNum(String roadNum) {
this.roadNum = roadNum;
}
public double getDisc() {
return disc;
}
public void setDisc(double disc) {
this.disc = disc;
}
@Override
public String toString() {
return "LineSegment [roadNum=" + roadNum + ", starPoint=" + starPoint
+ ", endPoint=" + endPoint + ", disc=" + disc + "]";
}
}
ShortPath类:
package com.tangbo;
import java.util.ArrayList;
public class ShortPath {
private ArrayList points;//路径是由点构成的
private double disc;//距离
public ShortPath() {
super();
points = new ArrayList();
}
public ShortPath(Point point) {
points = new ArrayList();
points.add(point);
this.disc=ConfigurationFiles.FLAG;
}
public ArrayList getPoints() {
return points;
}
public void setPoints(ArrayList points) {
this.points = points;
}
public double getDisc() {
return disc;
}
public void setDisc(double disc) {
this.disc = disc;
}
public void addNode(Point parent) {
if(points==null)
points = new ArrayList();
points.add(0, parent);
}
public void addWeight(double desc) {
if(desc==ConfigurationFiles.FLAG)
{
disc = ConfigurationFiles.FLAG;
}else
{
disc= disc+desc;
}
}
public void print() {
System.out.println("开始点");
for(int i=0;i
package com.tangbo;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.Map;
import com.mongodb.DBCursor;
import com.mongodb.DBObject;
import com.mongodb.util.JSON;
public class Dijkstra{
public ArrayList map=null;//图
public ArrayList pointCollection = new ArrayList();;//顶点集
public ArrayList bluePoints = null;//还未加入的点
public ArrayList currentShortPaths = null;//存放目前的所有的最短路径集合
public int count=0;
public Map pointIndex = new HashMap();//建立点的索引,用来判断一个点是否已经加入顶点集
public Map roadIndex = new HashMap();//建立路段索引,用来判断两条路是否连接
public void iniMap() {
//我的所有路段是存在MongoDB里面,我需要把数据读出来,然后把地图初始化
map = new ArrayList();
pointIndex = new HashMap();
String json = "{MapID:\"605751\"}";
DBCursor dbCursor = ConfigurationFiles.mongoDB4CRUDRoadInformation.getCollections().find((DBObject)JSON.parse(json));
//DBCursor dbCursor = ConfigurationFiles.mongoDB4CRUDRoadInformation.getCollections().find();
System.out.println("dbCursor:"+dbCursor.count());
while(dbCursor.hasNext())
{
DBObject dbObject = dbCursor.next();
ArrayList pointsTemp= Util.getTrajectoryByDBObject(dbObject);
LineSegment lineSegment = new LineSegment();
Point starPoint = pointsTemp.get(0);
Point endPoint = pointsTemp.get(pointsTemp.size()-1);
lineSegment.setStarPoint(starPoint);//加入起点
lineSegment.setEndPoint(endPoint);//加入终点
double disc = Util.calcuDistByCoordinate(starPoint, endPoint);
lineSegment.setDisc(disc);//计算距离
lineSegment.setRoadNum(pointsTemp.get(0).getRoadNum());//设置路段标示
map.add(lineSegment);
addPoint(starPoint, endPoint,disc);
}
}
//判断两个点是否已经加入到顶点集中
public void addPoint(Point starPoint,Point endPoint,double disc)
{
String starPointId = starPoint.getLongitude()+""+starPoint.getLatitude();
String endPointId = endPoint.getLongitude()+""+endPoint.getLatitude();
roadIndex.put(starPointId+"#"+endPointId, disc);
if(pointIndex.get(starPointId)==null)//利用pointIndex判断这个点是否已经加入到顶点集中
{
pointCollection.add(starPoint);//将起点加入到
starPoint.setPointId(starPointId);
pointIndex.put(starPointId, pointCollection.size()-1);//然后在pointMap里面进行备注,用于快速查找
}
if(pointIndex.get(endPointId)==null)
{
pointCollection.add(endPoint);//将终点加入到
endPoint.setPointId(endPointId);
pointIndex.put(endPointId, pointCollection.size()-1);//然后在pointMap里面进行备注,用于快速查找
}
}
//Dijkstra算法开始
public ShortPath dijkstra(String startPointID,String endPointID)
{
ShortPath shortPath = null;
bluePoints = new ArrayList();//还未加入的点
currentShortPaths = new ArrayList();//存放目前已经找到的所有最短路径
//开始初始化红点集和蓝点集
System.out.println("pointCollection.size():"+pointCollection.size());
if(pointIndex.get(startPointID)!=null)
{
System.out.println("开始节点没有找到!");
System.out.println(pointCollection.get(pointIndex.get(startPointID)));
}else
{
System.out.println("没有找到!");
System.exit(0);
}
for(int i=0;i0)
{
System.out.println("bluePoints.size():"+bluePoints.size());
double minDis[][]=new double[currentShortPaths.size()][bluePoints.size()];//保存每个parent的shortpath的最后一个point与bluepoints之间的最小距离。
for(int i=0;i arrayPoints=sortPH.getPoints();
Point lastPoint=arrayPoints.get(arrayPoints.size()-1);
double dis=ConfigurationFiles.FLAG;//ConfigurationFiles.FLAG=-1,代表这个条路不同
int y=0;//用来保存bluepoint的位置
for(int j=0;j