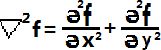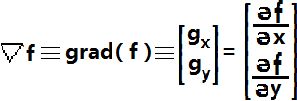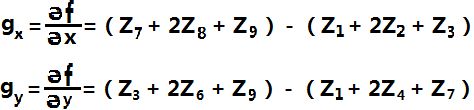【图像处理笔记】锐化空间滤波器
锐化处理的主要目的是突出灰度的过渡部分。补偿轮廓,增强图像的边缘及灰度跳变的部分,使图像变得清晰。
图像锐化的用途多种多样,应用范围从电子印刷和医学成像到工业检测和军事系统的制导等。
图像的模糊可以通过积分来实现(均值处理与积分类似)。而图像锐化,则需要微分来实现。
下面的内容,我们将讨论由数字微分来定义和实现锐化算子的方法。
图像的一阶微分二阶微分
基本上。微分算子的响应程度与图像在用算子操作的这一点的突变程度成正比,这样,图像微分增强边缘和其他突变(如噪声),而削弱灰度变化缓慢的区域。
对于一维函数f(x),其一阶微分的基本定义是差值。
这个公式是由泰勒级数推导出的。现在只须当作一个定义来接受即可。
其中,为了与二维图像函数f(x,y)的微分保持一致,我们使用了偏导符号。
对于二维函数,我们将沿着两个空间轴处理偏微分。当函数中只有一个变量时,![]() ,对于二阶微分,这也同样成立。
,对于二阶微分,这也同样成立。
我们将二阶微分定义成如下差分:
eg。一段扫描线,下面是扫描线中的灰度值
数字图像中的边缘在灰度上常常类似于斜坡过渡,如上面的例子那样,这样会导致图像的一阶微分会产生较粗的边缘,因为沿着斜坡的积分非零。
另一方面,二阶微分产生零分开的一个像素的双边缘。
由此可以得出结论,二阶微分在增强细节方面要比一阶微分好得多,这是一个适合锐化图像的理想特性。
所以我们开始主要注意二阶微分。下面,我们来考虑二维函数二阶微分的实现以及在图像锐化处理中的应用。
使用二阶微分进行图像锐化——拉普拉斯算子
基本方法是,先定义一个二阶微分的离散公式,然后构造一个基于该公式的滤波器模板,然后再把该模板与原图片卷积,从而实现锐化。
我们最关注的是一种各向同性的滤波器,这种滤波器的响应与滤波器作用的图像的突变方向无关。也就是说,各向同性滤波器是旋转不变的,即将原图像旋转之后进行滤波处理,与先对图像滤波再旋转的结果应该是相同的。
可以证明,最简单的各向同性微分算子是拉普拉斯算子。
不同的算子对应了不同的求微分的方法。
一个二维图像函数f(x,y)的拉普拉斯算子定义为
因为任意阶微分都是线性操作,所以拉普拉斯变换也是一个线性算子。为了从离散形式描述这一公式,我们使用二阶微分的公式来进行推导:
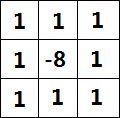
eg。滤波器模板如下:
![]()
这个滤波器可以实现拉普拉斯算子,这个模板给出了以90°为增量进行旋转的一个各向同性结果。
但其实对角线方向也可以这样组成:在数字拉普拉斯变换的定义中,在左边加入两项,即两个对角线方向各加上一个。每个新添加项的形式与![]() 类似,只是其坐标轴的方向沿着对角线的方向。
类似,只是其坐标轴的方向沿着对角线的方向。
由于每个对角线方向上的项还包含一个 -2f(x,y),所以一共应该减去8个f(x,y)
将产生如下的模板:
这个模板对45°增幅的结果是各向同性的。
由于拉普拉斯是一种微分算子,因此其应用强调的是图像中的灰度突变,并不强调灰度级缓慢变化的区域。
将原图像和拉普拉斯图像叠加在一起的简单方法,可以复原背景特性并保持拉普拉斯锐化处理的效果。
如果所使用的模板定义有负的中心系数,那么必须将原图像减去经拉普拉斯变换后的图像,而不是加上他,从而得到锐化后的结果。
![]()
由于拉普拉斯图像中即有正值又有负值,并且所有负值在显示时都被修剪为0,所以变换后的图像大部分都是黑色的。
一个典型的标定拉普拉斯图像的方法是对它的最小值加上一个新的替代0的最小值,然后将结果标定到整个灰度范围[0,L - 1]内。
opencv实现:
Mat abs, grad, dst;
Mat srcImage = imread("M:/图像处理实验/女票/灰度图.bmp");
Laplacian(srcImage, dst, CV_16S, 3, 1, 0, BORDER_DEFAULT);
//计算绝对值,并将结果转化为8位
convertScaleAbs(dst, abs);
imwrite("M:/图像处理实验/锐化空间滤波器/Laplacian.jpg", abs);
addWeighted(abs, 1, srcImage, 1, 0, dst);
imwrite("M:/图像处理实验/锐化空间滤波器/Laplacian叠加原图.jpg", dst);原图
Laplacian后的结果
Laplacian叠加原图的结果
非锐化掩蔽和高提升滤波
在印刷和出版界使用多年的图像锐化处理过程是从原图像中减去一幅非锐化(平滑过的)版本。这个称为非锐化掩蔽的处理过程由下列步骤组成:
①模糊原图像
②从原图像中减去模糊图像(产生的差值图像称为模板)
③将模板加到原图像上。
另F(x,y)表示模糊图像,非锐化掩蔽以公式形式描述如下。首先我们要先得到模板:
gmask(x,y)=f(x,y) - F(x,y)
然后在原图像上加上该模板的一个权重部分:
g(x,y)= f(x,y) + k* gmask(x,y)
通常,我们会在上式中包含一个权重系数k(k>=0)。当k=1时,我们得到上面定义的非锐化掩蔽。当k>1时,该处理称为高提升滤波。当k<1时,则不强调非锐化模板的贡献。
openCV实现:
Mat srcImage = imread("M:/图像处理实验/女票/灰度图.bmp");
Mat mediaImage, dst;
medianBlur(srcImage, mediaImage, 5);
addWeighted(mediaImage, -1, srcImage, 2, 0, dst);
imwrite("M:/图像处理实验/锐化空间滤波器/非锐化掩蔽.jpg", dst);结果:
使用一阶微分对(非线性)图像锐化——梯度
图像处理中的一阶微分是用梯度幅值来实现的。对于函数f(x,y),f在坐标(x,y)处的梯度定义为二维列向量
该向量具有重要的几何特性,即它指出了在位置(x,y)处f 的最大变化率的方向,它恰好可以反映图像边缘上的灰度变化。
可以把图像看成二维离散函数,图像梯度其实就是二维离散函数的求导。
向量![]() 的幅度值(长度)表示为M(x,y),即
的幅度值(长度)表示为M(x,y),即
它是梯度向量方向变化率在(x,y)处的值。
M(x,y)是与原图像大小相同的图像,它是当x 和y 允许在f 中的所有像素位置变化时产生的。在实践中,该图像通常称为梯度图像(或梯度)。
因为梯度向量的分量是微分,所以它们是线性算子。然而,该向量的幅度不是线性算子,因为求幅度是做平方和平方根操作。
另一方面,上面定义的梯度不是旋转不变的(各向异性),而梯度向量的幅度是旋转不变的,也就是各向同性。
在某些实现中,用绝对值来近似平方和平方根的操作更适合于计算
该表达式仍保留了灰度的相对变化,但是通常各向同性特性丢失了。然而,就像之前的拉普拉斯变换那样,在下面定义的离散梯度的各向同性仅仅在有限旋转增量的情况下被保留了,它依赖于所使用的近似微分的滤波器模板。
正如前面拉普拉斯情况下的那样,我们先对前面的公式定义一个离散的近似值,并由此形成合适的滤波器模板。
为了简化下面的讨论,我们先另中心点Z5表示任意位置(x,y)处的f(x,y),Z1表示f(x-1,y-1)
在早期的数字图像处理研究中,由Roberts提出的两个定义使用的是交叉差分:
gx = (Z9 - Z5)和 gy = (Z8 - Z6)
我们计算梯度图像为:
M(x,y) = [ (Z9 - Z5)^2 + (Z8 - Z6)^2 ] ≈ |gx| + |gy| = |Z9 - Z5| + |Z8 - Z6|
式中所需的偏微分项,可以用如下的两个滤波器模板来实现
这两个模板称为罗伯特交叉梯度算子。
用罗伯特梯度算子运算的实质就是交叉地求对角线方向像素灰度差的和。
eg。
Roberts微分算子,模板小,计算量小;但是由于模板的尺寸是2*2的,待处理的像素不能放在模板的中心,不方便计算。
我们感兴趣的最小模板是3*3的。
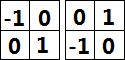
所以我们把Roberts算子改造成了一个3*3的模板,提出了以下的计算方法:
用以下模板可以实现上式
这两个模板称为Soble算子。中心系数使用权重2的思想是通过突出中心点的作用而达到平滑的目的。所有的模板中的系数和为零,这正如微分算子的期望值那样,表明灰度恒定区域的响应为0。
Soble主要是一个用于边缘检测的离散微分算子。它结合了高斯平滑和微分求导,被广泛用来计算图像灰度函数的近似梯度。
梯度处理常用于工业检测,不是辅助人工检测产品的缺陷,就是更为通用地作为自动检测的预处理。
using namespace cv;
Mat grad_x,grad_y;
Mat abs_grad_x, abs_grad_y, dst;
Mat srcImage = imread("M:/图像处理实验/女票/灰度图.bmp");
Sobel(srcImage, grad_x, CV_16S, 1, 0, 3, 1, 1, BORDER_DEFAULT);
convertScaleAbs(grad_x, abs_grad_x);
Sobel(srcImage, grad_y, CV_16S, 1, 0, 3, 1, 1, BORDER_DEFAULT);
convertScaleAbs(grad_y, abs_grad_y);
imwrite("M:/图像处理实验/锐化空间滤波器/X方向Sobel.jpg", grad_x);
imwrite("M:/图像处理实验/锐化空间滤波器/Y方向Sobel.jpg", grad_y);
//计算数组加权和
addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0, dst);
imwrite("M:/图像处理实验/锐化空间滤波器/整体Sobel.jpg", dst);
addWeighted(dst, 1, srcImage, 1, 0, dst);
imwrite("M:/图像处理实验/锐化空间滤波器/整体Sobel叠加原图.jpg", dst);x轴
y轴
整体
叠加原图后的结果
居然把女票给处理成这个样子。。O(∩_∩)O哈哈~
这也证明了前面的一个结论,二阶微分在增强细节方面要比一阶微分好得多。确实,实现二阶微分的拉普拉斯算子实现的锐化效果要比实现一阶微分的Soble算子的锐化效果要好~
以上就是锐化空间滤波器的一些知识的推导和总结~
美好是因为相信!加油~