《算法导论》第22章——基本的图算法

  虽然写这个博客主要目的是为了给我自己做一个思路记忆录，但是如果你恰好点了进来，那么先对你说一声欢迎。我并不是什么大触，只是一个菜菜的学生，如果您发现了什么错误或者您对于某些地方有更好的意见，非常欢迎您的斧正！

图的搜索指的是系统化地跟随图中的边来访问图中的每个结点。

22.1图的表示

权重图：图中的每条边都带有一个相关的权重的图。
该权重值通常由一个w：E→R的权重函数给出。
例如，设G=（V，E）为一个权重图，其权重函数为w，我们可以直接将边（u，v）∈E的权重值w（u，v）存放在结点u的邻接链表里。

边（u，v）表示结点u、v组成的一条边。

邻接链表的缺陷：无法快速判断一条边（u，v）是否在图中。
办法：在邻接链表Adj[u]里面搜索结点v。

邻接矩阵的表示：（如果结点1与结点5之间有边，则（1,5）这个地方填入1）

邻接矩阵表示权重的方法：把1替换成权重就可以了。

不论是有向图还是无向图，邻接链表表示法的存储空间需求均为θ(V+E)。
不管一个图有多少条边，邻接矩阵的空间需求均为θ(V²)。
V是顶点数，E是顶点组成的边的数量。

表示图的属性

v.d表示结点v的属性d
(u,v).f表示边(u,v)的属性f

22.2广度优先搜索

广度优先搜索是最简单的图搜索算法之一。

广度优先搜索在概念上将每个结点涂上白色、灰色、黑色。
白色：没有被发现
灰色：已知和未知的中间
黑色：所有与黑色结点邻接的结点都已经被发现

属性u.color：结点u的颜色
属性u.π：结点u的前驱（如果u没有前驱结点（没被发现），u.π=NULL）
属性u.d：计算出的从源结点s到结点u之间的距离

1、s入队
队列中：s
2、保存s，s出队，对s链表中（s->r->w）每个数进行判断
队列中：
3、r入队，w入队
队列中：r->w
4、保存w，w出队，对w链表中（w->s->t->u）每个数进行判断
队列中：r
5、t入队，x入队
队列中：r->t->x
6、保存x，x出队，对x链表中（x->w->t->u）每个数进行判断
队列中：r->t
7、u入队，y入队
队列中：r->t->u->y
8、保存y，y出队，对y链表中（y->x–>u）每个数进行判断
队列中：r->t->u
9、没有入队
队列中：r->t->u
10、然后依次u、t出队，最后r的时候又检索到一个v，最后全部出队，循环结束

最短路径

边数最少，或者加权总数最小的路径δ(s,v)。
如果最短路径不存在，则为∞。记为δ(s,v)=∞

广度优先树

打印从源结点s到结点v的一条最短路径上的所有结点

22.3深度优先搜索

深度优先搜搜总是对最近才发现的结点v的出发边进行探索，直到该结点的所有出发边都被发现为止。一旦结点v的所有出发边都被发现，搜索就“回溯”到v的前驱结点，来搜索该前驱结点的出发边。

没发现一个结点v，将v的前驱属性v.π设置为u。

深度优先搜索的前驱子图形成一个由多棵深度优先树构成的深度优先森林，森林Eπ中的边仍然称为树边。

深度优先搜索算法在每个结点上盖一个时间戳。
第一个时间戳v.d：记录结点v第一次被发现的时间（涂上灰色的时候）
第二个时间戳v.f：记录搜索树完成对v的邻接链表扫描的时间（涂上黑色的时候）

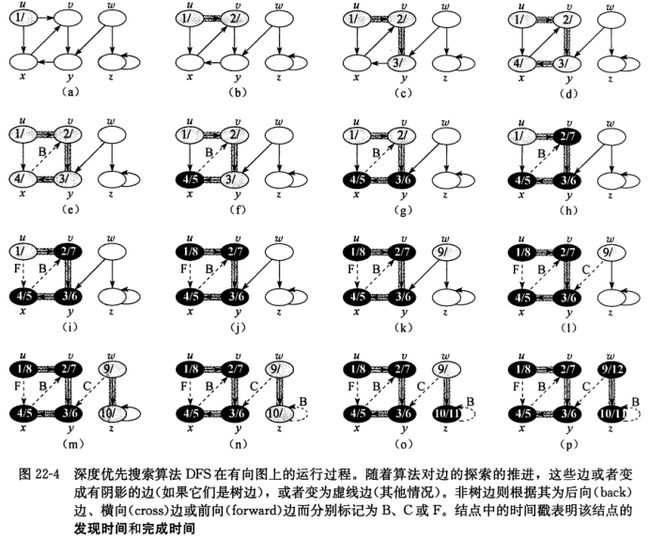
我的总结：
广度搜索：每次找到一个点，就找到它的所有能达到的点
深度搜索：每次找到一个点，就一直沿着它能达到的点找下去，找不到了就返回换一个方向。

深度优先搜索的性质

1、生成的前驱子图Gπ是由多棵树组成的森林
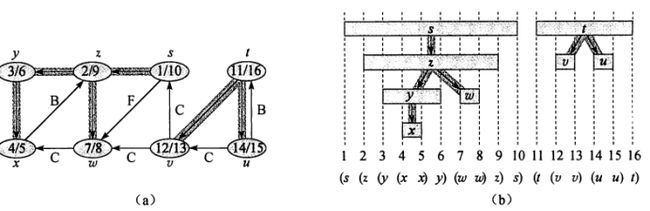
2、结点的发现时间和完成时间具有所谓的括号化性质

22.4拓扑排序

这一节阐述使用深度优先搜索来对有向无环图进行拓扑排序。
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。（摘自百度百科）
对于一个有向无环图G=（V，E），其拓扑排序是G中所有结点的一种线性排序。

22.5强连通分量

强连通分量：u->v存在，v->u存在，就是可以相互到达。或者有u->v->w->v，这样形成一个回路，也是强联通分量。简单地说，就是可以构成一个环。

这一节真心看不懂
①为什么两次深度搜索后就可以得到解，
②为什么要对图进行转置，
③做完这些后是怎么得到解的？
希望有了解的大佬能够科普我一下。感激不尽。

代码部分（建议粘贴到编辑器自己运行一下）：

广度优先搜索.h

#pragma once
#define VN 8/*点的数量*/

/*点的颜色*/
enum VerColor
{
	WHITE,	/*白色*/
	GRAY,	/*灰色*/
	BLACK	/*黑色*/
};
/*点*/
typedef struct Vertex
{
	char data;		/*点的名字*/
	VerColor color;	/*点的颜色*/
	Vertex* π;		/*点的前驱*/
	Vertex* Adj[VN];/*每个点连接的其它点*/
	int d;			/*源结点s到这个点的最短距离*/
}Vertex;

/*图*/
typedef struct Graph
{
	Vertex* V[VN];
}Graph;

/*队列*/
typedef struct Queue
{
	int tail;/*队列中最后一个数据*/
	Vertex* Q[VN];/*队列主体*/
}Queue;
/*判断队列是否为空*/
bool IsEmpty(Queue* &queue);
/*入队*/
void EnQueue(Queue* &queue, Vertex* x);
/*出队*/
Vertex* DeEnqueue(Queue* &queue);
/*广度优先搜索*/
void BFS(Graph* &G, Vertex* s);
/*广度优先树*/
void BFCpath(Vertex* s, Vertex* v);
/*测试函数*/
void TestBFS();

广度优先搜索.cpp

#include "广度优先搜索.h"
#include
#include
#include
using namespace std;

/*判断队列是否为空*/
bool IsEmpty(Queue* &queue)
{
	return queue->tail == 0;
}
/*入队*/
void EnQueue(Queue* &queue,Vertex* x)
{
	queue->Q[queue->tail] = x;
	queue->tail++;/*队列里元素个数+1*/
}
/*出队*/
Vertex* DeEnqueue(Queue* &queue)
{
	if (IsEmpty(queue))
		return NULL;
	else
	{
		queue->tail--;
		return queue->Q[queue->tail];
	}
}
/*广度优先搜索*/
void BFS(Graph* &G, Vertex* s)
{
	Vertex* u = new Vertex();
	Vertex* v = new Vertex();
	int i;

	for (i = 0; i < VN; i++)/*初始化*/
	{
		u = G->V[i];
		u->color = WHITE;
		u->d = 100;/*无穷大*/
		u->π = NULL;
	}

	s->color = GRAY;/*源结点初始化*/
	s->d = 0;
	s->π = NULL;

	Queue* q = new Queue();
	q->tail = 0;

	cout << s->data << "(" << s->d << ") ";
	EnQueue(q, s);
	while (!IsEmpty(q))
	{
		u = DeEnqueue(q);
		for (i = 0; i < VN; i++)
		{
			v = u->Adj[i];
			if (v&&v->color == WHITE)
			{
				v->color = GRAY;
				v->d = u->d + 1;
				v->π = u;
				cout << v->data <<"("<d<< ") ";
				EnQueue(q, v);
			}
		}
		u->color = BLACK;
	}
}

/*广度优先树*/
void BFCpath(Vertex* s, Vertex* v)
{
	if (v == s)
		cout << s->data << " ";
	else if (v->π == NULL)
		cout << "No path" << endl;
	else
	{
		BFCpath(s, v->π);
		cout << v->data << " ";
	}
}
/*测试函数*/
void TestBFS()
{
	Vertex* s = new Vertex(); s->data = 's';
	Vertex* r = new Vertex(); r->data = 'r';
	Vertex* v = new Vertex(); v->data = 'v';
	Vertex* t = new Vertex(); t->data = 't';
	Vertex* u = new Vertex(); u->data = 'u';
	Vertex* w = new Vertex(); w->data = 'w';
	Vertex* x = new Vertex(); x->data = 'x';
	Vertex* y = new Vertex(); y->data = 'y';
	s->Adj[0] = r;s->Adj[1] = w;
	r->Adj[0] = s; r->Adj[1] = v;
	t->Adj[0] = w; t->Adj[1] = x; t->Adj[2] = u;
	u->Adj[0] = t; u->Adj[1] = x; u->Adj[2] = y;
	v->Adj[0] = r;
	w->Adj[0] = s; w->Adj[1] = t; w->Adj[2] = x;
	x->Adj[0] = w; x->Adj[1] = t; x->Adj[2] = u; x->Adj[3] = y;
	u->Adj[0] = x; y->Adj[1] = u;
	Graph* G = new Graph();
	G->V[0] = s;
	G->V[1] = r;
	G->V[2] = t;
	G->V[3] = u;
	G->V[4] = v;
	G->V[5] = w;
	G->V[6] = x;
	G->V[7] = y;

	BFS(G, s);

	cout << endl;
	cout << endl;
	cout << "打印从s到y的路径" << endl;
	BFCpath(s, y);
}

主函数

#include "广度优先搜索.h"
#include 

int main()
{
	TestBFS();
	getchar();
	getchar();
	return 0;
}

运行结果

深度优先搜索.h

#pragma once
#define DFCN 6/*顶点的个数*/

/*颜色*/
enum DFC_COLOR
{
	DWHITE,
	DGRAY,
	DBLACK
};
/*顶点*/
typedef struct DFCV
{
	char data;/*数据*/
	int d;/*第一次被访问的时候*/
	int f;/*记录邻接结点被访问完成的时候*/
	DFC_COLOR color;/*颜色*/
	DFCV* π;/*前驱结点*/
	DFCV* next[3];/*记录它能到达的点*/
}DFCv;

typedef struct DFCG
{
	DFCv* V[DFCN];/*记录每个顶点*/
}DFCg;

/*深度优先搜索*/
void DFC(DFCg* &G);
/*遍历函数*/
void DfcVisit(DFCg* &G, DFCv* u);

/*打印时间戳*/
void DFCprint(DFCg* &G);

/*测试函数*/
void TestDFC();

深度优先搜索.cpp

#include "深度优先搜索.h"
#include
#include
#include
using namespace std;

int time = 0;/*time应该设为全局变量！注意！*/

/*深度优先搜索*/
void DFC(DFCg* &G)
{
	int i = 0;
	//int time;
	DFCv* u = new DFCv();

	for (i = 0; i < DFCN; i++)/*初始化过程*/
	{
		u = G->V[i];
		u->color = DWHITE;
		u->π = NULL;
	}
	
	time = 0;
	
	for (i = 0; i < DFCN; i++)/*对每个结点进行遍历*/
	{
		u = G->V[i];
		if (u->color == DWHITE)
			DfcVisit(G, u);
	}
}
/*遍历函数*/
void DfcVisit(DFCg* &G, DFCv* u)
{
	int i;
	DFCv* v = new DFCv();

	time++;
	u->d = time;
	u->color = DGRAY;

	for (i = 0; i < 3; i++)
	{
		v = u->next[i];/*v是u可以直接达到的点*/
		if (v&&v->color == DWHITE)/*如果v存在且v的颜色为白色*/
		{
			v->π = u;/*设定v的前驱*/
			DfcVisit(G, v);/*对v继续深入搜索*/
		}
	}
	u->color = DBLACK;/*此时已经搜索完u的邻接链表了，所以置为黑色*/
	time++;
	u->f = time;/*结束时间*/
}
/*打印时间戳*/
void DFCprint(DFCg* &G)
{
	for (int i = 0; i < DFCN; i++)
	{
		cout << G->V[i]->data << "  (" << G->V[i]->d << "/" << G->V[i]->f << ")" << endl;
	}
	cout << endl;
}
/*测试函数*/
void TestDFC()
{
	DFCv* u = new DFCv(); u->data = 'u';
	DFCv* v = new DFCv(); v->data = 'v';
	DFCv* w = new DFCv(); w->data = 'w';
	DFCv* x = new DFCv(); x->data = 'x';
	DFCv* y = new DFCv(); y->data = 'y';
	DFCv* z = new DFCv(); z->data = 'z';
	u->next[0] = v; u->next[1] = x;
	v->next[0] = y;
	w->next[0] = y; w->next[1] = z;
	x->next[0] = v;
	y->next[0] = x;
	z->next[0] = z;

	DFCg* G = new DFCg();
	G->V[0] = u;
	G->V[1] = v;
	G->V[2] = w;
	G->V[3] = x;
	G->V[4] = y;
	G->V[5] = z;

	DFC(G);
	DFCprint(G);
}

主函数

#include "深度优先搜索.h"
#include 

int main()
{
	TestDFC();
	getchar();
	getchar();
	return 0;
}

运行结果