Matlab机器人工具箱（2-2）：一些demo（工作空间计算）

参考：
https://blog.csdn.net/Kalenee/article/details/81990130
https://blog.csdn.net/qq_23670601/article/details/100094905
机器人的工作空间是机器人在运转过程中,手部参考点在空间所能达到的点的集合。工作空间是一种重要的运动学指标，常用于衡量机器人活动范围，机器人无法到达处于工作空间以外的目标。机器人的工作空间的种类有三种，分别是全工作空间，可达工作空间和灵巧工作空间，本文中计算的是机器人给定所有位姿时，末端可到达目标点的集合，即全工作空间。

01 数值法

这里采用数值法进行机器人全工作空间的绘制，具体流程如下图所示。首先是设置各关节角度限制，然后以某一步距值对各关节分别进行累加并计算正解获得末端点位置，当各关节都到达最大限制角度后停止计算，最后对获得的所有末端点进行处理绘制出机器人的边界曲线，根据这些边界曲线可以绘制出代表机器人的工作空间的边界曲面。

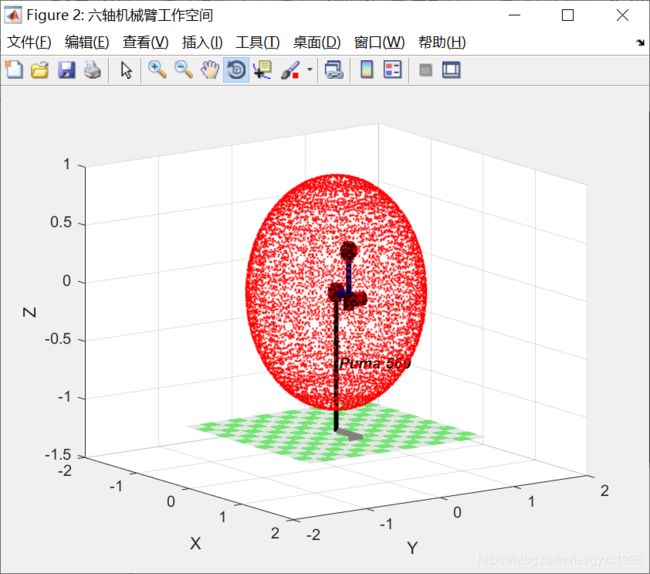
%六轴机械臂工作空间计算
clc;
clear;
format short;%保留精度
 
%角度转换
du=pi/180;  %度
radian=180/pi; %弧度
 
%% 模型导入
mdl_puma560
 
%% 求取工作空间
    %关节角限位
    q1_s=-180; q1_end=180;
    q2_s=0;    q2_end=90;
    q3_s=-90;  q3_end=90;
    q4_s=-180; q4_end=180;
    q5_s=-90;  q5_end=90;
    q6_s=0;    q6_end=360;
    
    %设置step
    %step越大，点越稀疏，运行时间越快
    step=20;%计算步距
    step1= (q1_end -q1_s) / step;
    step2= (q2_end -q2_s) / step;
    step3= (q3_end -q3_s) / step;
    step4= (q4_end -q4_s) / step;
    step5= (q5_end -q5_s) / step;
    step6= (q6_end -q6_s) / step;
    
    %计算工作空间
    tic;%tic1
    i=1;
    T = zeros(3,1);
    T_x = zeros(1,step1*step2*step3*step4*step5);
    T_y = zeros(1,step1*step2*step3*step4*step5);
    T_z = zeros(1,step1*step2*step3*step4*step5);  
    for  q1=q1_s:step:q1_end
        for  q2=q2_s:step:q2_end
              for  q3=q3_s:step:q3_end
                  for  q4=q4_s:step:q4_end
                      for q5=q5_s:step:q5_end
                              T=p560.fkine([q1*du q2*du q3*du q4*du q5*du 0]);%正向运动学仿真函数
                              T_x(1,i) = T(1,4); 
                              T_y(1,i) = T(2,4); 
                              T_z(1,i) = T(3,4); 
                              i=i+1;
                      end
                 end
             end
        end 
    end
    disp(['循环运行时间：',num2str(toc)]); 
    t1=clock;
     
%% 绘制工作空间
figure('name','六轴机械臂工作空间')
hold on
plotopt = {'noraise', 'nowrist', 'nojaxes', 'delay',0};
p560.plot([0 20*du 0 0 0 0], plotopt{:});
plot3(T_x,T_y,T_z,'r.','MarkerSize',3);
disp(['绘制工作空间运行时间：',num2str(etime(clock,t1))]);  
 
%获取X,Y,Z空间坐标范围
Point_range=[min(T_x) max(T_x) min(T_y) max(T_y) min(T_z) max(T_z)]
hold off

02 蒙特卡罗法

蒙特卡罗方法（英语：Monte Carlo method），也称统计模拟方法，是1940年代中期由于科学技术的发展和电子计算机的发明，而提出的一种以概率统计理论为指导的数值计算方法。是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。

使用蒙特卡罗法计算工作空间相较于数值化，优势在于用时较短，以100000个点为例，用时在2到3分钟内（根据关节运动范围和关节数不同而不同）
劣势在于蒙特卡罗方法只能趋近于结果而不能完全得到真实的结果，但经过测试，只要数据的数量足够大，也能获得较为准确的结果。

蒙特卡罗法一般实现步骤

1. 用蒙特卡罗方法模拟某一过程时，需要产生各种概率分布的随机变量。
2. 用统计方法把模型的数字特征估计出来，从而得到实际问题的数值解。

蒙特卡罗法工作空间求解步骤

1. 产生各关节的随机变量
2. 计算正解

clc;
clear;
 
%% 准备
    %保留精度
    format short;
    
    %角度转换
    du=pi/180;  %度
    radian=180/pi; %弧度
    
    %模型导入
    mdl_puma560
 
%% 参数
    %关节角限位
    q1_s=-180; q1_end=180;
    q2_s=0;    q2_end=90;
    q3_s=-90;  q3_end=90;
    q4_s=-180; q4_end=180;
    q5_s=-90;  q5_end=90;
    q6_s=0;    q6_end=360;
    
    %计算点数
    num=100000;
 
%% 求取工作空间
    %设置轴关节随机分布,轴6不对工作范围产生影响，设置为0
    q1_rand = q1_s + rand(num,1)*(q1_end - q1_s);%rand产生num行1列，在0~1之间的随机数
    q2_rand = q2_s + rand(num,1)*(q2_end - q2_s);
    q3_rand = q3_s + rand(num,1)*(q3_end - q3_s);
    q4_rand = q4_s + rand(num,1)*(q4_end - q4_s);
    q5_rand = q5_s + rand(num,1)*(q5_end - q5_s);
    q6_rand = rand(num,1)*0;
    q = [q1_rand q2_rand q3_rand q4_rand q5_rand q6_rand]*du;
    
    %正运动学计算工作空间
    tic;
    T_cell = cell(num,1);
    for i=1:1:num
        [T_cell{i}]=p560.fkine(q(i,:));%正向运动学仿真函数
    end
    %[T_cell{:,1}]=p560.fkine(q);%正向运动学仿真函数
    disp(['运行时间：',num2str(toc)]);
 
 %% 分析结果
    %绘制工作空间
    t1=clock;
    figure('name','机械臂工作空间')
    hold on
    plotopt = {'noraise', 'nowrist', 'nojaxes', 'delay',0};
    p560.plot([0 30*du 0 0 40*du 0], plotopt{:});
     figure_x=zeros(num,1);
     figure_y=zeros(num,1);
     figure_z=zeros(num,1);
     for cout=1:1:num
         figure_x(cout,1)=T_cell{cout}(1,4);
         figure_y(cout,1)=T_cell{cout}(2,4);
         figure_z(cout,1)=T_cell{cout}(3,4);
     end
     plot3(figure_x,figure_y,figure_z,'r.','MarkerSize',3);
     hold off
     disp(['绘制工作空间运行时间：',num2str(etime(clock,t1))]);  
     
     %获取X,Y,Z空间坐标范围
     Point_range=[min(figure_x) max(figure_x) min(figure_y) max(figure_y) min(figure_z) max(figure_z)];