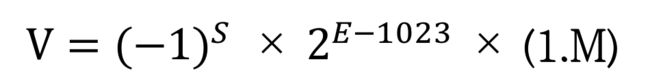前言:
在看了 JavaScript 浮点数陷阱及解法 和 探寻 JavaScript 精度问题 后,发现没有具体详细的推导0.1+0.2=0.30000000000000004的过程,所以我写了此文补充下
正文:
console.log(0.1+0.2) //0.30000000000000004
将 0.1 转为二进制:
没有整数部分
小数部分为 0.1,乘 2 取整,直至没有小数:
0.1 * 2 = 0.2 ...0
0.2 * 2 = 0.4 ...0
0.4 * 2 = 0.8 ...0
0.8 * 2 = 1.6 ...1
0.6 * 2 = 1.2 ...1
//开始循环
0.2 * 2 = 0.4 ...0
。。。
。。。
0.1 的二进制为:0.0 0011 0011 0011 无限循环0011
采用科学计数法,表示 0.1 的二进制:
//0.00011001100110011001100110011001100110011001100110011 无限循环0011
//由于是二进制,所以 E 表示将前面的数字乘以 2 的 n 次幂
//注意:n 是十进制的数字,后文需要
2^(-4) * (1.1001100110011循环0011)
(-1)^0 * 2^(-4) * (1.1 0011 0011 0011 循环0011)
由于 JavaScript 采用双精度浮点数(Double)存储number,所以它是用 64 位的二进制来存储 number 的
十进制与 Double 的相互转换公式如下:
V:表示十进制的结果
SEM:表示双精度浮点数的结果(就是 S 拼 E 拼 M,不是相加)
2^(-4) * (1.1001100110011循环0011)套用此公式右边,得:
(-1)^0 * 2^(-4) * (1.1 0011 0011 0011 循环0011)
所以,
S = 0 //二进制
E = 1019 //十进制
M = 1001100110011循环0011 //二进制
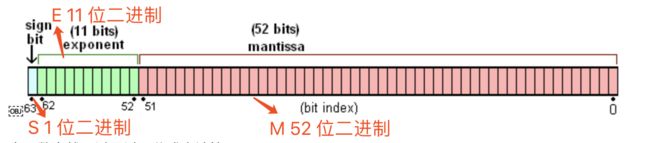
双精度浮点数 存储结构如下:
由图可知:
①
S 表示符号位,占 1 位
E 表示指数位,占 11 位
M 小数位,占 52 位(如果第 53 位为 1,需要进位!)
②
//二进制
S = 0 满足条件
//十进制
E = 1019 不满足条件,需要转为 11 位的二进制
//二进制
M = 1001100110011循环0011 不满足条件,需要转为 52 位的二进制
① 将 1019 转为 11 位的二进制
//1019
1111111011 ,共 10 位,但 E 要 11 位,所以要在首部补 0
E = 01111111011
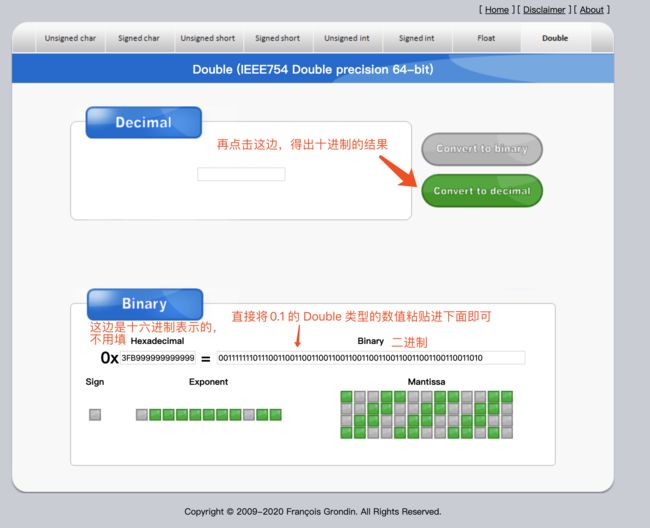
在线转换工具:在线转换工具(BigNumber时不准确)
② 将1001100110011循环0011转为 52 位的二进制
//1 0011 0011 0011 循环0011 第53位
1 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011
第 53 位为 1,要进位,同时舍去第53位及其往后的
M = 1001100110011001100110011001100110011001100110011010 //共 52 位
综上:
S = 0
E = 01111111011
M = 1001100110011001100110011001100110011001100110011010
拼接 SEM 得到 64 位双精度浮点数:
S E M
0 01111111011 1001100110011001100110011001100110011001100110011010
//合并得到 64 位双精度浮点数
0011111110111001100110011001100110011001100110011001100110011010
故 0.1 在 JavaScript 中存储的真实结构为:
0011111110111001100110011001100110011001100110011001100110011010
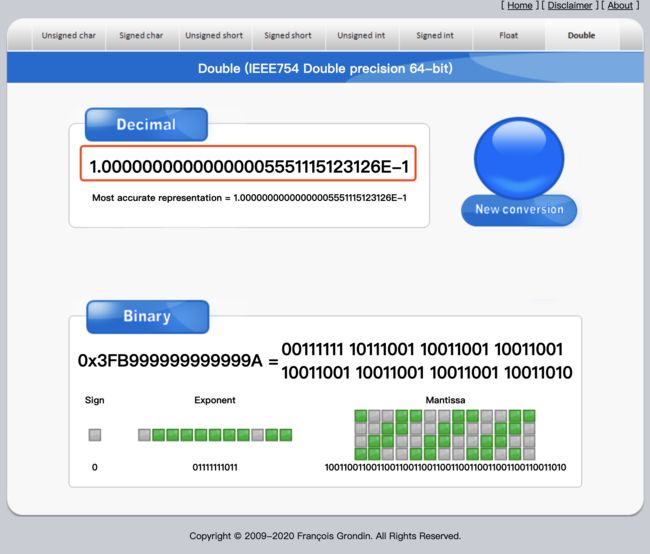
通过 Double相互转换十进制(它是我找得到的有效位数最多的网站) 得:
1.00000000000000005551115123126E-1
等于
1.00000000000000005551115123126 * (10^-1)
等于
0.100000000000000005551115123126
也就是说:
0.1 //十进制
相当于
(-1)^0 * 2^(-4) * (1.1001100110011001100110011001100110011001100110011010) //十进制的值
相当于
0011111110111001100110011001100110011001100110011001100110011010 //Double(双精度)
相当于
0.100000000000000005551115123126 //十进制!
所以用一句话来解释为什么JS有精度问题:
简洁版:
因为JS采用Double(双精度浮点数)来存储number,Double的小数位只有52位,但0.1等小数的二进制小数位有无限位,所以当存储52位时,会丢失精度!
考虑周到版:
因为JS采用Double(双精度浮点数)来存储number,Double的小数位只有52位,但除最后一位为5的十进制小数外,其余小数转为二进制均有无限位,所以当存储52位时,会丢失精度!
验证下Double值0011111110111001100110011001100110011001100110011001100110011010是否等于十进制0.100000000000000005551115123126:
根据十进制与 Double 的相互转换公式得:
//V = (-1)^S * 2^(E-1023) * (1.M)
//S = 0
//E = 119
//M = 1001100110011001100110011001100110011001100110011010
V = (-1)^0 * 2^(-4) * (1.1001100110011001100110011001100110011001100110011010)
//1.1001100110011001100110011001100110011001100110011010的 Double 值计算过程
//S = 0
//E = 1023,二进制为 01111111111
//M = 1001100110011001100110011001100110011001100110011010
//SEM=0011111111111001100110011001100110011001100110011001100110011010
//转为十进制:1.60000000000000008881784197001E0
= 0.0625 * 1.60000000000000008881784197001
用 BigInt 类型来相乘:
625n * 160000000000000008881784197001n
等于
100000000000000005551115123125625n
加上小数点后 33 位,等于
0.100000000000000005551115123125625
发现是四舍五入后的结果,也就是一样的
0.100000000000000005551115123126
结果一致,验证正确!
同理,将 0.2 转为二进制(过程略,轮到你来练练手了):
0011 0011 0011 无限循环 0011
Double:
//注意第 53 位是 1,需要进位!
(-1)^0 * 2^(-3) * (1. 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010)
S = 0
E = 1020,二进制为 01111111100
M = 1001100110011001100110011001100110011001100110011010
SEM = 0011111111001001100110011001100110011001100110011001100110011010
通过 Double相互转换十进制(它是我找得到的有效位数最多的网站) 得:
2.00000000000000011102230246252E-1
等于
0.200000000000000011102230246252
也就是说:
0.2 //十进制
相当于
(-1)^0 * 2^(-3) * (1.1001100110011001100110011001100110011001100110011010) //十进制的值
相当于
0011111111001001100110011001100110011001100110011001100110011010 //Double(双精度)
相当于
0.200000000000000011102230246252 //十进制!
用 BigInt 类型来相加:
100000000000000005551115123126n + 200000000000000011102230246252n
等于
300000000000000016653345369378n
加上小数点一位
0.300000000000000016653345369378
等等!好像不等于0.30000000000000004?
0.30000000000000001 6653345369378保留小数点后 17 位得:
0.30000000000000001
再次验证:
0.1 = (-1)^0 * 2^(-4) * (1.1001100110011001100110011001100110011001100110011010)
= 0.00011001100110011001100110011001100110011001100110011010
0.2 = (-1)^0 * 2^(-3) * (1.1001100110011001100110011001100110011001100110011010)
= 0.0011001100110011001100110011001100110011001100110011010
0.00011001100110011001100110011001100110011001100110011010 +
0.0011001100110011001100110011001100110011001100110011010 =
0.01001100110011001100110011001100110011001100110011001110
两者相加,结果为:
0.01 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 10
转化为 Double,即 SEM:
(-1)^0 * 2^(-2) * (1.0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0100 )
S = 0
E = 1021,二进制为 01111111101
最后的 10 被舍掉,并且进位
M = 0011001100110011001100110011001100110011001100110100
SEM = 0011111111010011001100110011001100110011001100110011001100110100
通过 Double相互转换十进制(它是我找得到的有效位数最多的网站) 得:
3.00000000000000044408920985006E-1
等于
0.30000000000000004 4408920985006
保留小数点后 17 位得:
0.30000000000000004
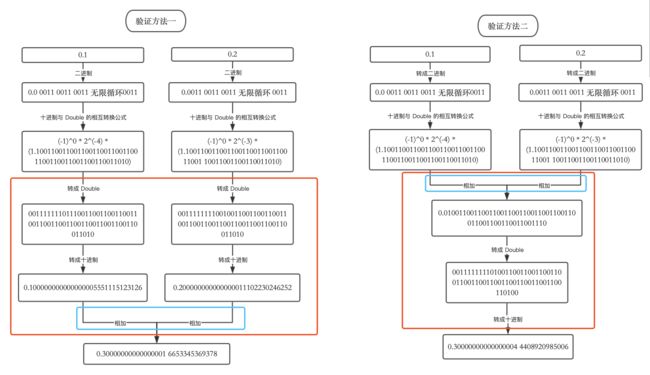
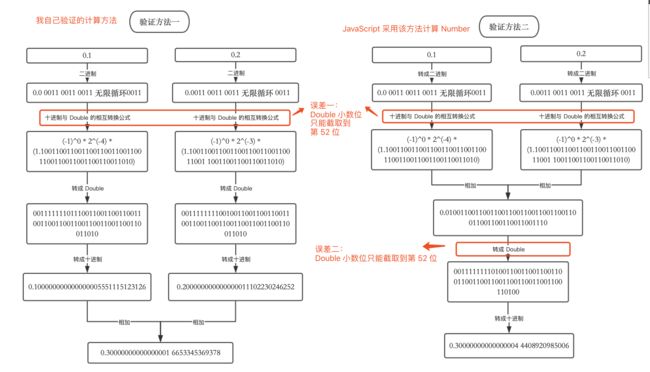
可以看到,两种不同的计算过程,导致了计算结果的偏差,我制作了一张流程图帮助大家理解:
显然,JavaScript 是按照「验证方法二」去计算 0.1+0.2 的值的,我有两个疑问:
① 为什么不用误差更小的「验证方法一」呢?
这个我暂时不知道,有大佬知道的话麻烦给我留言。。
② 为什么「验证方法二」的结果误差比较大?
蹊跷在 二进制小数相加转成 Double 的过程 上,也就是舍去 53 位,并进位会导致误差:
进位后的 SEM
SEM = 0011111111010011001100110011001100110011001100110011001100110100
转为十进制
V = 0.300000000000000044408920985006
如果不进位的话
SEM = 0011111111010011001100110011001100110011001100110011001100110011
转为十进制
V = 0.299999999999999988897769753748
发现还是对不上「验证一」的结果,原因还是在于 Double 的小数位只能保留到 52 位,截取超出的位数不可避免地会导致误差,并且较大!
网上找的关于0.1+0.2=0.30000000000000004的文章都是写的「验证方法二」,我也不知道自己的「验证方法一」是否有错误,恳请看到的读者加以指正。
问题 ② 算解决了,问题 ① 暂不解决,我太累了。。
最后:
感谢你的耐心看完了这篇文章,麻烦给文中参考的文章点个赞,没有他们也不会有这篇文章的诞生,谢谢!
(完)