jzoj5336 【NOIP2017提高A组模拟8.24】提米树 （dfs序dp，奇异姿势dp）

题面

分析

剪枝的意思就是你可以任意选点作为叶子。（前提是他子树不选）
比赛的时候有一种60分的n^2 log n做法，就是在dfs序上直接dp.
但是正解比较奇怪，先画颗树出来看看，就会发现根到真·叶子的路径上有且只有一个被选为叶子。于是我们考虑设一种玄学的dp。 令 f[i] 为在dfs序上，当前最后一个叶子选的是i的最大价值。
想想能更新i的点有哪些。 由于要保证每条到叶子的路径上都有选中的，那么当前状态要么没有意义（ 选他的祖先 ），要么就从相邻的叶子节点到二者lca （不含）这条路径上的点更新过来。 （看不懂的就看图吧）

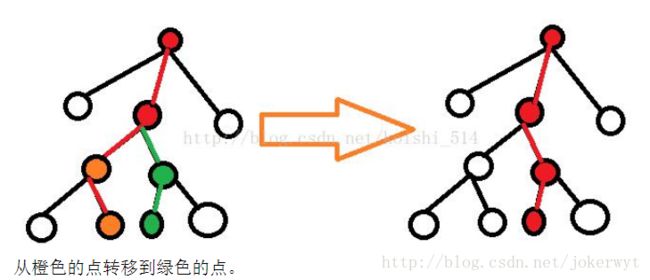
这样每次枚举两个相邻叶子，然后暴力枚举从哪个绿点转移的话是O(n^2)的。
没有被转移到的点价值就是本身。 （因为他不需要接盘，只选自己就行）

在优化之前，先证明一个结论： 相邻叶子节点的路径长度（也就是点数-1）不会超过2n.
考虑一条边会被选到多少次，当然最多两次了，子树外到内 与 内到外各一次。子树内都选不到他。

这样从上到下更新要更新的点，lca~当前要更新的点 的路径mx当然是递增的，然后左边决策集合中的mx也是递增的，维护一个指针now表示当前决策集合（按深度排序，感受一下） 1..now-1是用自己那边的mx,然后now..lca是用 lca~当前要更新的点上的mx。
这样维护一个前缀和+后缀和，快速计算一下两部分的最优值就可以O(n)做了。 （细节比较多但为什么有大佬能打进1000byte）

Demo

#include 
#include 
#include 
#define max(a,b) ((a)<(b)?(b):(a))
#define min(a,b) ((a)<(b)?(a):(b))
using namespace std;
const int N=1e5+10,INF=2e9;
int final[N],nex[N],to[N],tot,dep[N];
int n,a[N];
int fa[N],ch[N];

int f[N];
int s[N],td[N],pre[N],sufmxa[N],sufmxf[N];
int tmp[N];

void link(int x,int y) {to[++tot]=y, nex[tot]=final[x], final[x]=tot;}
void dfs(int x) {
    dep[x]=dep[fa[x]]+1;
    if (!final[x]) ch[++ch[0]]=x; else
    for (int i=final[x]; i; i=nex[i]) fa[to[i]]=x, dfs(to[i]);
}
int init(int x,int y) {
    int tx=x,ty=y,g=0;
    s[0]=td[0]=0;
    while (dep[ty]>dep[x]) td[++td[0]]=ty,ty=fa[ty];
    while (dep[tx]>dep[y]) {
        if (f[tx]==f[0]) f[tx]=a[tx];
        s[++s[0]]=tx;
        tx=fa[tx];
    }
    while (tx!=ty) {
        if (f[tx]==f[0]) f[tx]=a[tx];
        td[++td[0]]=ty, s[++s[0]]=tx;
        tx=fa[tx],ty=fa[ty];
    }
    s[++s[0]]=g=tx;
    pre[0]=sufmxa[s[0]]=sufmxf[s[0]]=-INF;
    if (f[g]==f[0]) f[g]=a[g]; 
    for (int i=s[0]-1; i; i--) {
        sufmxf[i]=max(sufmxf[i+1],f[s[i]]);  //max  f[a..g]
        sufmxa[i]=max(sufmxa[i+1],a[s[i+1]]);//max  a[fa[a]..g]
    }
    for (int i=1; i0]; i++) pre[i]=max(pre[i-1],f[s[i]] - sufmxa[i]); //max ans[1..i]
    return g;
}
int main() {
    freopen("3.in","r",stdin);
//  freopen("3.out","w",stdout);
    cin>>n;
    for (int i=1; i<=n; i++) {
        int k=0;
        scanf("%d %d",&a[i],&tmp[0]);
        for (int j=1; j<=tmp[0]; j++) scanf("%d",&tmp[j]);
        for (int j=tmp[0]; j; j--) link(i,tmp[j]);
    }
    memset(f,128,sizeof f);
    dfs(1);
    for (int i=1; i0]; i++) {
        int x=ch[i],y=ch[i+1],g=init(x,y),now=s[0],rmx=0;
        for (int d,j=td[0]; j; j--) {
            d=td[j], rmx=max(rmx,a[fa[d]]);
            while (now>1 && sufmxa[now-1]<=rmx) now--;
            f[d]=max(pre[now-1], sufmxf[now] - rmx)+a[d];
        }
    }

    int ans=0;
    for (int i=ch[ch[0]]; i; i=fa[i]) {
        if (f[i]==f[0]) f[i]=a[i];
        ans=max(ans,f[i]);
    }
    printf("%d\n",ans);

}