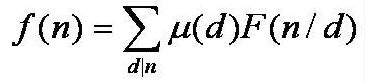三个启发性连接：
http://blog.csdn.net/lixuepeng_001/article/details/50577932
http://www.cnblogs.com/femsub/p/5723780.html
http://blog.csdn.net/acdreamers/article/details/8542292
GCD
Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 10964 Accepted Submission(s): 4142
Problem Description
Given 5 integers: a, b, c, d, k, you're to find x in a...b, y in c...d that GCD(x, y) = k. GCD(x, y) means the greatest common divisor of x and y. Since the number of choices may be very large, you're only required to output the total number of different number pairs.
Please notice that, (x=5, y=7) and (x=7, y=5) are considered to be the same.
Yoiu can assume that a = c = 1 in all test cases.
Input
The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 3,000 cases.
Each case contains five integers: a, b, c, d, k, 0 < a <= b <= 100,000, 0 < c <= d <= 100,000, 0 <= k <= 100,000, as described above.
Output
For each test case, print the number of choices. Use the format in the example.
Sample Input
2 1 3 1 5 1 1 11014 1 14409 9
Sample Output
Case 1: 9 Case 2: 736427
Hint
For the first sample input, all the 9 pairs of numbers are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 5), (3, 4), (3, 5).
Source
2008 “Sunline Cup” National Invitational Contest
莫比乌斯函数
这里简述一下莫比乌斯函数：
若d=1 那么μ(d)=1
若d=p1p2…pr （r个不同质数，且次数都为一）μ(d)=(-1)^r
其余 μ(d)=0
即μ[i]=1表示i是偶数个不同素因子的乘积，μ[i]=-1表示i是奇数个不同素因子的乘积，μ[i]=0表示其他（即如果有相同素因子就是0）
而i==1时，规定μ[1] = 1。
莫比乌斯反演的性质
性质一：（莫比乌斯反演公式）
f(n)=∑(d|n)μ(d)F(n/d)
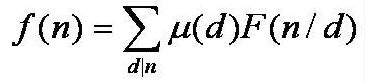
性质二：μ(n)是积性函数
性质三：设f是算术函数，它的和函数F(n)=∑(d|n)f(d)是积性函数，那么f也是积性函数。
题意：从[1...n]和[1..m]中取一对（x，y）使得gcd(x,y)==k，k,n,m已知。
思路：这里可以转化一下，也就是[1,n/k],[1,m/k]之间互质的数的个数
设F(n)为公约数为n的组数个数 ，即 F（d）为 有多少对（x,y）满足 gcd（x,y）== d 的倍数 。
f(n)为最大公约数为n的组数个数，即 f（d）为有多少对（x,y）满足 gcd（x,y）== d 。
注意以下(a|b)指能被a整除的b;
F(n)=∑(n|d)f(d)
所以有：
f(n)=∑(n|d)μ(d/n)F(d)
你发现F(x)能求出是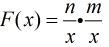 
(n=b / k，m=d / k) (莫比乌斯的关键就是F(x)能算数得出，因为它是得到答案的必须条件)
那么其实我们需要解决的就剩下如何求出 f（1）是多少的问题了。
根据公式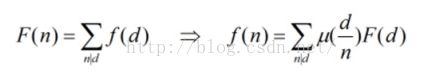
你可以发现，在你对函数进行题设时是需要满足反演对函数的要求的，这个需要你自己来体会，至于另一个公式的设法是 “约数” 的关系，而这个则是 “倍数” 的关系。
那么问题就基本上解决了，f（1）= mu（1）*F（1）+ mu（2）*F（2）+…… 这个式子的终止条件是什么呢？很显然在所限定的区间内，d最大为 min（m,n）。
那么完整的式子就应该是 f（1）= mu（1）*F（1）+ mu（2）*F（2）+……mu（min（m,n））*F（min（m,n））。至此 这道题目就顺利的解决了。
mu 函数打表即可。
不过这里需要注意去重，题目中说明了，（1，2）和（2，1）算一种情况，那么我们就要减去多余了的情况，怎那么找出那些多算进去的情况呢？ 下面的图画的很清楚：
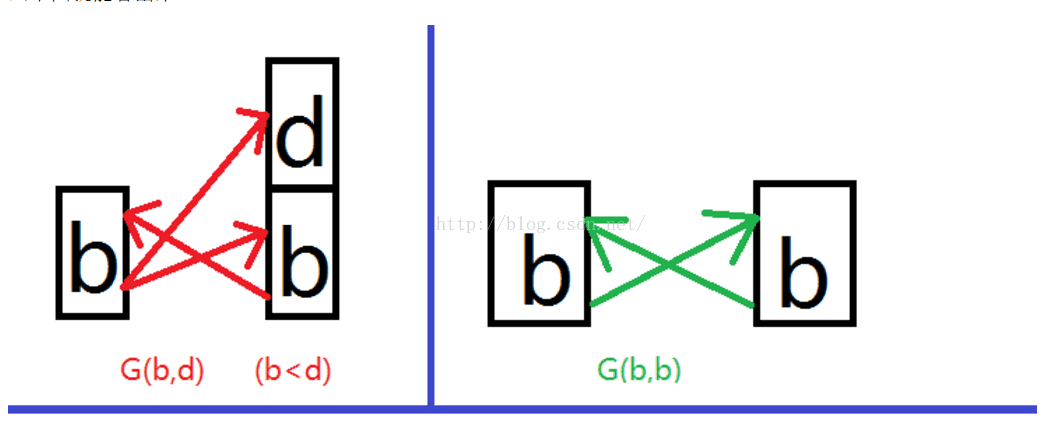
G（b,b）就是多算进去的这些情况，（把每个满足条件的(x,y)对想象成的图的边。那么所有的双向边都需要去掉一条）
那么 G（b，d）- G（b，b）/ 2 就是最终我们要求的结果了。（上图为借鉴）
#include
