浅谈二次剩余
本文只讨论p为奇质数的情况
下面大量内容借用神仙yyc大佬的blogs
才不是因为我懒
概(che)论(dan)
给 c , p c, p c,p求解
x 2 ≡ c ( m o d p ) x^2 \equiv c \pmod p x2≡c(modp)
前置芝士
欧拉判别法
首先要知道这个数有没有二次剩余,即 x 2 ≡ c ( m o d p ) x^2 \equiv c \pmod p x2≡c(modp)是否有解
先给出结论: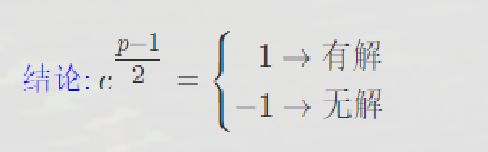
证明: 把 c p − 1 2 平 方 一 下 变 成 c ( p − 1 2 ) 2 = c p − 1 = 1 ( 根 据 费 马 小 定 理 , 所 以 开 根 后 为 ± 1 把c^{\frac{p-1}{2}}平方一下变成c^{{(\frac{p-1}{2})}^2} = c^{p-1}=1(根据费马小定理,所以开根后为±1 把c2p−1平方一下变成c(2p−1)2=cp−1=1(根据费马小定理,所以开根后为±1
当 c p − 1 2 = − 1 时 可 以 用 反 证 法 把 x 2 = c 代 入 得 到 x p − 1 ≡ − 1 ( m o d p ) 显 然 和 费 马 小 定 理 矛 盾 当c^{\frac{p-1}{2}}=-1时可以用反证法把x^2=c代入得到x^{p-1}\equiv-1(mod \ p) 显然和费马小定理矛盾 当c2p−1=−1时可以用反证法把x2=c代入得到xp−1≡−1(mod p)显然和费马小定理矛盾
或者可以直接简单理解一下如果 c p − 1 2 = − 1 c^{\frac{p-1}{2}}=-1 c2p−1=−1说明是在原根环的一个偶数点的位置上,那么必定存在一个位置平方是这个偶数位置
二次剩余个数
p − 1 2 个 \large \frac{p-1}{2}个 2p−1个
引 理 : c 2 ≡ ( p − c ) 2 ( m o d p ) , 就 相 当 于 c 2 和 ( − c ) 2 引理:c^2 \equiv (p-c)^2 \pmod p,就相当于c^2和(-c)^2 引理:c2≡(p−c)2(modp),就相当于c2和(−c)2
我 们 定 义 一 个 奇 怪 的 东 西 : ( a p ) 表 示 上 面 那 个 东 西 又 叫 勒 让 德 符 号 ( l e g e n d r e s y m b o l ) 我们定义一个奇怪的东西:\large ( \frac{a}{p}) 表示上面那个东西 \ \ \ 又叫 勒让德符号 (legendre symbol) 我们定义一个奇怪的东西:(pa)表示上面那个东西 又叫勒让德符号(legendresymbol)

有下列性质:
( a b p ) = ( a p ) ( b p ) \large ( \frac{ab}{p})=\large ( \frac{a}{p})\large ( \frac{b}{p}) (pab)=(pa)(pb)
( q p ) ( p q ) = ( − 1 ) p − 1 2 ∗ q − 1 2 \large ( \frac{q}{p})\large ( \frac{p}{q})=(-1)^{\frac{p-1}{2} * \frac{q-1}{2}} (pq)(qp)=(−1)2p−1∗2q−1
其实还是挺容易理解的
算法流程
假 设 我 们 要 求 n 在 模 p 意 义 下 的 二 次 剩 余 , 即 x 2 ≡ n ( m o d p ) , 求 x 假设我们要求n在模p意义下的二次剩余,即x^2 \equiv n \pmod p,求x 假设我们要求n在模p意义下的二次剩余,即x2≡n(modp),求x
先 随 机 一 个 值 a 使 得 ( a 2 − n ) p − 1 2 = − 1 , 也 就 是 说 a 2 − n 不 是 p 的 二 次 剩 余 。 先随机一个值a使得 (a^2-n)^{\frac{p-1}{2}}=-1,也就是说a^2-n不是p的二次剩余。 先随机一个值a使得(a2−n)2p−1=−1,也就是说a2−n不是p的二次剩余。
因为上面说了有 p − 1 2 \frac{p-1}{2} 2p−1个,所以期望 2 2 2次就能随机到
然 后 我 们 强 行 将 其 开 根 , 这 样 会 得 到 一 个 类 似 虚 数 的 东 西 , 准 确 来 说 时 设 w 2 = ( a 2 − n ) , 学 过 F F T 的 应 该 都 能 理 解 然后我们强行将其开根,这样会得到一个类似虚数的东西,准确来说时设w^2=(a^2-n),学过FFT的应该都能理解 然后我们强行将其开根,这样会得到一个类似虚数的东西,准确来说时设w2=(a2−n),学过FFT的应该都能理解
可以证明扩系后仍然是环。
引 理 : ( a + b ) p = a p + b p 引理:(a+b)^p = a^p + b^p 引理:(a+b)p=ap+bp
证明直接二项式展开一下再加上Lucas就好了,详细过程可以看yyc的blog
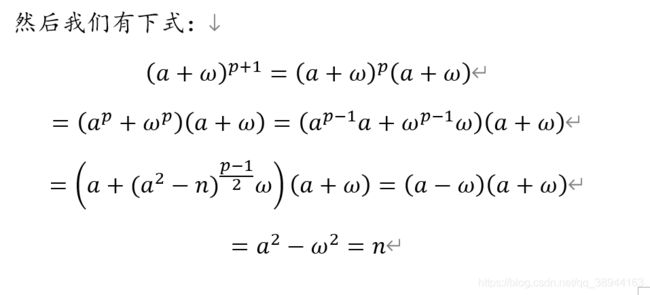
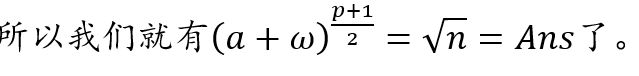
所以这么随便搞搞就好了
#includeto be continue……