PID控制的MATLAB仿真（2）对PID控制的一些改进

1. 积分分离

为了解决在大误差情况下积分器积累的大控制量影响系统超调的情况，可以只在误差较小的时候开启积分项，以消除静差；在误差大的情况下取消积分项。
我们设定一个阈值，在这个阈值的范围内开启积分项，在误差大的时候使用PD控制；在误差小的时候使用PID控制，提高精度。
对阈值的选择在这里比较重要，首先可以获得无积分情况的稳态误差，阈值需要包含误差带。如果不能包含误差带，也就是说一直无法开启积分消除静差，积分起不到作用了。

具体方法1：先进行无积分的阶跃信号下的仿真，获得稳态误差。阈值β为误差乘以一个略大于一的系数
下面的就是按照这种思路进行的。(程序输入阶跃信号最后必须接近稳定，否则参数不可用)
(方法2：对线性系统，通过计算得到无积分情况下的稳态误差。比如使用终值定理。)

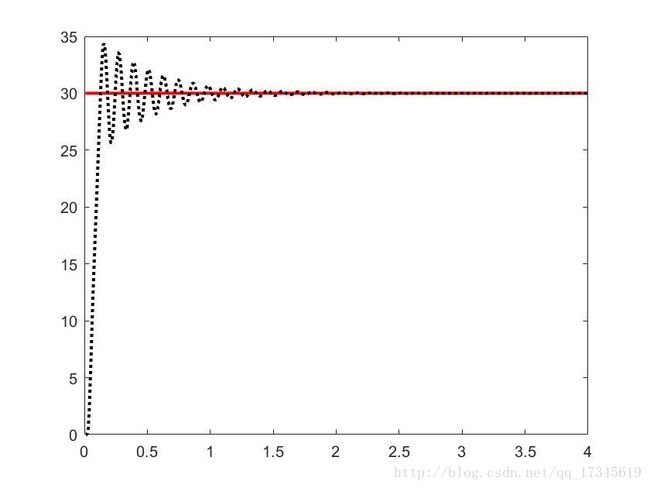
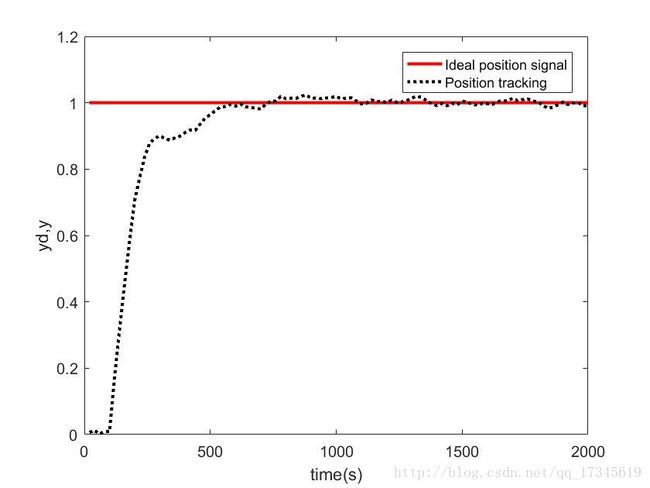
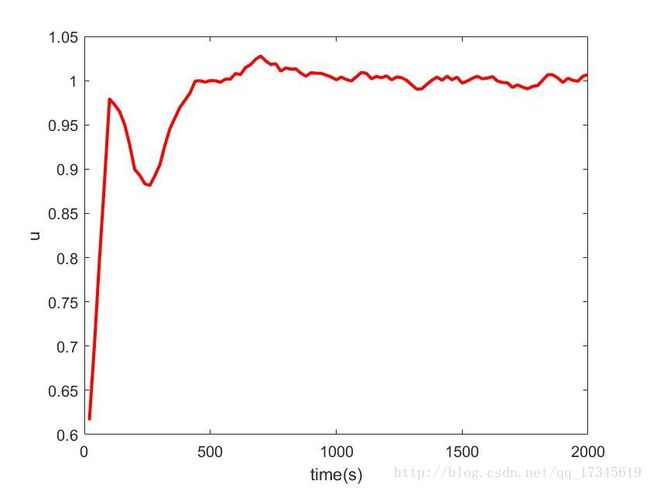
不加入积分分离：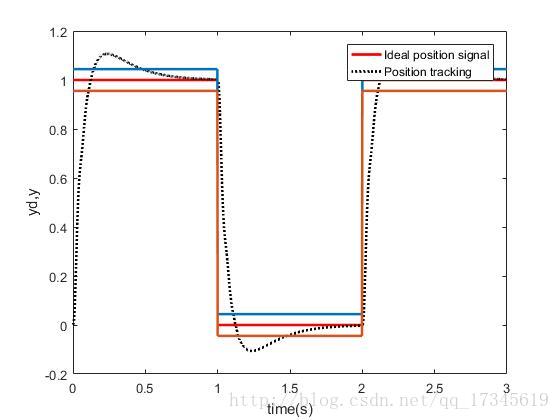

自动确定阈值的积分分离：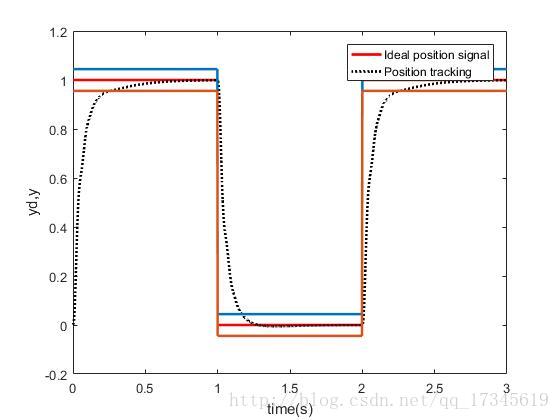

可见通过积分分离减少了超调，并且稳态精度也很好。
上面的积分分离相对而言是一种比较粗糙的做法，如果把积分的突然分离换成一种渐变，效果则要好一些。

---

2. 抗积分饱和

受到各种实际系统的约束，控制器的输出值只能在一个安全的范围，积分值超出线性区后保持不变，这种特性在积分值饱和后，退出饱和状态的时间较长，系统的动态特性变差。

防止积分饱和的方法之一就是抗积分饱和法，该方法的思路是在计算u(k)时，首先判断上一时刻的控制量u(k-1)是否已经超出了极限范围：如果u(k-1)大于umax，则只累加负偏差;如果 u(k-1)小于umin，则只累加正偏差。从而避免控制量长时间停留在饱和区。

不加入抗积分饱和：

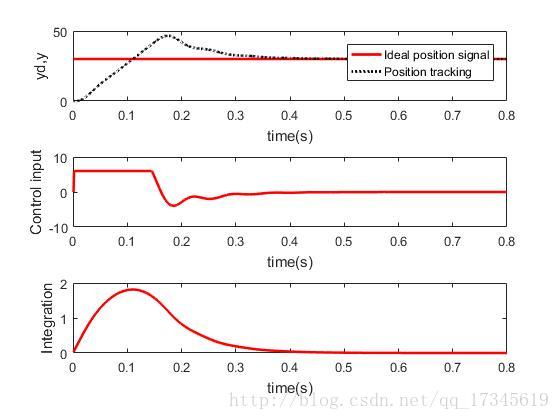
加入抗积分饱和：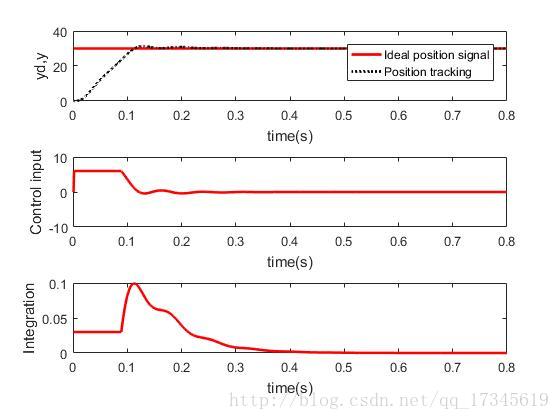

控制器输出值最大设定为6，可见由积分器造成的超调被减弱了。

---

3. 梯形积分

运用梯形公式，使用两次采样值计算每步的累加值。
将原来的积分运算:

∫t0e(t)dt=∑i=0ke(i)T

替换为：

∫t0e(t)dt=∑i=0ke(i)+e(i−1)2T

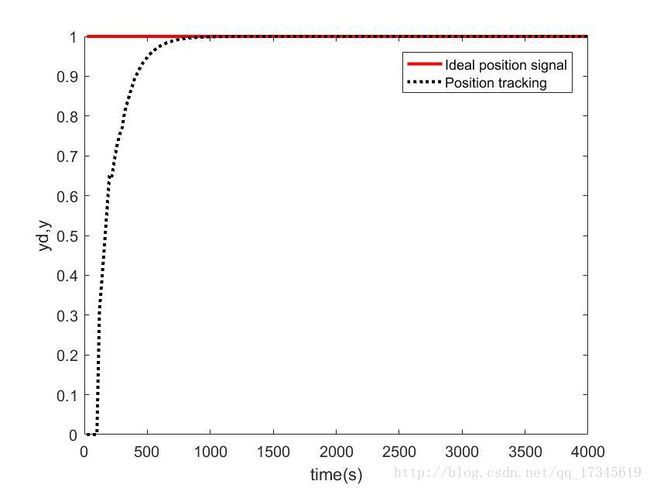
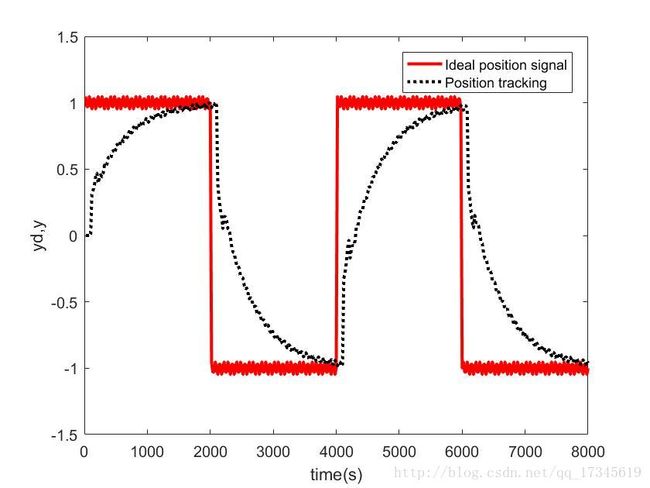
感觉在采样足够的情况下效果差异不明显，在采样比较稀疏的情况下控制效果有较大提升。
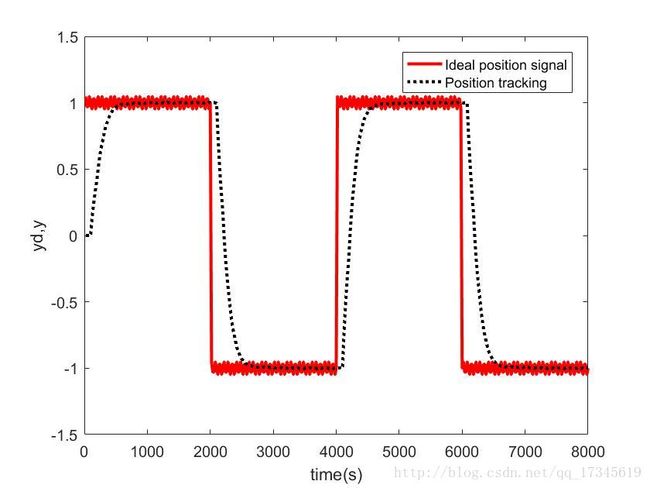
在采样足够大情况下：

采样较少使用普通积分的输出响应：

采样较少使用梯形积分后：

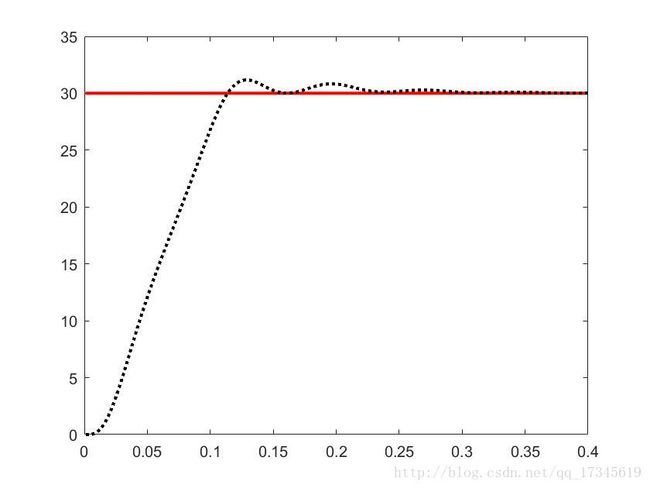
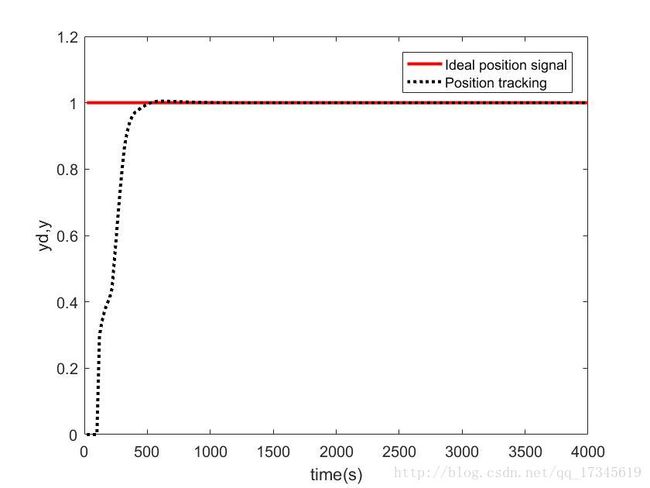
4. 变速积分

将上面的积分分离算法进一步优化，使得在偏差较小时开启较大的积分系数，在偏差较小时使用较小的积分系数，减少积分项对系统动态调节过程的影响，同时又保证了偏差较快收敛。
其中积分项为：

∫t0e(t)f(e(t))dt=∑i=0ke(i)f(i)T

可见积分分离算法是变速积分的一种特例，即

f(i)={1,0,|e(i)|<=max|e(i)|>max

变速积分系数f 可以取线性关系，

f(i)=⎧⎩⎨⎪⎪1,A−|e(i)|+BA,0,|e(i)|<=BB<|e(i)|<=A+B|e(i)|>A+B

原系统：

使用变速积分：

5. 不完全微分

微分项的计算对噪声敏感，若系统存在噪声，可加入低通滤波器衰减噪声。
滤波器可以加在微分上，也可以加在整个PID调节器上。
系统响应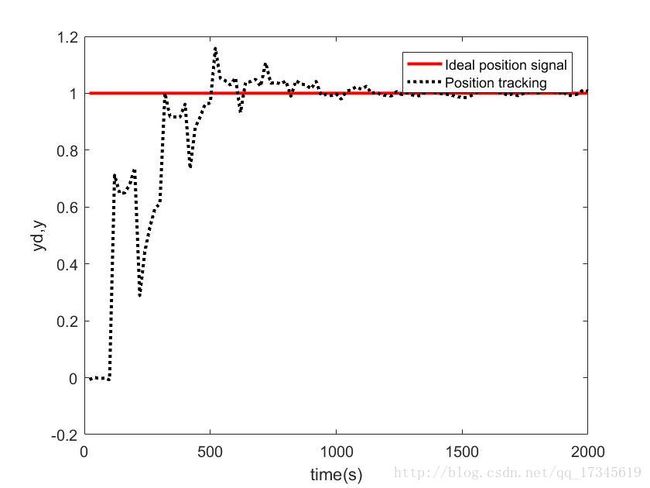

控制器输出

加入滤波器
系统响应

控制器输出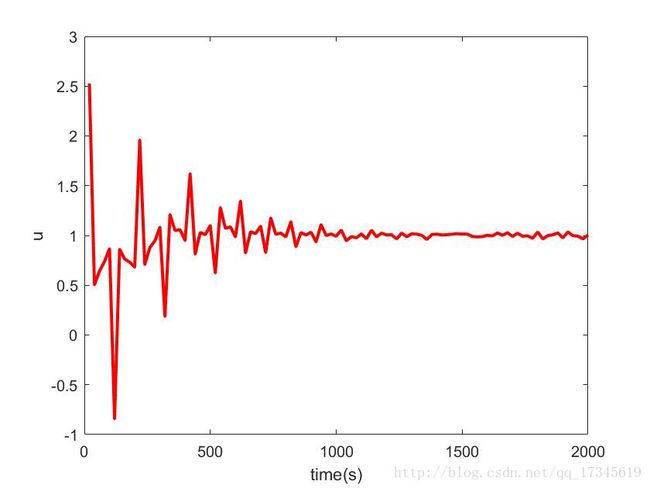

6. 微分先行

当给定信号突变时，系统容易发生震荡，为了避免这种情况，可以对微分项进行改进。

原系统跟踪方波信号：

采用微分先行结构：

7. 带死区

经常会出现这种情况，受到传感器、执行器精度的限制，在给定值附近系统会频繁动作，比如电机的轻微抖动，为了消除这种现象，可以人为的加入一段不灵敏区域，在这段区域内不进行调节。

e(k)={0,e(k),|e(k)|<=|e0||e(k)|>|e0|

8. 带前馈补偿

如果知道控制对象较为精确的模型，加入前馈环节可以使得前馈环节与被控对象传递函数之积为1。系统性能可以大大提高

9. 带Kerman滤波器

---

%% 自动确定分离阈值的带积分分离的PID控制器
% 阈值确定的思路：获得无积分情况的稳态误差，阈值β包含误差带。
% 具体方法1：先进行无积分的阶跃信号下的仿真，获得稳态误差。阈值β为误差乘以一个略大于一的系数
% (具体方法2：对线性系统，通过计算得到无积分情况下的稳态误差。)
% 程序输入阶跃信号最后必须接近稳定，否则参数不可用
%参考先进pid一书
clear all;
close all;

ts=0.0001;
tim=3;
kp=0.5;ki=2;kd=0.01;
kbeta=1.2;
%输入信号类型 -1方波 0阶跃 1三角波 2锯齿波 3随机
S=-1;  
% 模型
sys=tf(5.235e005,[1,87.35,1.047e004,10000]);
dsys=c2d(sys,ts,'z');
[num,den]=tfdata(dsys,'v');

u_1=0.0;u_2=0.0;u_3=0.0;
yd_1=rand;
y_1=0;y_2=0;y_3=0;

x=[0,0,0]';
error_1=0;

for k=1:1:tim/ts
time(k)=k*ts; 
yd(k)=1;
u(k)=kp*x(1)+kd*x(2);   %PD Controller

%Restricting the output of controller
if u(k)>=10
   u(k)=10;
end
if u(k)<=-10
   u(k)=-10;
end

%Linear model
y(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(2)*u_1+num(3)*u_2+num(4)*u_3;
error(k)=yd(k)-y(k);

yd_1=yd(k);

u_3=u_2;u_2=u_1;u_1=u(k);
y_3=y_2;y_2=y_1;y_1=y(k);

x(1)=error(k);                %Calculating P
x(2)=(error(k)-error_1)/ts;   %Calculating D
x(3)=x(3)+error(k)*ts;        %Calculating I
xi(k)=x(3);

error_1=error(k);
D=0;
if D==1  %Dynamic Simulation Display
    plot(time,yd,'b',time,y,'r');
    pause(0.00000000000000000);
end
end
% 阈值
beta=kbeta*abs(x(1))



u_1=0.0;u_2=0.0;u_3=0.0;
yd_1=rand;
y_1=0;y_2=0;y_3=0;

x=[0,0,0]';
error_1=0;

for k=1:1:tim/ts
time(k)=k*ts;



if S==-1   %square Signal
    if k<=tim/ts/3     
       yd(k)=1;
    end
    if k>tim/ts/3 && k<=2*tim/ts/3
       yd(k)=0;
    end
    if k>2*tim/ts/3 && k<=3*tim/ts/3
       yd(k)=1;
    end
      % yd(k)=1;
end
if S==0   %step Signal
       yd(k)=1;
end
if S==1   %Triangle Signal
   if mod(time(k),2)<1     
       yd(k)=mod(time(k),1);
    else
       yd(k)=1-mod(time(k),1);
    end
       yd(k)=yd(k)-0.5;
end
if S==2   %Sawtooth Signal
   yd(k)=mod(time(k),1.0);
end
if S==3   %Random Signal
    yd(k)=rand;  
    dyd(k)=(yd(k)-yd_1)/ts;  %Max speed is 5.0
    while abs(dyd(k))>=5.0
    yd(k)=rand;  
        dyd(k)=abs((yd(k)-yd_1)/ts);
    end
end
%积分分离
if abs(x(1))>beta
    x(3)=0;
end
u(k)=kp*x(1)+kd*x(2)+ki*x(3);   %PID Controller

%Restricting the output of controller
if u(k)>=10
   u(k)=10;
end
if u(k)<=-10
   u(k)=-10;
end

%Linear model
y(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(2)*u_1+num(3)*u_2+num(4)*u_3;
error(k)=yd(k)-y(k);

yd_1=yd(k);

u_3=u_2;u_2=u_1;u_1=u(k);
y_3=y_2;y_2=y_1;y_1=y(k);

x(1)=error(k);                %Calculating P
x(2)=(error(k)-error_1)/ts;   %Calculating D
x(3)=x(3)+error(k)*ts;        %Calculating I
xi(k)=x(3);

error_1=error(k);
if D==1  %Dynamic Simulation Display
    plot(time,yd,'b',time,y,'r');
    pause(0.00000000000000000);
end
end

figure(1);
plot(time,yd,'r',time,y,'k:',time,yd+ones(size(time))*beta,time,yd-ones(size(time))*beta,'linewidth',2);
xlabel('time(s)');ylabel('yd,y');
legend('Ideal position signal','Position tracking');
figure(2);
plot(time,yd-y,'linewidth',2);
xlabel('time(s)');ylabel('yd-y');
legend('error');

---

%抗积分饱和

%PID Controler with intergration sturation
clear all;
close all;

ts=0.001;
sys=tf(5.235e005,[1,87.35,1.047e004,0]);
dsys=c2d(sys,ts,'z');
[num,den]=tfdata(dsys,'v');

u_1=0.0;u_2=0.0;u_3=0.0;
y_1=0;y_2=0;y_3=0;

x=[0,0,0]';

error_1=0;

um=6;
kp=0.85;ki=9.0;kd=0.0;   
for k=1:1:800
time(k)=k*ts;

yd(k)=30;           %Step Signal
u(k)=kp*x(1)+kd*x(2)+ki*x(3);   % PID Controller

if u(k)>=um
   u(k)=um;
end
if u(k)<=-um
   u(k)=-um;
end

%Linear model
y(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(2)*u_1+num(3)*u_2+num(4)*u_3;

error(k)=yd(k)-y(k);

M=1;
if M==1  %Using intergration sturation
if u(k)>=um
   if error(k)>0
      alpha=0;
   else 
      alpha=1;
   end
elseif u(k)<=-um
   if error(k)>0
      alpha=1;
   else 
      alpha=0;
   end
else
   alpha=1;
end

elseif M==2  %Not using intergration sturation
    alpha=1;   
end

%Return of PID parameters
u_3=u_2;u_2=u_1;u_1=u(k);   
y_3=y_2;y_2=y_1;y_1=y(k);
error_1=error(k);

x(1)=error(k);                % Calculating P
x(2)=(error(k)-error_1)/ts;   % Calculating D
x(3)=x(3)+alpha*error(k)*ts;  % Calculating I

xi(k)=x(3);
end
figure(1);
subplot(311);
plot(time,yd,'r',time,y,'k:','linewidth',2);
xlabel('time(s)');ylabel('yd,y');
legend('Ideal position signal','Position tracking');
subplot(312);
plot(time,u,'r','linewidth',2);
xlabel('time(s)');ylabel('Control input');
subplot(313);
plot(time,xi,'r','linewidth',2);
xlabel('time(s)');ylabel('Integration');

%PID Controller with changing integration rate
clear all;
close all;
%Big time delay Plant
ts=20;
sys=tf([1],[60,1],'inputdelay',80);
dsys=c2d(sys,ts,'zoh');
[num,den]=tfdata(dsys,'v');

u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;
y_1=0;y_2=0;y_3=0;
error_1=0;error_2=0;
ei=0;

for k=1:1:200
time(k)=k*ts;

yd(k)=1.0;  %Step Signal

%Linear model
y(k)=-den(2)*y_1+num(2)*u_5;
error(k)=yd(k)-y(k);

kp=0.45;kd=12;ki=0.0048;
A=0.4;B=0.6;

%T type integration
ei=ei+(error(k)+error_1)/2*ts; 

M=1;
if M==1     %Changing integration rate
if abs(error(k))<=B
   f(k)=1;
elseif abs(error(k))>B&abs(error(k))<=A+B
   f(k)=(A-abs(error(k))+B)/A;
else
   f(k)=0;
end
elseif M==2  %Not changing integration rate
    f(k)=1;
end

u(k)=kp*error(k)+kd*(error(k)-error_1)/ts+ki*f(k)*ei;

if u(k)>=10
   u(k)=10;
end
if u(k)<=-10
   u(k)=-10;
end
%Return of PID parameters
u_5=u_4;u_4=u_3;u_3=u_2;u_2=u_1;u_1=u(k);   
y_3=y_2;y_2=y_1;y_1=y(k);   
error_2=error_1;
error_1=error(k);
end
figure(1);
plot(time,yd,'r',time,y,'k:','linewidth',2);
xlabel('time(s)');ylabel('yd,y');
legend('Ideal position signal','Position tracking');
figure(2);
plot(time,f,'r','linewidth',2);
xlabel('time(s)');ylabel('Integration rate f');