卡尔曼滤波器原理简介
引用知乎中的一段话:“PID和卡尔曼滤波乃是控制工程师的两大法宝。几十年过去了卡尔曼滤波在理论研究上仍然保持着活跃,研究方向包括各种非线性的,噪声统计参数未知的自适应和鲁棒滤波。更重要的是现在计算机的发展将其推向了实用化,包括各种位姿估计,多传感器信息融合,车辆导航等。”
这足以看出卡尔曼滤波在控制领域中的重要性,而本篇博客就来简要地分析一下卡尔曼滤波器的基本原理。
卡尔曼滤波器
首先,我们可以用如下这种简单的描述来简要介绍KALMAN滤波器的基本原理:
假如要对某一状态量进行估计,你有一个线性函数模型,模型的过程噪声方差阵为 Q Q Q;同时你还有一个传感器,传感器的测量噪声方差阵为 R R R;要得到对状态的准确估计该怎么做呢?很简单,对模型输出和传感器输出做一个简单的加权和即可,即 V t = ( 1 − K ) V q + K V r V_t=(1-K)V_q+KV_r Vt=(1−K)Vq+KVr;当模型的噪声较大时 K K K取大一点,当传感器的噪声较大时 K K K取小一点,即 K K K的大小决定了你应该更相信模型还是传感器;而卡尔曼滤波器的作用就是通过不断地迭代,最终得到了最优的 K K K值: K a l m a n Kalman Kalman增益即为两者的最优权值。
实际上,随着卡尔曼滤波器的不断迭代,协方差矩阵 P P P最终将会收敛,此时卡尔曼增益固定,状态更新方程变成了与一阶低通滤波相同的形式;但是,卡尔曼滤波器的性能是优于低通滤波器的,因为其在迭代过程中找到了最优滤波常数。
卡尔曼滤波器又叫做最佳线性滤波器,只能描述状态与状态之间的线性关系;
优点:
1.实现简单;
2.是一种时域的滤波方式;
3.不需要进行频域变换;
4.可以用来用作状态估计。
下面使用过一个简单的速度估计的例子来简要分析卡尔曼滤波器的原理:
状态转移
首先确定小车系统的状态如下:
x t = [ p t v t ] x_{t}=\left[\begin{array}{c}{p_{t}} \\ {v_{t}}\end{array}\right] xt=[ptvt]
进一步得到系统状态量的更新形式(基本的运动学方程,其中 u t u_t ut为加速度):
p t = p t − 1 + v t − 1 × Δ t + u t × Δ t 2 2 v t = v t − 1 + u t × Δ t \begin{array}{l}{p_{t}=p_{t-1}+v_{t-1} \times \Delta t+u_{t} \times \frac{\Delta t^{2}}{2}} \\ {v_{t}=v_{t-1}+u_{t} \times \Delta t}\end{array} pt=pt−1+vt−1×Δt+ut×2Δt2vt=vt−1+ut×Δt
写成矩阵形式:
[ p t v t ] = [ 1 Δ t 0 1 ] [ p t − 1 v t − 1 ] + [ Δ t 2 2 Δ t ] u t \left[\begin{array}{c}{p_{t}} \\ {v_{t}}\end{array}\right]=\left[\begin{array}{cc}{1} & {\Delta t} \\ {0} & {1}\end{array}\right]\left[\begin{array}{c}{p_{t-1}} \\ {v_{t-1}}\end{array}\right]+\left[\begin{array}{c}{\frac{\Delta t^{2}}{2}} \\ {\Delta t}\end{array}\right] u_{t} [ptvt]=[10Δt1][pt−1vt−1]+[2Δt2Δt]ut
即:
x ^ t − = F t x ^ t − 1 + B t u t \hat{x}_{t}^{-}=F_{t} \hat{x}_{t-1}+B_{t} u_{t} x^t−=Ftx^t−1+Btut
其中:
F t = [ 1 Δ t 0 1 ] , B t = [ Δ t 2 2 Δ ] F_{t}=\left[\begin{array}{cc}{1} & {\Delta t} \\ {0} & {1}\end{array}\right], B_{t}=\left[\begin{array}{c}{\frac{\Delta t^{2}}{2}} \\ {\Delta}\end{array}\right] Ft=[10Δt1],Bt=[2Δt2Δ]
至此便得出了系统的状态转移方程。
有了状态转移公式就可以用来推测当前的状态,但是所有的推测都是包含噪声的,噪声越大,不确定越大,可以用协方差矩阵来表示这次推测带来的不确定性。
协方差矩阵
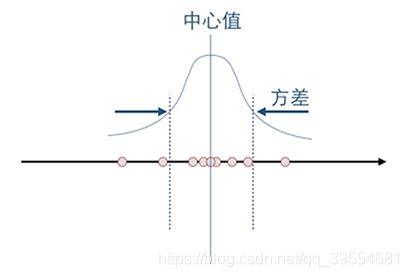
假设我们有一个一维的包含噪声的数据,这个数据每次测量都不同,单都是围绕在一个中心值的周围,那么我们可以用均值和方差来表示该数据集,这实际上是假设了改数据服从高斯分布;我们将该一维数据集投影到坐标轴上,如下图:
接下来看二维的情况,将二维的测量数据投影到坐标轴上,可以看出在两个轴上数据都服从高斯分布:
其中:
图1:两个维度的噪声独立;
图2:两个维度的噪声相关,且一个维度的噪声增大,另一个维度的噪声也增大;
图3:两个维度的噪声相关,且一个维度的噪声增大,另一个维度的噪声减小;
如果说两个维度的噪声独立,那么使用方差便可以描述这两个维度之间的关系;但是在两个维度相关情况下,方差不足以描述这种相关性,此时便要引入协方差来描述两个维度之间的相关程度;写成矩阵的形式如下:
cov ( x , x ) = [ σ 11 σ 12 σ 12 σ 22 ] \operatorname{cov}(x, x)=\left[\begin{array}{cc}{\sigma_{11}} & {\sigma_{12}} \\ {\sigma_{12}} & {\sigma_{22}}\end{array}\right] cov(x,x)=[σ11σ12σ12σ22]
对角线上的两个元素表示两个维度的方差,反对角线上的元素表示协方差;
噪声协方差矩阵的传递
如何描述协方差在状态转移中的传递呢?答案是乘以状态转移矩阵:
P t − = F P t − 1 F T P_{t}^{-}=F P_{t-1} F^{T} Pt−=FPt−1FT
即从上一时刻的协方差来推测当前时刻的协方差,这里使用到了协方差矩阵的性质:
cov ( A x , B x ) = A cov ( x , x ) B T \operatorname{cov}(A x, B x)=A \operatorname{cov}(x, x) B^{T} cov(Ax,Bx)=Acov(x,x)BT
此时我们还需要考虑一件事情,我们的预测模型并不是一定准确的,其本身也包含了过程噪声。
因此,上式写成如下形式:
P t − = F P t − 1 F T + Q P_{t}^{-}=F P_{t-1} F^{T}+Q Pt−=FPt−1FT+Q
其中协方差矩阵 Q Q Q表示预测系统带来的噪声。这个公式表示了不确定性在各个时刻之间的传递关系。
观测矩阵
H = [ 1 0 ] H=\left[\begin{array}{ll}{1} & {0}\end{array}\right] H=[10]
z t = H x t + v z_{t}=H x_{t}+v zt=Hxt+v
由于观测值也不是百分百可靠,所以引入 v v v来表示观测值的噪声;同时观测噪声的协方差矩阵用 R R R来表示。
注意:
这一步中,我们可以通过多个传感器对系统状态的不完全表述中,推断出系统的真实状态;卡尔曼滤波器的数据融合功能正是在这个测量矩阵中体现出来的。
状态更新
x ^ t = x ^ t − + K t ( z t − H x ^ t − ) \hat{x}_{t}=\hat{x}_{t}^{-}+K_{t}\left(z_{t}-H \hat{x}_{t}^{-}\right) x^t=x^t−+Kt(zt−Hx^t−)
可以看出,状态更新方程与一阶低通滤波器一致;其中, K t K_t Kt为卡尔曼增益:
K t = P t − H T ( H P t − H T + R ) − 1 K_{t}=P_{t}^{-} H^{T}\left(H P_{t}^{-} H^{T}+R\right)^{-1} Kt=Pt−HT(HPt−HT+R)−1
卡尔曼增益的推导比较复杂,此处只做定性的分析:
首先,卡尔曼增益权衡预测状态协方差P和观测协方差矩阵R的大小,来决定是相信预测模型多一点还是相信观测量多一点;相信预测模型的话,残差的权重小,相信观测量的话,残差权重大;
同时,卡尔曼增益将残差的表现形式从观察域转换到状态域(因为多数情况下,观测值的维数是要小于状态值的);即用观测值的残差来更新状态值。
扩展
根据卡尔曼增益的形式,可以看出其包含了协方差矩阵 P P P的信息;本文例子中我们实际得到的观测值是汽车的位置,卡尔曼增益利用速度和位置这两个维度之间的相关性,从位置的残差里推算出了速度的残差,从而可以使用位置信息对位置和速度均进行估计;卡尔曼滤波器实际上也可以作为一种状态观测器。
噪声协方差矩阵的更新
P t = ( I − K t H ) P t − P_{t}=\left(I-K_{t} H\right) P_{t}^{-} Pt=(I−KtH)Pt−
这一步计算出在状态更新过程中协方差矩阵的变化。
以上就是卡尔曼滤波算法的原理和整个迭代流程,卡尔曼滤波器的五条公式总结如下:
博主使用 K a l m a n Kalman Kalman进行了姿态估计的工作并进行了嵌入式的代码实现,我强烈建议大家使用 M A T L A B C o d e r MATLAB \ Coder MATLAB Coder工具箱将 M a t l a b Matlab Matlab环境下的 K a l m a n Kalman Kalman滤波器代码转成 C C C代码,该工具箱非常强大且简单实用,转换后的代码包含了矩阵求逆,矩阵转置和矩阵乘法等基本运算,避免了手写代码可能出现的错误,而且只需要少许改动就能加入到你的工程代码中去。
参考文献:
卡尔曼滤波器的原理以及在MATLAB中的实现