算法 动态连通性--如何设计和分析算法
前言
本文是对《算法》（橙色那本）动态连通性问题的学习笔记。对于该问题的解法，书本已经说得非常详细，同时也能很容易地在网上找到他们的答案（代码），而且解决该问题的数据结构，还是所有数据结构里面最简单的——数组，所以我觉得仅仅将该问题的答案（即代码）抄写上来同时作为笔记的重点并没有很大的意义。如同书中在该问题的开头所说的，大意是：我们学习这个例子，是为了学习设计和分析算法的基本方法。所以我将这篇笔记的重点都放在理解问题、分析问题、推导解法、算法分析这几个点上面。在学习完动态连通性问题后，我觉得对于算法类问题，理解问题、真正搞清楚问题的本质，比得到一个问题的解法更有意义。有时候，当你搞清楚问题的本质之后，可能已经自然而然得到该问题的答案。
提出问题
以下为算法第四版中文版的原话：
问题的输入是一列整数对，其中每个整数都表示一个某种类型的对象，一对整数p、q可以被理解为“p和q是相连的”。我们假设“相连”是一种等价关系，这也就意味着它具有：
>自反性：p和p是相连的。
>对称性：如果p和q是相连的，那么q和p也是相连的。
>传递性：如果p和q是相连的且q和r是相连的，那么p和r也是相连的。
等价关系能够将对象分为多个等价类。在这里，当且仅当两个对象相连时它们才属于同一个等价类。我们的目标是编写一个程序来过滤掉序列中所有无意义的整数对（两个整数均来自于同一个等价类中）。换句话说，当程序从输入中读取了整数对p和q时，如果已知的所有整数对都不能说明p和q是相连的，那么则将这一对整数写入到输出中。如果已知的数据可以说明p和q是相连的，那么程序应该忽略p、q这对整数并继续处理输入中的下一对整数。
类比生活，理解问题
为了更加深刻理解问题，我们将书中类比生活的几个例子展开来。
电脑与网络
假设现在有一间房，房子里面有若干台电脑，我们给它们编上号（从0到N-1，一共N台）。那么现在，每个整数就是一台电脑。于是原来的问题转变成：一开始（即我们还没读取任一对整数），所有电脑都在各自的网络里（其实就是没有任何网络，每个电脑都在一个只有它自己的网络里面）。我们随意挑选两台电脑（也就是开始读入整数对），每当挑选两台电脑，我想问，根据现在已知的网络（已有的输入），这两台电脑是不是处在同个网络里面（是否连通？是否处于同一个等价类）。如果是，我们不做任何处理，继续挑选另外两台电脑（即读取下一个整数对）。如果他们不在同个网络里面，我们要在这两台电脑间连上一条网线（即将他们标记为同个等价类），然后输出这两台电脑的编号（即输出这一对整数），然后我们继续挑选其他电脑（读取下一个整数对）。在这个例子里面，自反性指任何一台电脑都和自己处于同个网络里面；对称性指如果p号电脑和q号电脑相连，那么q号电脑也和p号电脑相连；传递性质如果电脑p、q相连，q、r也相连，那么p、r相连，即p、q、r处于同个网络里面。
人的关系
现在我们拿到一份人员名单，我们给名单上的人都标上号（从0到N-1，共N个人）。那么现在，每个整数代表了一个人。在这个名单上面，有一些人他们之间可能存在亲戚关系，有一些人之间可能没有任何关系。于是现在的问题转变成：一开始（我们还没读取任何的整数对），我们认为这里所有的人之间没有任何关系。然后我们随意挑选两人（也就是开始读入整数对），每当挑选了两个人，我想问，根据已有的亲戚关系（已有的输入），他们两人是不是亲戚呢（这两个整数是不是互相连通？是否属于同个等价类？）如果是，我们什么都不去做。如果不是，我想标记他们两个间是亲戚关系（标记他们为一个等价类），同时写出这两人的编号（即输出这一对整数），然后我们继续挑选其他的人。在这个例子里面，自反性指每个人和自己都是亲戚关系（这个说法有点奇怪，暂时找不到其他的说法）；对称性指如果a是d的亲戚，那么d是a的亲戚；传递性指：省略..亲戚关系的传递性就不用我来说明了。
电路板
假设我们有一块电路板，电路板上有若干个金属的点，现在我们给他们编上号（从0到N-1，一共N个）。那么现在，每个整数代表了电路板的一个点。于是原来的问题转变成：一开始（即我们还没读取任一对整数），电路板上各点之间均不通电。现在我们任意挑选两点（即开始读取整数对），每当选中了两个点，我想问，根据已有的连线，这两个点之间是否通电（专业一点叫做短路，对应问题就是这两个整数对是否连通，是否属于同一个等价类？）。如果他们原来已经是连通的，就不管他，我们继续挑选金属点（读取下一对整数）。如果他们原来没有通电（不在同一个等价类），我要在他们两之间连一条线（标记两个整数为等价类），然后输出这两个金属点编号（即输出这一对整数）。在这个例子里面，自反性指每个金属点和自己是通电的，对称性指如果电量能从p号金属流向q号金属，那么电量也可以从q号金属传到p号金属。传递性指如果p、q两个金属点相通电，q、r两个金属点相通电，那么p、r两点之间也通电的（如果你曾经被电过，我相信你一定理解~~）。
从生活中概括问题
通过以上几个例子，应该能够清晰地解释了动态连通性问题到底是什么，要干什么。连通、等价、等价类，这些都是什么意思。类比生活需要我们抛开严谨的定义，用一些不太严谨但通俗的例子来解释问题。我们不能直接拿着这些例子解题，但是通过这些例子，我们知道我们面对什么问题，我们要干什么事情。现在我们从生活中重新回来，概括问题：
我们有N个整数，并且规定这些整数之间可能会有某种关系。初始化时，我们认为他们之间暂时没有任何关系。现在我们成对读取这些整数，每读一对，都要判断，根据已知的关系网，新读取的一对整数之间是否存在关系。如果存在，忽略他们，继续读取下一对整数，否则的话，标记并且记录他们之间存在关系，同时输出它们的编号。
在电脑的例子当中，连通就是两台电脑之间（直接或者间接地）连着网线，一个等价类代表了一个计算机网络。在人的关系例子里，连通就是两个人是亲戚，一个等价类代表了一大堆的（又或者是一小堆的，甚至仅仅是一个人）亲戚关系。在电路板的例子里，连通是指两个金属点之间相通电，一个等价类代表了一堆被用导线连接的金属点。
我刻意将书本例子展开来讲，可能对于某些人说有点太啰嗦了，但是就我自己学习这个问题那个时候，我就觉得问题本身不好理解，关键就是问题有些抽象，不知道问题到底要干些什么。我相信还是有部分的人会感觉到这个问题不好理解，所以我还是详细地叙述书本里的例子。当你看完这几个例子后，你是不是更加能够理解问题，甚至，你已经对问题求解有了一定的想法呢。
数学抽象
从数学的角度概括问题
理解问题的过程要将问题变得详细，方便理解。而解决问题的过程，则是需要将问题变简单，变得更加容易处理。数学抽象可以精简问题，所以让我们从数学的角度来概括问题。从数学的角度能够看到问题的数学本质——如同书里所提到的，该问题的数学本质是集合与元素。根据集合与元素的关系，我们从数学的角度重新概括问题：
我们有N个元素，同时对应的有N个集合（注意这是初始化的状态，每个元素都默认在一个只有他自己的集合里面）。一旦读取一对元素，我们要问，根据已有的输入，这对元素原本是否属于同个集合里面？如果是，忽略他们，读取下一对元素。如果不是，我们将这两个集合合并，将两个集合变成为一个集合，然后将这两个元素打印出来。接着读取下一对元素。
注意一下
1>书本提到需要注意的一点是，当我们读取元素时，只要关心他们原来是否属于同个集合，并不关心（至少在这个问题里并不关心）从某元素如何走到另外一个元素，也就是说，我只关心两台电脑是否连接，而不关心两台电脑之间经过哪些网线。我只关心两个人是不是亲戚，而不关心某甲是否是某乙的二舅姥爷的嫂子的表妹。同样我也只关心两个金属点之间是不是相通电，而不关心这期间的电路有多复杂。我们所忽略的因素，使得我们能够用数学里的集合来概括问题。如果我们没有忽略这个因素，我们就不能够通过这么精简的集合来概括问题，可能需要添加其他什么标记或者元素，才能概括这个问题。
2>我们现在所讨论的数学集合，是没有删除或者切割操作的集合，这个和某些面向对象的集合非常不同，我们所讨论的问题里面没有"remove"这样子的操作存在，一旦两个元素被放进了一个集合里面，他们永远都在一个集合里面，就算合并两个集合，原来在一起的元素还在一起。
我们具体要做什么
从数学的角度概括问题，就是为了能够精简问题，从而得到问题的解。既然我们已经对问题进行了概括，现在需要根据我们所概括的情况，得到解决该问题需要做的事：
1>初始化时，我们会有N个元素，同时对应N个集合，N个元素直接用0到N-1个整数来标识，那么如何才能标识N个集合，同时还要将N个元素与它们对应的集合对应起来？
2>当我们读取了某一对元素时，需要判断他们两个是否处于同个集合（这个就是问题1，如果解决了问题1，这个就不是问题了），然后如果他们原来不是同个集合，我们如何将他们各自所属的集合并在一起（其实这个是问题1引申，如果你能标识N个集合，在需要合并的时候，只要修改集合标志就可以了）。
问题小结：最后我们总结一下，我们啰嗦了那么久，解决问题就是做到：
1>对于某个给定元素（某个整数），能够查到它所在的集合。
2>当读取到两个不同集合里的元素，可以将两个集合合并。
解决动态连通性问题，核心就是解决这两句话。
从数学到问题的解
从数学到API
我们已经高度概括我们要做什么，为了将我们要做的事情再具体化，我们需要根据我们做的概括，写出API，好让我们可以继续解决问题。既然我们输入的是整数，那么就可以直接用整数标志各个元素，同时，也很自然而然地可以用整数表示各个集合，所以抽象出来的API如下：
int find(int p);//对于某个给定元素，能够查到他所在的集合，函数输入的是元素，返回的是该元素所在的集合（的标识）。
void union(int p, int q);//当读取到两个不同集合里的元素，可以将两个集合合并，函数的输入是两个集合里的元素，函数会将两个集合合并。
boolean connected(int p, int q);//判断两个元素是否属于同个集合，很显然的，这个方法只要调用"find()"方法并作一些处理即可。从API到数据结构
数据结构的性质将直接影响到算法的效率，因此数据结构和算法的设计是紧密相关的。——《算法》（第四版中文版）。
根据书本的轨迹，我们已经做完了这些事：提出问题、理解问题（类比生活理解问题）、概括问题（从生活中概括问题，再从数学层面概括问题）、得出API（从数学的精简抽象当中，概括出了API）。能够得到API已经是非常具体的一件事。现在我们再具体些：得到实现API的数据结构。不论你是用哪一个数据结构，根据我们之前说得到的结论，你的数据结构需要能够做到以下事情：
1>对于某个给定元素，能获取到它所在的集合。
2>能够合并不同集合里的元素。
现在我们来看一下，书本里的算法如何做到这两件事。
quick-find算法
算法思想
"quick-find"算法使用数组解决这个问题，他用数组下标表示每个元素，数组每个位置所存的值，就是这个元素所在集合。
什么意思呢，这里我们展开来讲，我们通过前面电脑那个例子理解。假设我们在电脑的左右两边分别贴上一张标签，左边那张标签表示这台电脑本身的编号，右边那个标签表示这个电脑所处的网络的编号。初始化时，每个电脑左边那个标签的值等于右边标签的值（因为初始化的时候，直接用电脑的编号代表电脑所在网络）。我们随意挑选两台电脑，只要查看他们两个的右标签是否相等，就能知道他们是否处于同个网络里面。假设我们现在挑选左标签为p、q两台电脑，p电脑的右标签为m，q电脑的右标签为n，此时我们需要做的，就是找到这间房里所有右标签的值为n的电脑，然后将它们右标签都改成m。然后继续挑选新的电脑。这里，左标签就表示数组下标，同时也是元素自身编号，右标签就表示数组每个位置具体的值，同时也是元素所处集合。
现在我们知道这个算法如何解决我们所提出的两个事情：
1>对于一个给定元素，我们只要获取数组里面该下标所对应的值，就是这个元素所在集合。
2>如果要将x、y两个集合合并，只要遍历整个数组，将数组里所有存着x的数改成y就可以了（反之亦可）。
"find()"方法与"union()"方法耗时
在我们使用数学的方法严谨地计算算法的效率之前，我们通过电脑网络这个例子想象一下，如果让你判断两台电脑是否处于同个网络，很容易吧，你用眼睛看下就好，但是如果让你合并两个计算机的网络，你每次都需要跑遍整间房间，那么现在"quick-find"算法的特性也就出来了：
对于"int find()"方法，它很高效，但是对于"union()"方法，每次都要遍历整个数组，随着数组元素越来越多，越来越慢。
现在我们严谨地来计算一下（需要说明的一点是，我们使用“访问数组的次数”代表“时间复杂度”），首先是"find()"方法，如下：
//这个方法不用计算时间复杂度了，他就是1
public int find(int p){
return id[p];
}
现在来看"union()"方法，如下：
public void union(int p, int q){
//分别获取元素p和q所在连通分量标识
int pID = find(p);//1号语句，这条语句需要访问1次数组
int qID = find(q);//2号语句，这条语句需要访问1次数组
//如果他们处在同个连通分量里面，直接返回
if(pID == qID){
return;
}
//遍历所有的元素，当遇到和p处于同个连通分量的元素，将他们的连通分量改成与q相同，就是合并连通分量
for(int i = 0; i < id.length; i++){
if(id[i] == pID){//3号语句，这条语句需要访问n次数组
id[i] = qID;//4号语句，这条语句最少执行1次，最多(n-1)次
}
}
count--;//标记连通分量少了一个
}
在最好的情况下是：1+1+n+1 = n+3。
在最坏的情况下是：1+1+n+(n-1) = 2n+1。
注意这是"union()"方法的时间复杂度，不是整个问题耗时。
总耗时
分析完了"union()"方法之后，我们可以很快得到"quick-find"算法解决问题的复杂度。对于算法耗时分析，我们总要分析最坏那个情况。那么"quick-find"算法最坏的情况是怎么来的？根据我们已知道的，我们可以这样推出最坏情况：
"union()"方法调用次数越多，访问数组次数就会越多，越是耗时-->最终剩下的连通分量个数越少，则"union()"方法被调用的次数越多（因为"union()"方法每次都会减少一个连通分量）-->如果最后只剩下了一个连通分量，则"union()"方法被调用的次数达到最大，则此时的输入耗时达到最大。所以，假设每次输入都会减少一个连通分量，那么对于n个元素，在经历了(n-1)次输入之后（也就是在调用了(n-1)次"union()"方法之后），需要访问数组的次数最少是：(n+3)(n-1)→O(n2)
这个分析所得到的，是指如果最后我们就只得到一个连通分量，那么不论你以什么顺序输入，你最少要访问数组(n+3)(n-1)次。最后我们得出的结论是，"quick-find"算法对于最终只能得到少数连通分量的输入，所需要的处理时间是平方的级别。
quick-union算法
算法思想
"quick-unioin"算法与"quick-find"算法都是使用数组解决问题，也用数组下标直接表示元素，但是数组每个位置所存储的元素含义不同。现在我们展开来讲：
初始化时，我们一共有n个结点，对应n棵树，每个节点都是它自己所在的那棵树的根节点。我们开始读取数据对，每读取到两个元素，我想问，它们两个是否处于同一棵树？如果是，那忽略它，如果不是，我将这两棵树合并。合并的具体做法是，将A树的根，直接挂到B树的根下，原来A树的根节点，成为B树第二层的节点。在这个算法里面，数组下标仍然表示每个节点，某个下标里面所存的值，是该节点在树里面的父节点。每一棵树代表一个集合，每棵树的根节点标识着这个集合。很显然地，对于每一个给定的元素，我们总能找到它所在那棵树的根节点。
现在我们知道这个算法如何解决我们概括出的两个问题：
1>对于某个给定元素，我们获取到根节点，就获取到他所在的集合。
2>如果要将p、q两个元素所在的结合合并，只要将p所在的树的根，挂到q所在的那棵树的根下（反之亦可）。
"find()"方法与"union()"方法耗时
在使用数学方法来计算效率之前，我们仍然想象一下，对于"find()"方法，从一棵树任一节点向上追索，直到找到其根节点，很显然地效率一定小于（等于）"quick-find"算法。对于只有一个节点的树，"find()"方法效率和"quick-find"算法一样。但是随着树越长越高，"find()"方法耗时可能将会越来越长（只是可能，因为这取决于输入），最终得到n阶耗时。而对于"union()"方法，显然每次执行这个方法，最多只要在两个元素的树里面做遍历，而不需要扫描所有的树（不用遍历整个数组）。单从这个方面来讲，它的效率一定高于（等于）"quick-find"算法里的"union()"方法，但是具体能快多少，它有很大的浮动性，因为输入顺序不同，将会导致我们拼接出来的每棵树深度不同，甚至树的数量也不一样。
现在我们严谨地来计算一下，先看"find()"方法：
private int find(int p){
while(p!=id[p]){//1号语句，最好情况下仅执行一次，最坏情况下要执行(n+1)次
p = id[p];//2号语句，最好情况下不执行，最坏情况下会执行n次
}
return p;
}
对于深度为零的节点，"find()"方法的1号语句就执行一次，2号语句不用执行，此时算法总共需要访问数组1次。而当节点的深度为n（注意了这里的n是节点深度，不是元素或节点的个数），"find()"方法需要对数组做(2n+1)次的访问（1号语句2号语句各自执行一次，就能沿着“树枝“往上“爬”一层，对于深度n，需要“爬”n次，一共访问2n次数组，然后最后还要执行一次判断，此时该判断一定会成立，因为已经“爬”到了，所以最终就会访问数组2n+1次）。
public void union(int p, int q){
//分别找到两棵树根节点
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot){
return;
}
//将一棵树挂到另外一棵树下
id[pRoot] = qRoot;
count--;//连通分量个数减一
}
显而易见，该方法就是在两次"find()"方法之后，再加一次数组访问（如果给定两个元素原来就在一棵树下，那就只有两次"find()"方法调用，不用再加一次数组访问）。你在这里千万不要想当然的觉得访问次数==2(2n+1)+1，两个元素所在的树不一定是同一棵树，就算他是同一棵树，两个元素也不一定处在同个深度里面，"union()"访问数组的次数受具体元素影响。由于我们已经得出"find()"方法耗时，而且"union()"耗时主要还取决于"find()"方法，那么对于"union()"耗时，我们能有大概的结果了，但是没有必要精确计算。同时，这也很难精确计算。
总耗时
从上面的分析得到，整个问题的总效率，基本就由"find()"方法决定，所以我们只要研究在不同的情况下面，"find()"方法的耗时即可。
如同分析"quick-find"方法，我们也来推导一下最坏情况，我们知道：
"union()"方法耗时受"find()"方法影响-->"find()"方法耗时受所输入元素在树里的深度影响，而且每棵树里最“底层”那片叶子就是树里深度最大那个节点，同时该深度就等于树的深度-->树的深度受输入的顺序影响，同时也受最终连通分量个数影响。但是我们可以想象，如果最终只得到一棵树，而且这棵树每一个节点，最多只有一个孩子时，此时树的深度达到最大。现在我们可以得到最坏情况下的输入。假设我们现在输入p、q两个整数，并且每次都将整数p所在树，挂到q所在的树下。
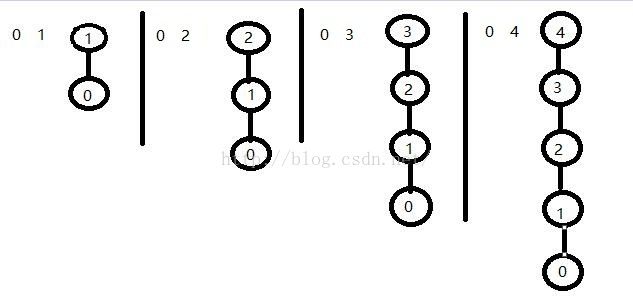
现在讨论最坏情况，一图胜千言。笔者画图技术不好，不要见怪。在最坏的情况下，我们读到如下图所示一棵树（每列左边数字表示的是每次输入，右边表示输入之后这棵树会长成什么样子）。从左到右看这幅图，这个输入将会逐渐得到一棵深度很大的树。
最坏情况是这样的：
每次输入的整数对都是(0,i)其中i=1,2,3....(n-1)，然后最后还只剩下一个连通分量。就能得到图中所示这个情况。在这个情况下面，每次调用"union()"方法，它会发生(2n+1)+(2m+1)+1次的数组访问（其中n为上图所示0元素所在的深度，m是整数对(0,i)里面i元素所在的深度，很明显地m == 0，最后的1是指合并两棵树的操作，他会访问一次数组），所以最终它会发生(2n+1)+1+1 = (2n+3)次的数组的访问。由于i是有规律变化的，我们还能将这个式子再具体一点：对于整数对(0,i)，"union()"操作将会访问数组2i+3次，节点0的元素深度为i，节点i的深度为零。所以处理n对整数所调用的"union()"方法，对数组做的访问次数为(2i+1)（其中i从1到n变化），即2(1+2+....+n)+n~O(n2)（由于存在平方项，所以省略n）。在最坏的输入结果同时最坏输入顺序之下，访问数组的次数为平方阶的。
根据我们刚才说得，如果最后只剩下了一个连通分量，可以得到最坏情况，但是我们也提到过，算法耗时还受输入顺序影响。现在我们来看一下，在最后只得到一个连通分量的情况下，算法耗时最少情况，一图胜千言：
同样，每列上边数字表示每次输入，每列下边表示输入之后这棵树的样子。从左到右看这幅图，将会得到一棵深度超小的树（深度==1），最好情况是这样的：
每次输入的整数对都是(i,0)其中i = 1,2,3...(n-1)，然后最后剩下一个连通分量。就能得到如图所示情况。在这个情况之下，每次调用"union()"方法，它会发生(2n+1)+(2m+1)+1次的数组访问（其中n为0元素所在的深度，m为i元素所在的深度，由图可知n == m == 0），所以每次调用了"union()"方法，访问数组的次数为3（超级快）。那么按照这个输入，对于编号为0~(n-1)的整数，输入(n-1)对整数之后，将会调用(n-1)次"union()"方法，最终得到1个连通分量，访问数组的次数为3(n-1)~O(n)，此为线性的复杂度。
对于以上分析我们得到，如果最后剩下一个连通分量，在最好的情况之下，"quick-union"算法耗时仅仅达到线性级别，大大优于"quick-find"，然而如果在最坏的输入顺序之下，"quick-union"算法耗时依旧达到平方级别，相比较于"quick-find"算法，提高的并不明显。
加权quick-union算法
回顾原始"quick-union"算法，根据之前做的分析，我们可以很容易地看出，"quick-union"算法效率主要受到树的高度影响，尤其是在最坏输入的情况下。算法效率低实际上就是由于树太高了。同时回头看一看"quick-union"算法里的最坏情况，可以发现，如果我们经常将较高的树挂到较矮的树下，就会导致整个算法效率低下。按照这样子的想法，就得到了加权的"quick-union"算法：每次合并两棵树时不再是随机的，总是要将较小的树挂到较大的树下面。这样就能避免得到一棵长得好像“单链表”那样的树。
算法思想
加权"quick-union"算法，是在普通"quick-union"算法的基础上进行改进，基本思想和原来的是一样的，只是加了一个数组，用来记录每棵树的节点个数。我们知道在原来的"quick-union"算法里面，每个集合（每棵树）由根节点来做标志。所以在加权"quick-union"算法里面，新添加的数组的含义是：这个数组的下标，就是树的根节点，某个下标对应的值，就是这棵树的节点个数。比如某棵树根节点为元素m，如果size[m]的值为n，那么表示“以m元素为根节点的那棵树，一共有n个节点”。其实这个数组的作用，就是输入根节点，获取根节点所在树节点个数。
这里帖出了完整的加权"quick-union()"算法，虽然重点仍然是在"find()"方法以及"union()"方法里面，但是由于多了一个数组，同时还要做一些初始化，为了不显得太突兀，还是贴出完整代码。
public class WeightedQuickUnionUF{
private int[] id;
private int[] sz;//这个数组用来记录每棵树的节点个数
private int count;
public WeightedQuickUnionUF(int N){
count = N;
id = new int[N];
for(int i = 0; i< N; i++){
sz[i] = 1;//初始化时，每棵树的节点个数都是1个
}
}
public int count(){
return count;
}
public boolean connected(int p, int q){
return find(p) == find(q);
}
public int find(int p, int q){
while( p != id[p]){
p = id[p];
}
return p;
}
public void union(int p, int q){
int i = find(p);
int j = find(q);
if(i == j){
return;
}
if(i算法效率
由于我们已经详细分析过了原始"quick-union"算法效率，就不需要从头分析加权后的算法效率。同时对于加权的"quick-union"算法，研究的核心应该是在各种的输入下面，树的高度如何变化。我们依旧来推导下最坏情况：
加权"quick-union"算法效率比原始的提高，是由于加了数组来记录树的节点个数，本质上是每次合并那时多了一句判断代码-->如果这句判断代码没有意义，那么加权"quick-union"算法做的优化效果变差-->判断代码每次都将小树挂到大树上面，如果两棵树每次都是一样大,那么判断代码没有意义，此时加权算法达到最坏情况。
好了现在我们得到最坏情况下的输入：
如果总共有偶数个元素，我们的输入导致了，每次都是两两合并，然后再到每次都是四四合并，然后再到八八合并。这样子的输入情况就会使得加权"quick-union"算法“表现”最差。因为这个输入之下加权"quick-union"算法用来优化所加入的判断语句，所起作用已经很不明显。如图，这图是从书本里抄来的。
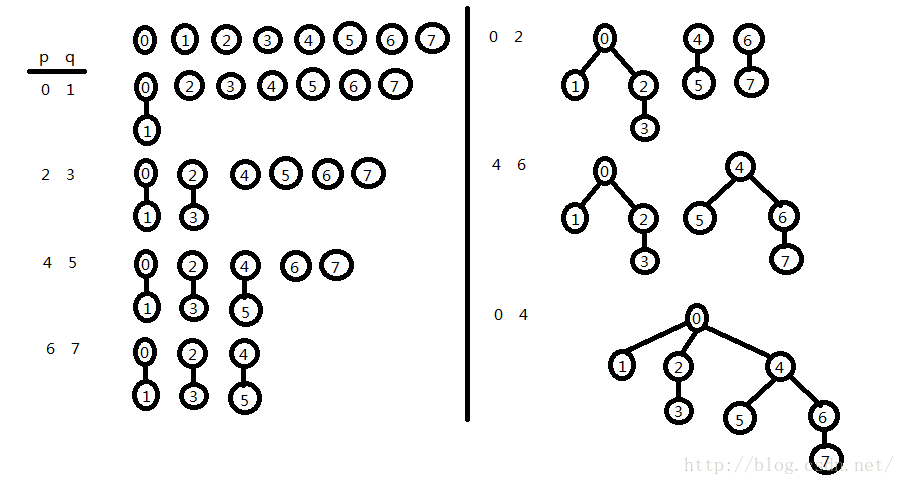
至此，我们看到了加权"quick-union"算法最坏情况下的效果，很显然地，比起原始的"quick-union"最坏情况下的树的高度，明显的优化了很多，而这仅仅是添加了一个数组以及一些判断语句。
这篇笔记写到这里，已经基本完成了算法问题的理解、分析、设计算法以及算法分析，对于加权"quick-union"算法总体效率分析，以及后面路径压缩算法，书本已经分析的很详细，笔者也没有什么新发现，也就觉得没有必要又将答案在抄一遍。这篇笔记写到这里差不多了。
总结
本文所写是笔者对《算法》动态连通性问题的梳理。我们经过理解问题、设计具体算法以及编写代码解决问题、算法分析三个阶段深入理解动态连通性问题。
>在理解问题的阶段，我们通过提出问题-->类比生活，理解问题-->从生活中概括问题-->通过数学抽象高度概括问题这一系列步骤理解问题实质。
>在设计算法及编写代码阶段，我们通过从数学抽象推导API-->由API选择具体数据结构-->根据数据结构编写代码，并且获得一个初步的解。
>在算法的分析阶段，针对每一类算法（其实一共也就两类），都描述了算法思想，单独分析"find()"方法以及"union()"方法耗时，由算法的特性推导最坏情况下的输入，并且计算最坏情况下算法的耗时。进而对比不同算法优劣。
乍看之下我们似乎做了很多事情（三个阶段并且每个阶段还有一系列的步骤），其实可以简要概括一下，对于以后会遇到的算法问题，我们需要：
>详细理解问题并且通过数学抽象精确定义问题。
>通过数学抽象写出解决问题所需的API，根据API来选择数据结构并且设计算法。
>针对数据结构特性以及算法特性分析算法，尤其需要根据算法特性分析最坏输入时的算法耗时，同时还要在不断迭代中改进算法。