高等数学——积分中值定理
本文始发于个人公众号:TechFlow,原创不易,求个关注
今天是高等数学专题的第12篇,我们继续来看定积分。
之前在讲微分求导内容的时候,介绍过一系列微分中值定理的推导。既然有微分中值定理,那么自然也有积分中值定理,我们下面就来看看积分中值定理的定义。
极值定理
极值定理也叫最大最小值定理,它的含义非常直观:如果函数f(x)在区间[a,b]上连续的函数,必然存在最大值和最小值,并且取到最大值和最小值至少一次。
这是一个非常有名的定理,定理的内容很直观,也不难理解。但是证明它不太容易,是由区间套定理与B-M定理等多个定理推导得到的,这段证明过程比较复杂,由于篇幅和水平的限制,本文当中只能跳过这部分,感兴趣的同学可以自行了解。
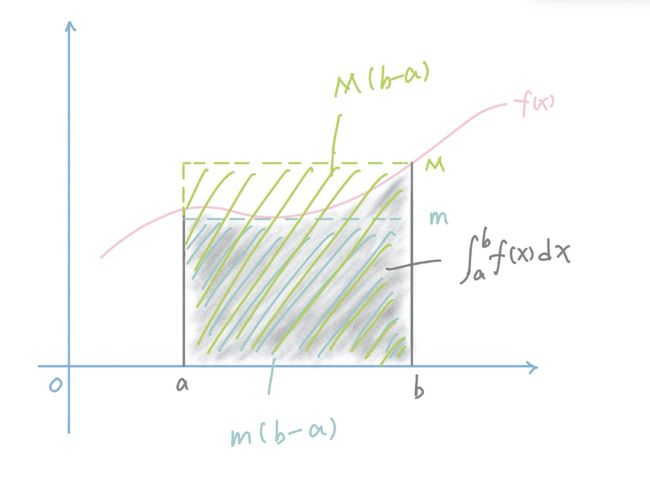
我们假设m和M分别是区间[a, b]上函数f(x)的最小值和最大值,那么根据极值定理,可以得到以下式子成立:
m ( b − a ) ≤ ∫ a b f ( x ) d x ≤ M ( b − a ) m(b-a) \leq \int_a^bf(x)dx \leq M(b-a) m(b−a)≤∫abf(x)dx≤M(b−a)
这个式子光看可能会觉得有些复杂,但是我们把图画出来之后非常简单:
上图当中灰色阴影部分就是定积分的结果,蓝色的矩形面积是m(b-a),大的矩形面积是M(b-a)。
通过几何面积的关系我们可以很容易证明结论。
数学证明也很简单,由于m和M分别是最小值和最大值,所以我们可以得到 m ≤ f ( x ) ≤ M m \leq f(x) \leq M m≤f(x)≤M。我们把常数也看成是函数,进行积分,于是可以得到:
∫ a b m d x ≤ ∫ a b f ( x ) d x ≤ ∫ a b M d x \int_a^bm dx \leq \int_a^b f(x)dx \leq \int_a^bMdx ∫abmdx≤∫abf(x)dx≤∫abMdx
两边积分的结果就是矩形面积,于是我们就得到了证明。
积分中值定理
极值定理非常简单,但是是很多定理的基础,比如我们的积分中值定理就和它密切相关。
我们对上面的式子做一个简单的变形,由于b-a是常数并且大于0,所以我们在 m ( b − a ) ≤ ∫ a b f ( x ) d x ≤ M ( b − a ) m(b-a) \leq \int_a^bf(x)dx \leq M(b-a) m(b−a)≤∫abf(x)dx≤M(b−a)这个不等式两边同时除以b-a,可以得到:
m ≤ 1 b − a ∫ a b f ( x ) d x ≤ M m \leq \frac{1}{b-a}\int_a^b f(x)dx \leq M m≤b−a1∫abf(x)dx≤M
我们把 1 b − a ∫ a b f ( x ) d x \frac{1}{b-a}\int_a^b f(x)dx b−a1∫abf(x)dx这个式子看成一个整体,它的值位于函数在区间的最大值和最小值之间。根据连续函数的介值定理,我们一定可以在[a, b]上找到一点 ξ \xi ξ,使得f(x)在 ξ \xi ξ这点的取值与这个数值相等,也就是说:
1 b − a ∫ a b f ( x ) d x = f ( ξ ) , ( a ≤ ξ ≤ b ) \frac{1}{b-a}\int_a^b f(x)dx = f(\xi),\quad (a \leq \xi \leq b) b−a1∫abf(x)dx=f(ξ),(a≤ξ≤b)
上面这个式子就是积分中值定理了,这里有两点要注意,我们先来说简单的一点,就是我们用到了连续函数介值定理。所以限定了这必须是一个连续函数,否则的话,可能刚好函数在 ξ \xi ξ点处没有定义。这个也是定理成立的先决条件。
第二点是简单介绍一下连续函数的介值定理,它的含义是说对于一个在区间[a, b]上连续的函数,对于任一在其最大值和最小值之间的常数,我们必然可以在区间[a, b]上找到一点,使得该点的函数值等于这个常数。
搞明白这些细节之后,我们再来看刚才的式子:
f ( ξ ) = 1 b − a ∫ a b f ( x ) d x , ( a ≤ ξ ≤ b ) f(\xi) = \frac{1}{b-a}\int_a^b f(x)dx ,\quad (a \leq \xi \leq b) f(ξ)=b−a1∫abf(x)dx,(a≤ξ≤b)
我们再把常数乘回来:
( b − a ) f ( ξ ) = ∫ a b f ( x ) d x , ( a ≤ ξ ≤ b ) (b-a) f(\xi) =\int_a^b f(x)dx ,\quad (a \leq \xi \leq b) (b−a)f(ξ)=∫abf(x)dx,(a≤ξ≤b)
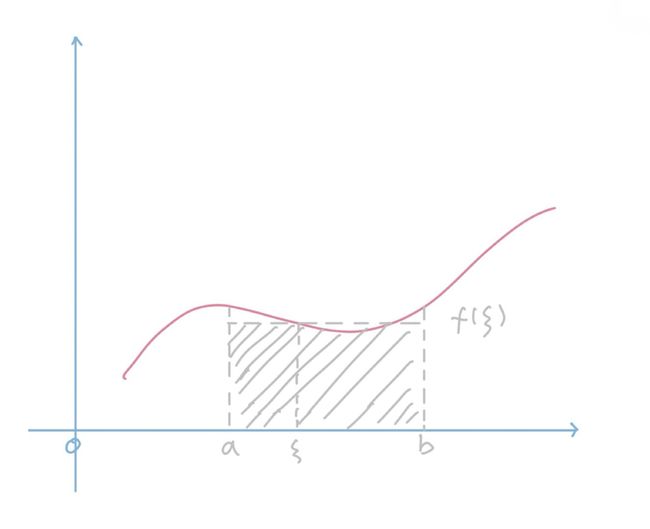
右边的积分算的是什么,算的是函数围成的曲形的面积,但是现在我们转化成了一个函数值乘上了宽,所以我们可以把它看成是矩形的高,我们来看下下面这张图。
也就是说以 f ( ξ ) f(\xi) f(ξ)为高的矩形面积和函数围成的曲形面积相等,所以它既是矩形的高,也真的是函数在[a, b]上的平均值。
总结
中值定理是微积分领域当中最重要的定理,几乎没有之一,也是整个微积分搭建起来的脉络。我们熟悉中值定理的推导过程,对于我们对加深对于微积分的理解非常有帮助。更重要的一点是,相对来说,这两个定理的推导过程都不是很难,而且还蛮有意思的,所以推荐大家都亲自上手试一试。
今天的文章就是这些,如果觉得有所收获,请顺手点个关注或者转发吧,你们的举手之劳对我来说很重要。