S型曲线加减速
1、 S型曲线
1.1 简介
Sigmoid函数是一个在生物学中常见的S型函数,也称为S型生长曲线。Sigmoid函数也叫Logistic函数,取值范围为(0,1),它可以将一个实数映射到(0,1)的区间,可以用来做二分类。该S型函数有以下优缺点:优点是平滑,而缺点则是计算量大。
Sigmoid函数由下列公式定义:
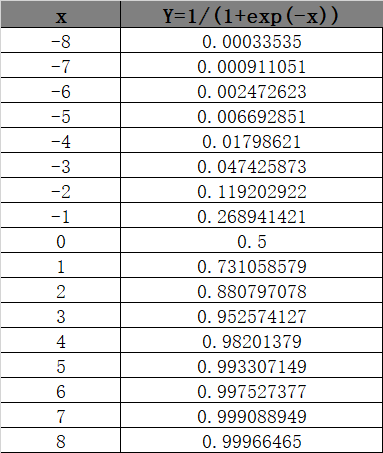
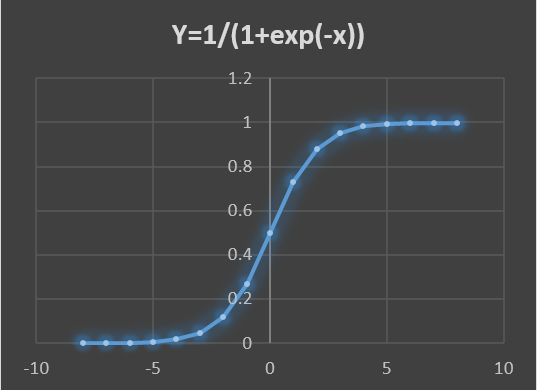
Sigmoid函数在[-8,8]的计算数值以及图形如下:
由以上数据与图形可见,S型曲线就是指图形中变化阶段的曲线呈现一个英文字母'S'型,该曲线无限趋向于0和1,即取值范围为(0,1)。
1.2 曲线延伸
| 函数延伸 |
说明 |
取值范围 |
| Y = A + 1 / ( 1 + exp( -x ) ) |
A分量在Y方向进行平移 |
( A , A+1 ) |
| Y = B / ( 1 + exp( -x ) ) |
B分量在Y方向进行拉伸 |
( 0 , B ) |
| Y = 1 / ( 1 + exp( -ax ) ) |
a分量在x方向进行平移 |
( 0 , 1 ) |
| Y = 1 / ( 1 + exp( -x+b ) ) |
b分量在x方向进行拉伸 |
( 0 , 1 ) |
| Y = A + B / ( 1 + exp( -ax + b ) ) |
同上 |
( A , A+B ) |
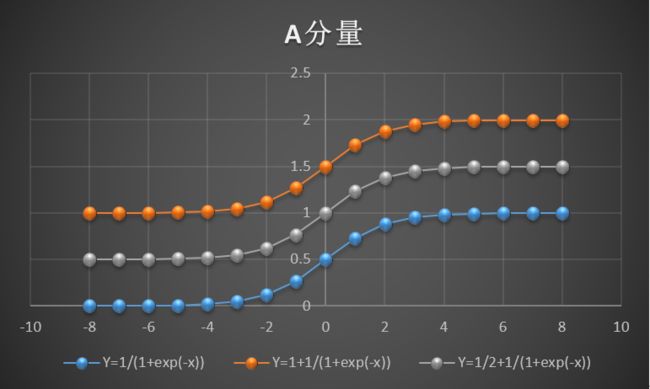
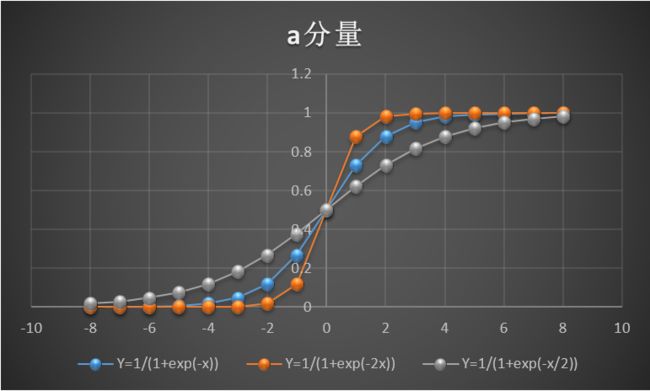
为了更直观地观察A、B、a、b分量对函数的影响,我整理 了一下对应的曲线图,如下所示:
由图可见,A、B分量影响的是曲线的取值范围,而a、b分量影响的则是曲线的平滑程度。
2、应用场景 – 电机加减速控制
2.1 简介
电机加减速,顾名思义,即电机以加速方式启动,速度达到预设目标速度后保持一段时间匀速转动,随后又开始以减速方式转动直至电机以一个较低的速度停止转动。
一方面,电机加减速可以避免电机急开急停,进而可能对电机造成一定损坏;另一方面,也可以防止电机在高驱动速度不能起步的情况,即高驱动速度会出现空转、丢步现象。因而,在电机需要达到一个较高的速度时,通常需要采用慢速加速驱动的方法,简而言之,就是需要有一个加速过程。
例如:步进电机驱动负载可以按目标速度起动,若目标速度超过自身起动脉冲频率时,则该情况下不能起动。因而,只有当起动频率比电机起动脉冲频率低时才能正常起动,采取加速的方式使速度线性地增加到目标速度,这种方法则称为慢速加速驱动。
2.2 T型与S型
目前,在电机加减速控制上,普遍的加减速方法主要有T型加减速和S型加减速,实现方法则有公式法或查表法。
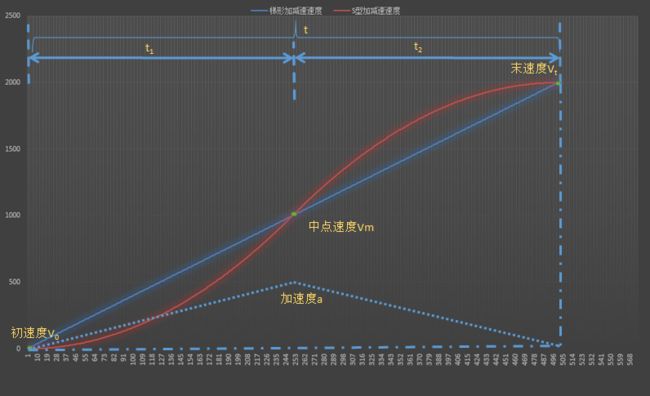
S型加减速相对于T型加减速更加平稳,对电机和传动系统的冲击更小,即S型加减速的优点是启动和停止都很平滑,不会有很大的冲击,但是也并非不存在缺点,缺点就是启动和停止的时间比较长。
2.3 电机加减速控制
如要将S型曲线应用到电机的加减速控制上,需要将方程在X、Y坐标系进行平移,同时对曲线进行拉升变化:即 Y = A + B / ( 1 + exp( -ax + b ) ) ,则根据该曲线方程的相关特征可知,A、B分量可用于控制电机速度(频率)的取值范围,而a、b分量可用于控制速度(频率)变化率。最终根据实际的需要,在加减速过程中采用以下的曲线方程为:
Fcurrent = Fstart + (Fend-Fstart)/(1+exp( -Flexible(i - Num )/ Num) )
注:
| Fcurrent |
当前频率值 |
| Fstart |
起始频率值 |
| Fend |
目标频率值 |
| Flexible |
S型曲线拉伸变化。Flexible代表S曲线的平滑程度,Flexible越大说明加速度越大,即曲线越陡,Flexible越小说明曲线越平滑,理想的S曲线Flexible取值为4 ~ 6。 |
| Num |
Num一般取值为 Length/2 大小,这样可以使得S曲线对称,Length为加减速点的总个数 |
| i |
循环计算过程中的索引,从0开始,到 Length结束 |
以上公式既可当作加速曲线,也可当作减速曲线。因此,一般情况下,我们只需要计算加速曲线,在减速时作反向操作即可。电机从10kHz加速到100kHz的加速曲线以及从100kHz减速到10kHz的减速曲线示例如下所示:
2.4 示例代码
在电机加减速控制上,电机频率越大,电机速度越快。因而,可以通过公式法求出每个加减速点的频率值,进而通过电机频率求出具体的脉冲周期,最后在间隔相同的时间内改变脉冲相关参数(分频、周期、占空比)即可达到加减速的效果。一般情况下,如步进电机、伺服电机等,分频与占空比通常固定数值即可,这样在加减速过程仅需改变输出周期值即可。同时,不同频率脉冲输出时也需要注意脉冲的连续性(即我们需要在当前脉冲完全输出之后才能改变电机频率),否则电机加减速过程就会出现丢步现象,在脉冲数严格要求的情况下造成累积误差。
1 /** 2 * @brief: 【公式法】S型加减速曲线计算,公式:Y=Fstart+(Fend-Fstart)/(1+exp(-flexible*(x-num)/num)) 3 * @param [OUT] Fre[] 输出频率值 4 * [OUT] Period[] 输出周期值 5 * [IN] Len 变速脉冲点 6 * [IN] StartFre 开始频率 7 * [IN] EndFre 结束频率 8 * [IN] Flexible 曲线参数 9 * @return: none 10 * @Date: 2020-08-12 10:32:03 11 */ 12 void Calculate_S_Curve(float Fre[], u32 Period[], float Len, float StartFre, float EndFre, float Flexible) 13 { 14 float melo; 15 16 for(int i = 0; i < Len; i ++) 17 { 18 melo = Flexible * (i-Len/2) / (Len/2); 19 Fre[i] = StartFre + (EndFre - StartFre) / (1 + expf(-melo)); 20 Period[i] = (u32)(TIM_CLK / TIM_FRESCALER / Fre[i]); // TIM_CLK 定时器时钟 TIM_FRESCALER 定时器分频 21 } 22 }