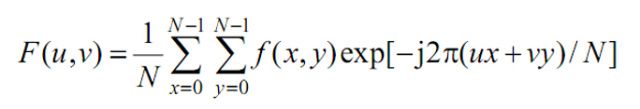编解码中的高频和低频
一、转自 https://blog.csdn.net/weiaipan1314/article/details/51482300
如何从频谱图看一副图像的高频和低频成分
形象一点说:亮度或灰度变化激烈的地方对应高频成分,如边缘;变化不大的地方对于低频成分,如大片色块区画个直方图,大块区域是低频,小块或离散的是高频把图像看成二维函数,变化剧烈的地方就对应高频,反之低频。
举个通俗易懂的例子:
一幅图象,你戴上眼镜,盯紧了一个地方看到的是高频分量
摘掉眼镜,眯起眼睛,模模糊糊看到的就是低频分量。
图像的高低频是对图像各个位置之间强度变化的一种度量方法.
低频分量:主要对整副图像的强度的综合度量.
高频分量:主要是对图像边缘和轮廓的度量.
如果一副图像的各个位置的强度大小相等,则图像只存在低频分量,从图像的频谱图上看,只有一个主峰,且位于频率为零的位置.
如果一副图像的各个位置的强度变化剧烈,则图像不仅存在低频分量,同时也存在多种高频分量,从图像的频谱上看,不仅有一个主峰,同时也存在多个旁峰.
以上的现象可以通过对傅里叶变换的公式分析得出.
以下所说的积分是对x进行的.
exp(-jwx)的数值变化是均匀的,如果对exp(-jwx)进行积分,则积分值为零.如果对exp(-jwx)乘以一个加权函数f(x),则在对f(x)exp(-jwx)进行积分,积分值不一定为零.如果exp(-jwx)的取值为1时,则对f(x)exp(-jwx)积分,既为对f(x)积分,此时f(x)exp(-jwx)最大,既频谱中的主峰.如果f(x) 是常数则, 除w=0处f(x)exp(-jwx)的积分不为零外,在w不为零的其它处,f(x)exp(-jwx)的积分都为零.
二、转自 https://www.zhihu.com/question/29246532?sort=created
图像傅里叶变换的频率怎么理解?
请问图像的傅里叶变换里面,怎么理解高频和低频呢?是u,v大的值对应高频么?傅里叶变换以后得到的幅度谱为什么能反映灰度的变化情况呢?看了很多资料,一直缺乏直观上的理解啊,哪位大神能给讲一下?谢谢
图像不过是个二维数组,方便理解起见,咱们可以考虑一维数组.
下面的例子可能不严谨,但绝对很直观.
比如有如下数组
{1, 10, 1, 10, 1, 10, 1, 10, 1, 10, 1, 10}
和
{1, 2, 3, 4, 5, 4, 3, 2, 1, 2, 3, 4, 5, 4, 3, 2, 1,}
你直观的理解下,哪个数组的"频率"大点?
你可以用纵坐标代表数组值,横坐标代表数组index描点看看,显然是第一个数组的频率高.
所以对于数组来说,数字之间变化剧烈,代表高频,柔和代表低频.
同理,对于图像来说,那就是灰度变化快的是高频,慢的是低频.比如一个物体的边缘,就是高频信号,物体内部,就是低频.
而傅立叶变换无非是告诉你这副图像上XXX频率的信号有多少多少, YYY的频率有多少多少.
那换句话说就是,图像的傅立叶变换可以让你直观的看到这幅图总体上"剧烈"的变化有多少,"柔和"的变化有多少.
一副整体很模糊的图,傅立叶变换后显示的低频分量就很多
一副整体灰度变化很剧烈的图,傅立叶变换后显示的高频分量就很多
同理,如果你在频域上将高频分量去掉,再反变换回去,那图片就会变的模糊.
三、转自 https://www.cnblogs.com/lyj0123/p/10504224.html
3_一幅图像,经过傅里叶变换后,将高频部分删除,再进行反变换,设想一下将会得到什么结果?
一幅图像,经过傅里叶变换后,将高频部分删除,再进行反变换,设想一下将会得到什么结果?
在频谱图上,白色的斑点、噪声和边界等会表现为高频部分,所以通过滤去高频,可以降噪(图像的频谱函数统计特征:图像的大部分能量集中在低频和中频中,高频部分的分量很弱,仅仅体现了图像的某些细节。因此,滤波器滤噪,也就是除去高频部分、能量低的部分)。傅里叶变换将时域转换为频域,对频域图像进行消噪,然后再反变换为时域,就达到了消除噪声的效果。