LeetCode初级算法——【数组专题】
一. 删除排序数组中的重复项
给定一个排序数组,你需要在 原地 删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
在数组中灵活运用指针,不断用元素覆盖当前指针
public int removeDuplicates(int[] nums) {
int length = nums.length;
int i = 0;
for(int j=1;j<length;j++){
if(nums[i]!=nums[j]){
i++;
nums[i] = nums[j];
}
}
return i+1;
}
二. 买卖股票的最佳时机
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)
public int maxProfit(int[] prices) {
int length = prices.length;
//dp[i]表示第i天可以获取的利润
int[] dp = new int[length];
for(int i = 0;i<length-1;i++){
if(prices[i]<prices[i+1]){
dp[i] = prices[i+1] - prices[i];
}
}
int max = 0;
for(int i=0;i<length;i++){
max += dp[i];
}
return max;
}
3. 旋转数组
给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。

public void rotate(int[] nums, int k) {
int length = nums.length;
if(length<=1){
return;
}
//计算实际需要旋转的步长
if(k>length){
k = k % length;
}
int[] arr = new int[length];
for(int i=0;i<length;i++){
arr[i] = nums[i];
}
for(int i=0;i<length;i++){
//求出新数组元素的相对偏移量
int s = i + k;
s = s % length;
nums[s] = arr[i];
}
}
4. 两个数组的交集
给定两个数组,编写一个函数来计算它们的交集
注意:输出结果中每个元素出现的次数,应与元素在两个数组中出现次数的最小值一致

- 思路1:
对排序后的数组遍历比较 - 思路2:
哈希表
public int[] intersect(int[] nums1, int[] nums2) {
Arrays.sort(nums1);
Arrays.sort(nums2);
int len1 = nums1.length;
int len2 = nums2.length;
int i=0,j=0,index=0;
int[] res = new int[len1>len2?len2:len1];
while(i<len1 && j<len2){
if(nums1[i]<nums2[j]){
i++;
}else if(nums1[i]>nums2[j]){
j++;
}else{
res[index] = nums1[i];
i++;
j++;
index++;
}
}
return Arrays.copyOfRange(res,0,index);
}
5. 数组加一
给定一个由整数组成的非空数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
这个解法的精妙之处在于如果位置上的数+1后无进位,就直接返回,否则向前进位继续+1
public int[] plusOne(int[] digits) {
int len = digits.length;
for(int i=len-1;i>=0;i--){
digits[i]++;
digits[i] = digits[i] % 10;
if(digits[i]!=0){
return digits;
}
}
digits = new int[len+1];
digits[0] = 1;
return digits;
}
6. 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序
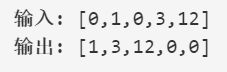
双指针法:一个指针遍历所有元素,一个记录不为0元素的索引,做法与第一题类似
public void moveZeroes(int[] nums) {
int len = nums.length;
int cur = 0;
int count = 0;
for(int i=0;i<len;i++){
if(nums[i]==0){
count++;
}else{
nums[cur++] = nums[i];
if(count!=0){
nums[i] = 0;
}
}
}
return;
}
7. 两数之和
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素不能使用两遍
思路:利用哈希表存放已有元素的值和索引
public int[] twoSum(int[] nums, int target) {
HashMap<Integer,Integer> map = new HashMap<>();
for(int i=0;i<nums.length;i++){
if(map.containsKey(target-nums[i])){
return new int[]{i,map.get(target-nums[i])};
}
map.put(nums[i],i);
}
throw new IllegalArgumentException("No two sum solution");
}
8. 有效的数独
判断一个 9x9 的数独是否有效。只需要根据以下规则,验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
public boolean isValidSudoku(char[][] board) {
//记录数字及其出现次数的表
int[][] rows = new int[9][9];
int[][] cols = new int[9][9];
int[][] cells = new int[9][9];
for(int i=0; i<board.length; i++){
for(int j=0; j<board[i].length; j++){
if(board[i][j]!='.'){
int num = board[i][j]-'0';
//行的判断
if(rows[i][num-1]==1)return false;
rows[i][num-1]++;
//列的判断
if(cols[j][num-1]==1)return false;
cols[j][num-1]++;
int cell = (i/3) * 3 + (j/3);
//九宫格的判断
if(cells[cell][num-1]==1)return false;
cells[cell][num-1]++;
}
}
}
return true;
}
9. 90°旋转矩阵
给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度
你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
public void rotate(int[][] matrix) {
int n = matrix.length;
// 1.矩阵转置
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
int tmp = matrix[j][i];
matrix[j][i] = matrix[i][j];
matrix[i][j] = tmp;
}
}
// 2.每行翻转
for (int i = 0; i < n; i++) {
for (int j = 0; j < n / 2; j++) {
int tmp = matrix[i][j];
matrix[i][j] = matrix[i][n - j - 1];
matrix[i][n - j - 1] = tmp;
}
}
}
总结
以上的数组算法题涉及到的内容有:双指针,贪心,排序,位运算,哈希表,二维矩阵,要熟练解决这些问题要靠平时多练
