1:排序算法分为如下5类:
- 插入排序:普通插入排序,shell排序等;
- 选择排序:普通选择排序,堆排序;
- 交换排序:冒泡法,快速排序;
- 归并排序:
- 基数排序。
待排数据为:9,6,2,3,10,有小到大排列;下面来实现上面的各种排序算法
2:插入排序(希尔排序)
基本插入排序:每次将一个待排序的数据元素,插入到前面已经排好序的数列中的适当位置,使数列依然有序;直到待排序数据元素全部插入完为止。
稳定排序:指待排序序列中可能存在两个或两个以上关键字相等的记录。排序前的序列中Ri领先于Rj(即i 希尔排序:是一种经过改进的插入排序算法。 希尔排序基本思想:先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率上比前两种方法有较大提高。具体做法:首先确定一组增量d0,d1,d2,d3,...,dt-1()其中n>d0>d1>...>dt-1=1),对于i =0,1,2,...,t-1,依次进行下面的各趟处理:根据当前增量di将n个元素分成di个组,每组中元素的下标相隔为di;再对各组中元素进行直接插入排序。 选择排序:每一次都是从待排序的数据元素中选出最小(或最大)的一个元素,顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。 堆排序:是一树形选择排序,在排序过程中,将R[1..N]看成是一颗完全二叉树的顺序存储结构,利用完全二叉树中双亲结点和孩子结点之间的内在关系来选择最小的元素。 交换排序:两两比较待排序记录的关键字,发现两个记录的次序相反时即进行交换,直到没有反序的记录为止。 首先来看著名的交换排序算法:冒泡法。冒泡法的排序思想是:从第n个元素(a[n-1])开始,扫描数组,比较相邻两个元素,如果次序相反则交换。如此反复,直到没有任何两个违反相反原则的元素 快速排序:在当前无序区R[1..H]中任取一个数据元素作为比较的“基准”(不妨记为X,R[1]),用此基准将当前无序区划分为左右两个较小的无序区:R[1..I-1]和R[I+1..H],且左边的无序子区中数据元素均小于等于基准元素,右边的无序子区中数据元素均大于等于基准元素,而基准X则位于最终排序的位置上,即R[1..I-1]≤X≤RI+ 1..H,当R[1..I-1]和R[I+1..H]均非空时,分别对它们进行上述的划分过程,直至所有无序子区中的数据元素均已排序为止。 找一个数X(比如头一个元素)做基准,右边比X小的移动到左边,左边比X大的移动到右边,最后空出的位置就是X自己的位置 快速排序的时间复杂度为O(nlogn),最坏情况为O(n^2)。对于大的、乱数序列一般相信是最快的已知排序。待排记录序列按关键字顺序有序时,直接插入排序和起泡排序能达到O(n)的时间复杂度,而对于快速排序而言,这是最不好的情况。对于很小的数组(如N<=20),快速排序不如插入排序好。 查找:将表中记录的关键字与查找关键字比较,如果两者相等,则查找成功,返回查找位置。 包含:链表查找,数组查找,二叉树查找,hash 折半查找:又叫二分查找,首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。 注意:折半查找必须满足两个条件:一,元素必须是连续存储;二,元素必须有序。时间复杂度:O(logn) Hash表用于存放key-value数据。比如一个学生的成绩,那么学生的学号可以当做key,成绩当做value,存放与hash表中。 Hash查找必须提供一个Hash函数,用于通过Key来计算数据存放在hash表中的位置。一般hash函数可以设计为key%N,其中N为hash表中元素的个数(一般为质数)。 假如HASH表的大小为N,那么Hash函数为:Hash(key)=key%N 当对于不同的两个key,计算出来的hash值可能相同,在相同的时候,就叫做hash冲突。解决hash冲突的方法不止一种,比如通过链式法解决,即将所有含有相同hash值的数据存放在同一个链表中,而将链表的头结点存放在HASH表中。 所谓hash查找,就是通过对应的key,按照hash函数,计算出数据在hash表中的位置。Hash查找的复杂度为O(1),所以具有较高的查找效率。//基本插入排序
//基本插入排序的时间复杂度为O(n^2),是一种稳定排序算法
void insert_sort(int a[], int n) {
int i, j, tmp;
for(int i=1; i//希尔排序的实现算法:
//希尔排序的复杂度为:O(n^1.25),它不是稳定排序。
void shellsort(int a[], int n) {
int i, j, gap, tmp;
gap = n/2;
while (gap > 0) {
for (i = gap + 1; i <= n; i++) {
j = i - gap;
while (j > 0) {
if (a[j] > a[j+gap]) {
tmp = a[j];
a[j] = a[j+gap];
a[j+gap] = a[j];
} else {
j = 0;
}
}
}
gap /= 2;
}
}
3:选择排序(堆排序)
//简单选择排序
//时间复杂度为O(n^2),它是不稳定排序。
void selectsort(int a[], int n) {
int i, j, k, tmp;
for (i = 0; i < n-1; i++) {
k = i;
for (j = i + 1; j < n; j++) {
if (a[j] < a[k])
k = j;
}
if (k != i) {
tmp = a[i];
a[i] = a[k];
a[k] = tmp;
}
}
}
//堆排序
//时间复杂度为O(nlogn),是不稳定排序
void sfilter(int a[], int l, int m) {
int i, j x;
i = l;
j = 2 * i;
x = a[i];
while ( j <= m) {
if (j < m && a[j] < a[j+1])
j++;
if (x < a[j]) {
a[i] = a[j];
i = j;
j = 2 * i;
} else {
j = m + 1;
}
}
a[i] = x;
}
void heapsort(int a[], int n) {
int i, w;
for (i = n/2; i >= 1; i--)
sfilter(a, i, n);
for (i = n; i >= 2; i--) {
w = a[i];
a[i] = a[1];
a[1] = w;
sfilter(a, 1, i - 1);
}
}
4:交换排序(冒泡排序/快排)
//冒泡排序:
//时间复杂度为O(n^2),它是稳定排序
void bubble_sort(int a[], int n) {
int i, j, tmp;
for (i = 0; i < n-1; i++) {
for (j = n-1; j >= i+1; j--) {
if (a[j] < a[j-1]) {
tmp = a[j];
a[j] = a[j-1];
a[j-1] = tmp;
}
}
}
}
void quickSort(int a[],int left,int right) {
int i,j,temp;
i=left;
j=right;
temp=a[left];
if(left>right)
return;
while(i5:排序时间复杂度空间复杂度比较
排序算法
平均时间
最坏情况
辅助存储
是否是稳定算法
简单排序
O(n^2)
O(n^2)
O(1)
快速排序
O(nlogn)
O(n^2)
O(logn)
堆排序
O(nlogn)
O(nlogn)
0(1)
归并排序
O(nlogn)
O(nlogn)
O(n)
基数排序
O(d(n+rd))
O(d(n+rd))
O(rd)
6:查找(折半查找/HASH查找)
6.1: 折半查找
//折半查找算法:
//a为存放数据的有序表,n为数据元素个数,k为要查找的元素
int bin_search(int a[], int n, int k) {
int low, high, mid, i;
low = 0;
high = n-1;
while (low <= high) {
mid = (low + high)/2;
if (a[mid] < k)
low = mid + 1;
else if (a[mid] > k)
high = mid - 1;
else {
return mid;
}
}
return -1;
}
//递归版本:
int iter_biSearch(int data[], const int x, int beg, int last) {
int mid = -1;
mid = (beg + last) / 2;
if (x == data[mid]) {
return mid;
} else if (x < data[mid]) {
return iter_biSearch(data, x, beg, mid - 1);
} else if (x > data[mid]) {
return iter_biSearch(data, x, mid + 1, last);
}
return -1;
}
int bin_search2(int a[], int n, int k) {
return iter_biSearch(a,k,0,n-1);
}
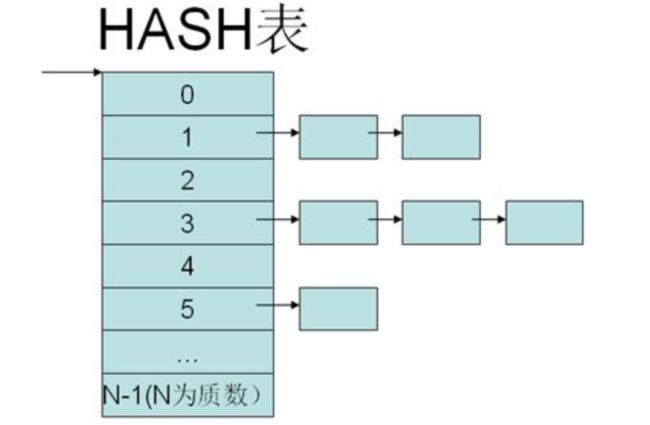
6.2:Hash表
6.3:二叉搜索树查找
typedef struct _node {
int data;
struct _node *left;
struct _node *right;
} node, btree;
btree *search(btree *b, int x) {
if (b == NULL) {
return NULL;
} else {
if (b->data == x) {
return b;
} else if (x < b->data) {
return (search(b->left));
} else {
return (search(b->right));
}
}
}