「数论」——1——【整除】

整除：

设a是非零整数，b是整数。如果存在一个整数q，使得b=a×q，那么就说b可被a整除,记作a|b，且称b是a的倍数，a是b的约数（因子）。例如3|12 ,21|63。整除具有以下的性质：

1、如果且，那么

2、 且   等价与对任意的整数x和y，有

3、设   ,那么

4、如果a和b互质,那么   a|n  ,  b|n  ->  (a*b)|n  

5、若b=q*d+c，那么d|b的充要条件是d|c

 

推论：

• 若2能整除a的最末位（约定0可以被任何数整除）.2|a

• 若4能整除a的最后两位，则4|a

• 若8能整除a的最后三位，则8|a

• 若3能整除a的各位数字之和，则3|a

• 若9能整除a的各位数字之和，则9|a

• 若11能整除a的偶数位数字之和 与 奇数位数字之和 的差，则11|a

• 若7、11、13整除的数的特征是：这个数的末三位数与除末三位数
  数字组成的数之差能被7、11、13整除，则  7|a,  11|a  ,  13|a

---

以上的推论我都给出证明：

1、若2能整除a的最末位（约定0可以被任何数整除）.2|a

        虽然说这个是小学知识，但是也可以用我们的同余模技术来解释。

         任何一个数，个位数为：0、2、4、6、8都能被2整除。

         解释：以个位数以2为例

         ＊＊＊＊＊＊2=（＊＊＊＊＊＊）* 10 + 2

         同余式中，若%2==0证明能被整除：

        （＊＊＊＊＊＊2）%2=【（＊＊＊＊＊＊）* 10 + 2】%2

                                            = 【（＊＊＊＊＊＊）* 10 】%2+【 2%2】

                                            = 【0】+【0】=0

2、若4能整除a的最后两位，则4|a

         像上面的式子：照葫芦画瓢即可。

         解释：以12结尾为例：

         ＊＊＊＊＊12=（＊＊＊＊＊）* 100 + 12

         同余式中，若%4==0证明能被整除：

        （＊＊＊＊＊12）%4 =【（＊＊＊＊＊）* 100 + 12】%4

                                            = 【（＊＊＊＊＊）* 100 】%4+【 12%4】

                                            = 【0】+【0】=0

3、若8能整除a的最后三位，则8|a

         像上面的式子：照葫芦画瓢即可。

         解释：以128结尾为例：

         ＊＊＊＊128=（＊＊＊＊）* 1000+ 128

         同余式中，若%8==0证明能被整除：

        （＊＊＊＊128）%8=【（＊＊＊＊）* 1000 + 128】%8

                                         = 【（＊＊＊＊）* 1000 】%8+【 128%8】

                                         = 【0】+【0】=0

4、若3能整除a的各位数字之和，则3|a

       这个就不能简单来处理了，但是这个问题挺好玩的。

       我们知道：10%3=1，100%3=1，1000%3=1

       那么我们以369123为例：

       369123=[3*1000000]%3+[6*100000]%3+[9*1000]%3+[1*100]%3+[2*10]%3+[3*1]%3

                   =( [0] + [0] + [0] + [1] + [2] + [0] )%3

                   =(  3  )%3

                   =0

      我们通过这个对每一位处理后我们就发现，其实归根结底还是一个问题：

      我们把每一位的数字用基数表示法来表示：3*100+2*10+1*1=321

      然后我们对于每一位100来模3后，最后   ：321%3=（3+2+1）%3

      只要每一位上的数字之和与3的倍数有关系即可：321%3=6%3=0

5、若9能整除a的各位数字之和，则9|a

      9|a：这个也是3|a的一个延伸拓展后的一个结论吧。

      我们知道1000%9=1，100%9=1，10%9=1

      然后任何的一个数都用基数表示法来表示，后来会发现：

      6654321%9=（6+6+5+4+3+2+1）=27%9=0

6、若11能整除a的偶数位数字之和 与 奇数位数字之和 的差，则11|a

     11|a，稍微有一点难证明。

     我们知道10%11=10，同时10=11-1 ，（11-1）%11 = -1

7、若11能整除a的偶数位数字之和 与 奇数位数字之和 的差，则11|a 

     这里运用到的同余公式：

     1、（a+b）%c=（a%c + b%c）%c 

     2、（ a*b）%c=（a%c）*（b%c）

    

    

                           

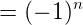                      其中（n为第几位数，如 n=2 ，即是百位数）

    如：718397=（7-3+8-3+9-7）%11 =  11%11 = 0

8、若7、11、13整除的数的特征是：这个数的末三位数与除末三位数
数字组成的数之差能被7、11、13整除，则  7|a,  11|a  ,  13|a 。

     这里运用到的同余公式：

     1、（a+b）%c=（a%c + b%c）%c 

     2、（ a*b）%c=（a%c）*（b%c）

     首先我们需要知道一回事，7*11*13=1001

     然后每一个超过三位数的数字都可以表示成：

     （ａｂｃｄｅｆｇｈ）＝（ａｂｃｄｅ＊１０００）＋（ｆｇｈ）

     因为（１０００）％１００１＝（１００１－１）％１００１

                                                    ＝（１００１％１００１）－（１％１００１）

                                                    ＝（０－１）％１００１＝－１

     所以有：　     

　（ａｂｃｄｅｆｇｈ）％１００１＝（ａｂｃｄｅ＊１０００）＋（ｆｇｈ）

                                                    　  ＝（（－ａｂｃｄｅ）＋ｆｇｈ）％１００１

　　例如: 45672627%1001=（45672-627）%1001=（1001*45）%1001=0

---

这些都是最基础的数论问题，谈论到整除一定涉及到余数的应用。

我们先插入一下（同余与模算术）：

以上的推论都基于一个定理：同余与模

主要在紫书-刘汝佳·《算法竞赛入门经典（第二版）》上也涉及到了。

• (a+b)%mod=( a%mod + b%mod )%mod

• ( a-b )%mod=( a%mod - b%mod+mod)%mod;

• a*b%mod=( a%mod)*(b%mod)%mod

以上三条式子都满足分配率，等会介绍除法！！！

中间插入一下：

---

HDU——1212 「大整数模除」

输入正整数n和m，输出n MOD m 的值。 

Big Number

---

Problem Description：

As we know, Big Number is always troublesome. But it's really important in our ACM. And today, your task is to write a program to calculate A mod B.

To make the problem easier, I promise that B will be smaller than 100000.

Is it too hard? No, I work it out in 10 minutes, and my program contains less than 25 lines.
 

---

Input：

The input contains several test cases. Each test case consists of two positive integers A and B. The length of A will not exceed 1000, and B will be smaller than 100000. Process to the end of file.
 

---

Output

For each test case, you have to ouput the result of A mod B.
 

---

Sample Input：

2 3
12 7
152455856554521 3250
 

---

Sample Output

2
5
1521
 

---

#include
#include
using namespace std;
int main()
{
    char n[100050];
    int m;
    while(scanf("%s%d",n,&m)!=EOF){
        int len = strlen( n ) ;
        int ans = 0;
        for( int  i = 0; i < len ; i++){
            ans=(int)( ( ( long long ) ans*10 +n[i]-'0')%m );
        }
        printf("%d\n",ans);
    }
    return 0;
}

 

---

HDU_1061 「幂取摸」

输入n,m 输出n^m%10的值。

Rightmost Digit

---

Problem Description

Given a positive integer N, you should output the most right digit of N^N.
 

---

Input

The input contains several test cases. The first line of the input is a single integer T which is the number of test cases. T test cases follow.
Each test case contains a single positive integer N(1<=N<=1,000,000,000).

---

Output

For each test case, you should output the rightmost digit of N^N.
 

---

Sample Input

2
3
4
 

---

Sample Output

7
6

---

Hint

In the first case, 3 * 3 * 3 = 27, so the rightmost digit is 7.
In the second case, 4 * 4 * 4 * 4 = 256, so the rightmost digit is 6.

---

应用在快速幂上的幂取摸。

#include
typedef long long ll;
const ll mod=10;
ll qpow(ll a,ll b){
    ll ans=1;
    while(b){
        if(b&1) ans=((ans%mod)*(a%mod))%mod;
        a=((a%mod)*(a%mod))%mod;
        b>>=1;
    }
    return ans;
}
int main()
{
    ll T,n,ans;
    scanf("%lld",&T);
    while(T--){
        scanf("%lld",&n);
        ans=qpow(n,n);
        printf("%lld\n",ans);
    }
    return 0;
}

---

「模线性方程组」

输入正整数a,b,n,解方程:      

同余。  的含义是" a 和 b 关于模n同余 ",即 a mod n = b mod n .

不难看出      的充要条件 是a-b是 n的整数倍。

这样，原来的方程就可以理解成 ：ax-b是 n 的正整数倍。设这个“ 倍数 ”为y，则 ax-b=by;

移项得：ax-ny=b,这恰好就是求解拓展欧几里德。

但是 b=1时, 的解称为 a 关于模n 的逆元，它类似于实数运算的倒数的概念，

ax-ny=1 要有解的话，必须满足通解。gcd( a, n )=1 也就是说这个a 和 n 必须是互质.

在满足这个前提下， 只有唯一解。同余方程的解指的是一个等价类。

poj 2891

---

整除的尾数（整除的应用）

Problem Description

一个整数，只知道前几位，不知道末二位，被另一个整数除尽了，那么该数的末二位该是什么呢？
 

---

Input

输入数据有若干组，每组数据包含二个整数a，b（0  

---

Output

对应每组数据，将满足条件的所有尾数在一行内输出，格式见样本输出。同组数据的输出，其每个尾数之间空一格，行末没有空格。
 

---

Sample Input

200 40
1992 95
0 0
 

---

Sample Output

00 40 80
15
 

暴力枚举每一位0～99

#include
int main()
{
    int n,m;
    while(~scanf("%d%d",&n,&m),(n||m)){
        int ans[100],cnt=0;
        for(int i=0;i<=99;i++){
            if((n*100+i)%m==0){
                ans[cnt++]=i;
            }
        }
        for(int i=0;i

---

斐波那契的整除

---

Description

已知斐波那契数列有如下递归定义，f(1)=1,f(2)=1, 且n>=3,f(n)=f(n-1)+f(n-2)，它的前几项可以表示为1， 1，2 ，3 ，5 ，8，13，21，34…，现在的问题是想知道f(n)的值是否能被3和4整除，你知道吗？

---

Input

输入数据有若干组，每组数据包含一个整数n（1< n <1000000000）。

---

Output

对应每组数据n，若 f(n)能被3整除，则输出“3”； 若f(n) 能被4整除，则输出“4”；如果能被12整除，输出“YES”；否则输出“NO”。

---

Sample Input

4
6
7
12

---

Sample Output

3
4
NO
YES

找规律即可：

#include
int main()
{
    int n;
    while(~scanf("%d",&n)){
        if(n%12==0){
            printf("YES\n");
        }else if(n%4==0){
            printf("3\n");
        }else if(n%6==0){
            printf("4\n");
        }else{
            printf("NO\n");
        }
    }
    return 0;
}

---

【数论】教堂

题目描述

ROMA城中有一些古典的印度式建筑，这些建筑和周围的欧洲建筑风格格格不入。这些伪装成教堂的建筑其实是某国特工的基地。Tomas接受了一项任务，就是从某个教堂出发，逐个访问这些教堂，搞清楚每一个教堂的内部结构，并回到出发的地方。这些教堂很有规律地构成了一个m*n的矩形，每个教堂和它的八个方向的教堂有直接的路径相连。水平或垂直方向相邻的教堂之间的路程均为1。请问Tomas至少需要走多远的路，才能完成这个危险而艰巨的任务呢？

输入

输入一行两个整数m和n（m，n≤10000）

输出

输出一行一个实数，表示最少需要走的路程，保留两位小数。

样例输入

2 3

样例输出

6.00
 

通过小数据进行找规律，如 (2,3)、( 2, 4 )、(3,2)、(3,3)、(3,4)、(3,5)、(4,2)、(4,3)、注意要1的情况。

#include
#include
int main()
{
    double ans;
    int n,m;
    scanf("%d%d",&n,&m);
    if((n==1)||(m==1)){
        ans=(n+m-2)*2;
    }else if((n&1)&&(m&1)){
        ans=n*m;
        ans-=1;
        ans+=sqrt(2);
    }else{
        ans=n*m;
    }
    printf("%.2lf\n",ans);
    return 0;
}

【数论】密码

题目描述：

有一个密码箱，0到n-1中的某些整数是它的密码。且满足：如果a和b都是它的密码，那么(a+b)%n也是它的密码(a,b可以相等，%表示整除取余数)，某人试了k次密码，前k-1次都失败了，最后一次成功了。
问：该密码箱最多有多少不同的密码。

输入

第一行两个整数分别表示n，k（1≤k≤250000，k≤n≤1014）。第二行为k个用空格隔开的非负整数，表示每次试的密码。数据保证存在合法解。

输出

输出一行一个数，表示结果。

样例输入

42   5
28   31   10   38   24

样例输出

14

---

 题意：

这个题目，太短了，我总有些迷糊，我就告诉大家这个题目的意思吧：

有一个密码箱，它有多个密码，每一个密码是一个整数，比如 235，是一个数。

然而在N个数里面中，主人公尝试了K遍终于把答案给他试出来了，

所以说第K个数就是密码之一。

?????

为什么是之一呢，题目告诉我，z=(x+y)%n,其中x,y,z都是密码。

然后要你输出，如果答案有多个，输出最多的那种可能。

题解：

后来我就发现，从z=(x+y)%n出发，其实题目就是要我们找到某一个符合要求的，

且是最小的一个因子，(因子？？？？)就是第K个数的因子。

比如从示例入手：

42   5

28   31   10   38   24

24的因子有：1，2，3，4，6，8，12，24;

然后在1~k-1都不满足，也就是说，其中答案所要的因子，不能是前K-1个数任何一个的因子。

28：1，2，4

31:   1

10:   1 , 2

38：1，2

然后大家发现，现在能用的因子只有：3，6，8，12，24.

我们想要答案尽可能多，所以我们选择的就是3

42/3=14.（/ 是整除，即向下取整）

这个解法：我还真的是看了答案才知道他是怎样处理多个问题的？？?
问题1：我们需要他的所有因子，而不是质因数分解

问题2：我们怎么把前K-1个数处理好呢，我们需要处理，不能和K的因子有关系？？

 

首先我们需要分析出一个小细节：

那就是 K既然是答案之一，那么gcd(n,K)肯定也是答案之一。

到时再补充：

 

问题1：其实想用一个根号的复杂度枚举所有他的因子即可。

问题2：不看答案真没想到，其实前K-1个数，他的作用只是看看和K的GCD罢了。

所以我们先预处理一波，（这个我是想到的，但是没想过是直接预处理。）

再对每一个因子，我们只是处理了最大公因数，可能有些更小的公因数被他覆盖了，

所以我们还需要一个cnt^2的复杂度来处理一下，其中(cnt<=17);因为  17! >1e15

最后扫一遍即可找到答案。

#include
using namespace std;
const int N=3e6+10;
typedef long long ll;
ll gcd(ll a,ll b ){
    return a%b==0?b:gcd(b,a%b);
}
ll n,k,K;
ll a[N],q[N],cnt=0;
ll vis[N]={0};
int main()
{
    scanf("%lld%lld",&n,&k);
    for(int i=1;i

 

---

参考书籍：

哈尔滨工业大学出版社·陈宇·《ACM——ICPC程序设计系列-数论及应用》

东南大学出版社·林厚从·《信息学奥赛之数学一本通》