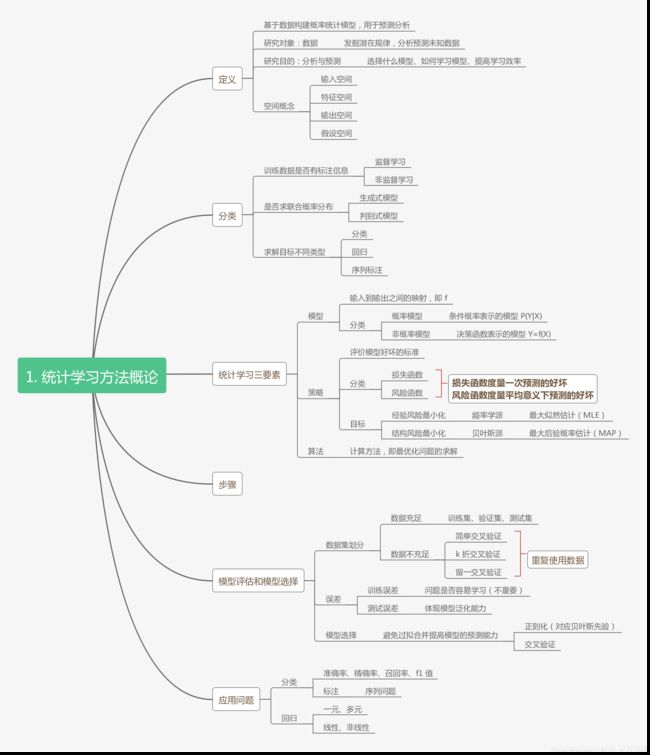
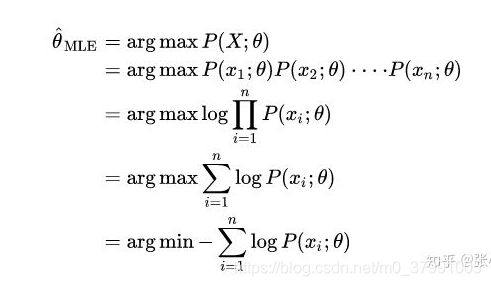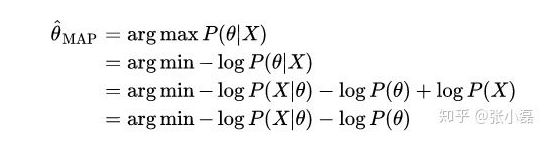第一章 统计学习方法概论总结
文章目录
- 空间概念
- 最大似然估计(MLE)和最大后验概率估计(MAP)
- 正则化
- l1 正则化和 l2 正则化
- 生成模型和判别模型
空间概念
监督学习下
- 输入空间:输入所有可能取值的集合
- 输出空间:输出所有可能取值的集合
输入与输出空间可以是有限元素的集合,也可以是整个欧式空间
-
特征空间:所有特征向量(对实例的表示)存在的空间
-
假设空间:输入空间到输出空间映射的集合,即包含所有可能的模型的集合
有时候假设输入空间和特征空间是相同的空间,但有时候也假设他们是不同的空间,把实例从输入空间映射到特征空间。模型实际上都是定义在特征空间上的
最大似然估计(MLE)和最大后验概率估计(MAP)
- MLE对参数的 θ \theta θ 估计方法
- MAP对 θ \theta θ 的估计方法
所以MAP和MLE在优化时的不同就是在于增加了一个先验项 − l o g P ( θ ) -logP(\theta ) −logP(θ)
从数学表达式的角度来说,两者最大的区别就在这里:贝叶斯估计引入了先验概率,通过先验概率与似然概率来求解后验概率。而最大似然估计是直接通过最大化似然概率来求解得出的。最大似然估计没有考虑模型本身的概率,或者说认为模型出现的概率都相等。而贝叶斯估计将模型出现的概率用先验概率的方式在计算过程中有所体现。
- MLE简单又客观,但是过分的客观有时会导致过拟合(Over fitting)。在样本点很少的情况下,MLE的效果并不好。
- 贝叶斯估计最要命的问题是,实际应用场景中的先验概率不是那么好求,很多都是拍脑袋决定的。一旦是拍脑袋决定的,这玩意自然就不准;更有甚者,很多时候是为了方便求解生造出来一个先验。那既然这样,要这个先验还有什么卵用呢?所以频率派的支持者就揪住这点不放攻击贝叶斯派。
在现在看来,Frequentist与Bayesian这两派还将长期并存,在各自适合的领域发挥自己的作用。
正则化
正则化项可以取不同的形式。从贝叶斯估计角度看,正则化项对应于模型的先验概率,可以假设复杂的模型有较小的先验概率,简单的模型有较大的先验概率。
l1 正则化和 l2 正则化
为什么L1和L2正则化可防止过拟合
l1 相比于 l2 为什么容易获得稀疏解?
生成模型和判别模型
生成模型
联合概率分布 P ( X , Y ) P(X,Y) P(X,Y)——>条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)
P ( Y ∣ X ) = P ( X , Y ) P ( X ) P(Y|X)=\frac {P(X,Y)}{P(X)} P(Y∣X)=P(X)P(X,Y)
- 基本思想
首先建立样本的概率密度模型,再利用模型进行推理预测。要求已知样本无穷或尽可能的大。建立在bayes理论的基础之上
- 特点
主要是对后验概率建模,从统计的角度表示数据的分布情况,能够反映同类数据本身的相似度。
- 优点
由于产生式方法可以在联合分布空间插入变量、不变量、独立性、先验分布等关系的知识。因此,在联合分布空间,通用性(或称多面性)是其本质。这包括了系统中的未知的、观察到的、输入或输出变量,这就使得产生式概率分布成为一个非常灵活的建模工具。
- 缺点
产生式分类器需产生的所有变量的联合概率分布仅仅是分类任务的中间目标,对该中间目标优化的过程,牺牲了最终分类判别任务上的资源和性能,影响了最终的分类性能。
- 典型模型
朴素贝叶斯、隐马尔科夫
判别模型
直接学习条件概率 P ( Y ∣ X ) P(Y|X) P(Y∣X) 或者决策函数 f ( X ) f(X) f(X)
- 基本思想
有限样本条件下建立判别函数,不考虑样本的产生模型,直接研究预测模型。代表性理论为统计学习理论。
- 特点
寻找不同类别之间的最优分类面,反映的是异类数据之间的差异。
- 优点
- 相比纯概率方法或产生式模型,分类边界更灵活
- 能清晰的分辨出多类或某一类与其他类之间的差异特征,适用于较多类别的识别
- 判别模型的性能比产生模型要简单,比较容易学习
- 缺点
- 不能反映训练数据本身的特性。可以告诉你的是1还是2,但没有办法把整个场景描述出来
- 判别式方法在训练时需要考虑所有的数据元组,当数据量很大时,该方法的效率并不高
- 缺乏灵活的建模工具和插入先验知识的方法。因此,判别式技术就像一个黑匣子,变量之间的关系不像在产生式模型中那样清晰可见
当训练数据较少的时候Logistic Regression分类器的效果比较差,随着训练数据的增加其对测试数据的分类正确率快速增加。而NaiveBayes分类器对于训练数据的多少并不敏感,分类效果比较稳定。
参考链接
极大似然估计与最大后验概率估计
最大似然估计MLE与贝叶斯估计