倾向匹配得分PSM学习笔记
一直在想写倾向匹配得分PSM学习笔记,好好总结一下。但一直拖着,对倾向匹配得分法虽然思想比较理解,但没有系统地学习,所以这篇博客总结一下老师们的一些文章,在总结中学习,哈哈~
倾向匹配得分PSM学习笔记
- 1 产生背景
- 2 PSM基础介绍
- 2.1 倾向匹配原理
- 2.2 倾向匹配方法
- 2.2.1 局部匹配(local algorithms)
- 2.2.2 全局匹配(globalalgorithms)
- 2.3 倾向匹配效果检验
- 3 PSM在stata示例
- 3.1 安装及语法介绍
- 3.2 数据描述性统计
- 3.3 倾向匹配运行步骤
- 3.4 倾向匹配效果检验
- 3.4.1 均衡性检验
- 3.4.2 共同取值范围
- 3.4.3 核密度函数图
- 4 PSM的思考
1 产生背景
参考学习文章:【内容回顾】倾向性评分匹配
流行病学病因研究中,为了探讨某因素(处理或干预,后统称“处理因素”)与结局(如疾病)的关系,需要设立对照组进行比较。但对照组的重要特征是具备可比性,即除某因素外,其他因素相同,不会干扰处理因素和结局。
因为如果研究人群中存在一个或多个既与观察结局有关,又与处理因素有关的外来因素,那么就可能会掩盖或夸大所研究的处理因素与观察结局之间的联系。这种影响称之为混杂偏倚(confounding bias)或称混杂(confounding)。这些外来因素称为混杂因素(confounding factors)。
我们可以通过随机对照研究降低混杂因素,通过随机化分配研究对象,使混杂因素(或协变量)在处理组和对照组中的分布趋于平衡,然后分析处理因素与结局之间的关系。但受到实验条件限制,较难实现。
因而传统的控制混杂偏倚的方法包括在研究设计阶段进行配比,或在数据分析阶段按照混杂因素分层,或采用多因素数学模型进行调整等,使混杂因素(或协变量)在处理组和对照组中的分布趋于平衡,然后分析处理因素与结局之间的关系。
而倾向匹配得分(PSM)的原理大致如此。
2 PSM基础介绍
2.1 倾向匹配原理
PS由Rosenbaum和Rubin于1983年首次提出。它是多个协变量的一个函数,用于处理观察性研究中组间协变量分布不均衡的问题。PS是根据已知协变量的取值(Xi)而计算的第i 个个体分入观察组的条件概率(即根据个体的一些特征判定这个个体进入观察组的概率):

这里G 表示组别或干预因素,G=1 表示该个体在观察组,G=0 表示该个体在对照组;X 为协变量向量x=(x1,x2,…,xm),或者称为特征向量。
若PS用传统的logistic回归或probit回归方法计算,即以组别G 为因变量,以所要控制的因素为自变量建立logistic模型或者probit模型:
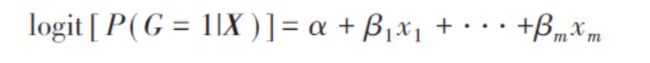
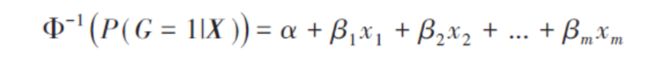
注意:个体的协变量(特征向量)的选取是依据研究项目自身抉择的。如判断一个公司能否IPO成功,那么它的协变量就可能包括ROA、SALE、SIZE等诸多变量
2.2 倾向匹配方法
2.2.1 局部匹配(local algorithms)
常用的局部匹配方法有最邻近匹配(nearest neighbor matching)、卡钳匹配(caliper matching)
(1) 最邻近匹配:将观察组中的每个个体,在对照组中寻找与其最接近的个体进行匹配,直到观察组中每个个体都找到匹配,称为最邻近匹配。
(2)卡钳匹配:如果两个个体的PS差值在事先设定的某范围(称为卡钳值(caliper))内才能进行匹配,称为卡钳匹配。Austin的蒙特卡洛模拟结果表明,最合适全局匹配法将匹配问题转化为运筹学中网络流问题(network flows),此时观察组和匹配的对照组个体PS差值并不是最小的,但是能保证匹配集PS总体差值的最小化的卡钳值是取两组倾向指数标准差的20%,或者取两组间PS绝对差值(卡钳值)为0.02或0.03等。
(3)此外马氏距离法、核匹配法等
2.2.2 全局匹配(globalalgorithms)
全局匹配法将匹配问题转化为运筹学中网络流问题(network flows),此时观察组和匹配的对照组个体PS差值并不是最小的,但是能保证匹配集PS总体差值的最小化
我们常用到的是局部匹配方法
2.3 倾向匹配效果检验
(1)PS 分布抖点图( jitter plot)
PS 分布抖点图( jitter plot) ,表示处理组与对照组间匹配与未匹配者( unmatched treatment units:未匹配处理组,matched treatment units: 已匹配处理组,matched control units: 已匹配对照组,unmatched control units: 未匹配对照组) PS 的分布,从而了解匹配的效果。

(2)PS 分布直方图
表示处理组与对照组间匹配前后( raw treated、raw control、matched treated、matched control 分别指匹配前处理组与对照组以及匹配后处理组与对照组) PS 值的分布,通过此图可看出处理与对照组匹配均衡性及匹配效果。

(3)PS模型变量的QQ 图
表示处理组与对照组间各个变量的PS 分布,可看出单个变量的匹配前后的均衡情况。如年龄变量( age) 的PS 由匹配前的非正态分布变为匹配后的正态分布,说明年龄变量匹配效果较好。

(4)PS共同支持域图
两组倾向评分重叠区范围常称为共同支持域,共同支持域的大小是影响具体匹配方法估计效果的一个重要因素。如果两组没有共同支持域,表明两组完全没有可比性,也无法进行倾向评分分析。

3 PSM在stata示例
学习文章:
一文读懂倾向匹配得分Stata及R操作应用
倾向得分匹配(PSM)操作过程与问题反思
3.1 安装及语法介绍
(1)安装命令
ssc install psmatch2, replace
(2)语法格式
help psmatch2
psmatch2 depvar # depvar因变量
[indepvars] # indepvars表示协变量;
[if exp] [in range]
[, outcome(varlist) # outcome(varlist)表示结果变量;
pscore(varname)
neighbor(integer) # neighbor(1)指定按照1:1进行匹配,如果要按照1:3进行匹配,则设定为neighbor(3);
radius caliper(real) # radius表示半径匹配
mahalanobis(varlist) # 马氏匹配 (Mahalanobis matching)
ai(integer) population altvariance
kernel llr kerneltype(type) bwidth(real) spline # 样条匹配 (Spline matching)
nknots(integer) common trim(real) noreplacement
descending odds index
logit ties quietly w(matrix) ate] # logit指定使用logit模型进行拟合,默认的是probit模型;
3.2 数据描述性统计
(1)数据来源
国家支持工作示范项目( National Supported Work,NSW ) 数据
数据网址如下:http://economics.mit.edu/faculty/angrist/data1/mhe/dehejia


(2)变量定义
use nswre74.dta,replace
* 变量处理
drop age2
gen u74 = 1 if re74==0 //当在1974年失业,u74=1
replace u74 = 0 if u74 ==.
gen u75 = 1 if re75==0 //当在1975年失业,u74=1
replace u75 = 0 if u75 ==.
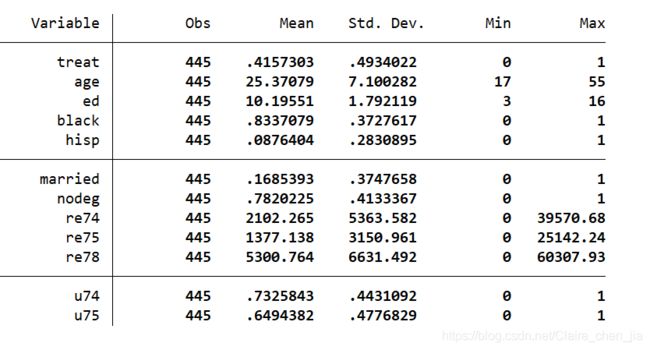
describe
treat:接受培训(处理组)表示1,没有接受培训(控制组)表示0
age:年龄
educ:受教育年数
black:种族虚拟变量,黑人时,black=1
hsip:民族虚拟变量,西班牙人时,hsip=1
married:婚姻状况虚拟变量,已婚,marr=1,否则为0
nodegree: 高中学历以上则为1,否则为0
re74:1974年实际工资
re75:1975年实际工资
re78:1978年实际工资
u74:当在1974年失业,u74=1,否则为0
u75:当在1975年失业,u75=1,否则为0

(3)描述性统计
在这里插入代码片
3.3 倾向匹配运行步骤
(1)生成随机数种子,然后排序,保证样本是随机排序
set seed 20180105 //产生随机数种子
gen u=runiform()
sort u //排序
(2)倾向匹配得分组别和特征向量设置
global v1 "treat" // 处理组
global v2 "age ed black hisp married re74 re75 u74 u75" // 匹配的特征向量(协变量)x
global x "`v1' `v2' "
(3)以logit进行倾向得分匹配回归
psmatch2 $x, out(re78) neighbor(1) ate ties logit common // 1:1 匹配 以组别treat 为因变量,以所要控制的因素为自变量,以re78为结果变量,建立logit模型
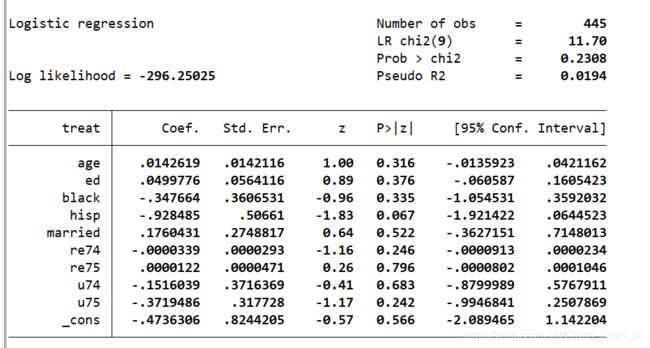

我们主要关注的是ATT(Average treatmenteffect for the treated),它是来测度个体在干预状态下的平均干预效应,即表示个体i在干预状态下的观测结果与其反事实的差,称为平均干预效应的标准估计量。
根据ATT后面的t值,在匹配之前说明某一个政策实施有显著的差异;进行匹配之后,t值还是比较大的,说明这个政策的确有效果。一般而言,在5%的显著性水平上,t值大于1.96是显著的。
上表,匹配前处理组和控制组差异为1794.34238,并且 t 值为2.84,匹配后处理组和控制组差异「ATT」为1410.59158,并且 t 值为1.68。

上表列示了处理组和控制组在共同取值范围的情况,其中控制组249个样本都在共同取值范围内,而处理组有13个样本不在共同取值范围内,有183在共同取值范围内。
(4)亦可运用bootstrap获得ATT标准误
在统计分析中,样本较少,采用bootstrap,可以减少小样本偏误。
步骤:首先,从原始样本中可重复地随机抽取n个观察值,得到经验样本;然后采用PSM计算改经验样本的平均处理效果ATT;将第一步和第二步重复进行#次,得出#个ATT值;计算#个
ATT值的标准差。
bootstrap,reps (10) : psmatch2 $x ,out(re78) neighbor(1) ate ties logit common // 重复进行10次
**其他匹配方法
psmatch2 $x , out(re78) ate radius caliper(0.01) // 半径小于0.01的半径匹配方法
psmatch2 $x , out(re78) ate radius kernel // 核匹配
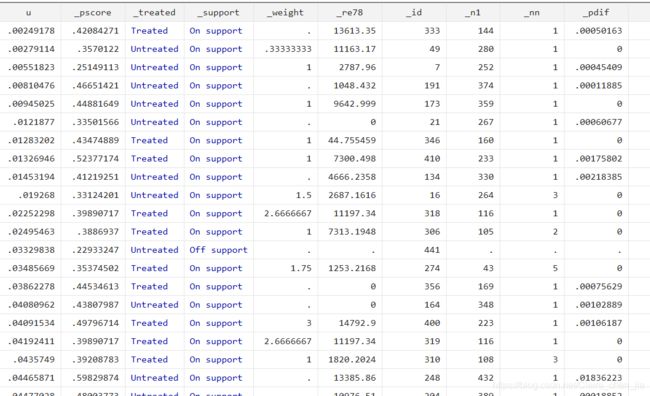
(6)查看新生成的变量
其中_pscore是每个观测值对应的倾向值;
_id是自动生成的每一个观测对象唯一的ID(事实上这列变量即是对_pscore排序);
_treated表示某个对象是否试验组;
_n1表示的是他被匹配到的对照对象的_id(如果是1:3匹配,还会生成_n2, _n3);
_pdif表示一组匹配了的观察对象他们概率值的差
_weight:代表匹配次数,在 1:1 非重复匹配下,_weight != . 表示匹配成功,且匹配成功时 _weight = 1。在 1:1 可重复匹配下,参与匹配的控制组 _weight 的取值可能为任意整数。
3.4 倾向匹配效果检验
倾向匹配效果检验,它是为了检验混杂因素(或协变量)在处理组和对照组中的分布是否趋于平衡
3.4.1 均衡性检验
pstest 命令主要考察匹配质量,以检验是否满足「平衡性假设 (balancing assumption)」。从下表可以看出,匹配后大多数变量标准化偏差 (%bias) 都比较小,而且 t 值都不拒绝处理组和控制组无系统性偏差的原假设。从下图也可以看出,所有变量的标准差在匹配后都缩小了。
pstest $v2, both graph // 比较对照组和控制组特征向量的差异
3.4.2 共同取值范围
psgraph
3.4.3 核密度函数图
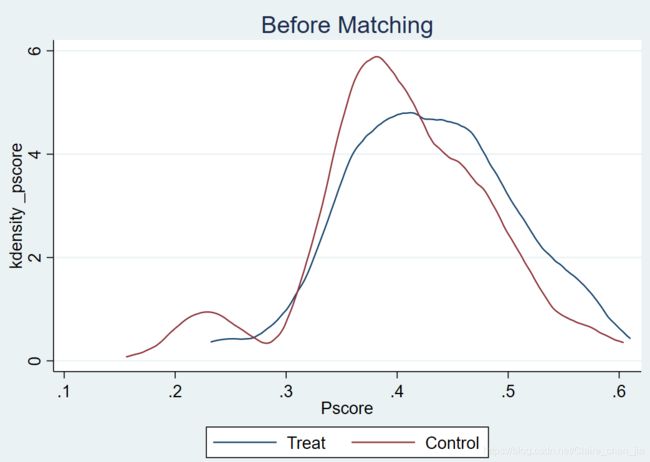
// 匹配前
twoway(kdensity _ps if _treat==1,legend(label(1 "Treat")))(kdensity _ps if _treat==0, legend(label(2 "Control"))),xtitle(Pscore) title("Before Matching")
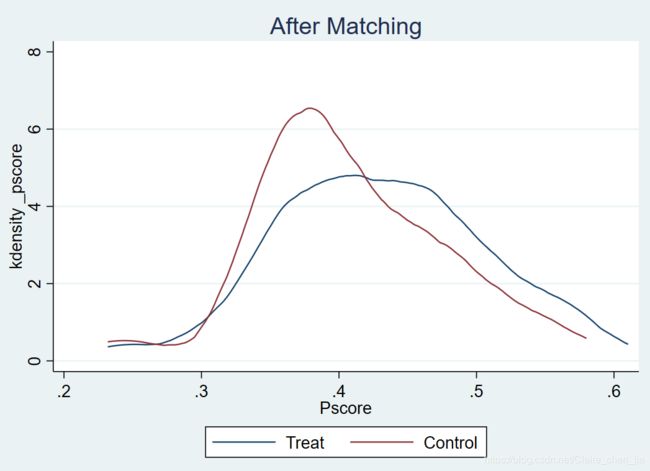
//匹配后
twoway(kdensity _ps if _treat==1,legend(label(1 "Treat")))(kdensity _ps if (_weight!=1&_weight!=.), legend(label(2 "Control"))),xtitle(Pscore) title("After Matching")
4 PSM的思考
思考是学习于:PSM:倾向得分匹配能解决内生性吗?
正如前文讲到PSM的初衷是为了是处理组和控制组的一些因素(干扰自变量和因变量)趋于平衡(或者说相似),使得减轻这些因素对结果的干扰,进而缓解内生性问题,如遗漏变量,自选择。
然而,虽然 PSM 和 MR 都是通过控制与被解释变量和处理变量相关的可观测变量来缓解选择偏差,但二者的差异也很明显,主要体现在三个方面。
其一, PSM 并不能完全解决由「选择偏差或遗漏变量」所导致的内生性问题,因为遗漏变量还是仍未进入模型等。
其二, PSM 不能被称为「准实验」,也无法模拟实验条件。
PSM 可以模拟实验条件,但它还是事后事件。尽管处理组和对照组的协变量平衡可能类似于实验条件,PSM 仍缺少实验的重要特征。首先,PSM 只是缓解了可观测变量的系统差异,不可观察变量的差异并未缓解。而实验通过随机分配,可以有效控制可观测和不可观察变量影响。其次,PSM 决定了哪些观测值进入分析的样本中。
其三, PSM 的外部有效性问题。
在「共同支撑假设 (Common Support)」无法满足或很牵强的情况下,PSM 会系统排除缺乏对照组的样本,进而使得样本代表性变差,影响结果的外部有效性。
觉得这篇文章[PSM:倾向得分匹配能解决内生性吗?]的示例也挺好的,所以也敲了一遍,有兴趣的可以去看看呀~
*-定义全局暂元
global indepvar LNASSET LEV ROA GROWTH BM AGE // 自变量
global fixvar i.indcode i.year // 固定效应
*-样本匹配
probit BIG4 $indepvar $fixvar, vce(cluster stkcd) // probit模型,估计选择四大的概率
est store Probit // 存储probit结果
predict pscore, p // 根据probit预测的概率,作为倾向得分匹配的估计基础
psmatch2 BIG4, pscore(pscore) outcome(ABSACC RESTATE) ///
common n(1) norepl cal(0.03) // 半径匹配(半径为0.03),且是1:1的不重复匹配
pstest $indepvar, both graph // 均衡性检验
psgraph // 共同取值范围
*-回归结果
*-Full Sample ABSACC
reg ABSACC BIG4 $indepvar $fixvar, cluster(stkcd) // 选择四大
est store ABSACC_F
*-Matched Sample ABSACC
reg ABSACC BIG4 $indepvar $fixvar [fweight=_weight], cluster(stkcd) // _weight是表示匹配次数,本例是1:1,所以是1,fweight 为「frequency weights」的简写,是指观测值重复次数的权重。
est store ABSACC_M
*-Full Sample RESTATE
reg RESTATE BIG4 $indepvar $fixvar, cluster(stkcd) // 财务重述
est store RESTATE_F
*-Matched Sample RESTATE
reg RESTATE BIG4 $indepvar $fixvar [fweight=_weight], cluster(stkcd)
est store RESTATE_M
*-结果对比
local m "Probit ABSACC_F ABSACC_M RESTATE_F RESTATE_M"
esttab `m', mtitle(`m') b(%6.3f) nogap drop(*.indcode *.year) ///
order(BIG4) s(N r2_p r2_a) star(* 0.1 ** 0.05 *** 0.01)
参考学习文章:
- 【内容回顾】倾向性评分匹配
- 一文读懂倾向匹配得分Stata及R操作应用
- 倾向得分匹配(PSM)操作过程与问题反思
- PSM:倾向得分匹配能解决内生性吗?