【论文笔记】Deep Residual Learning for Image Recognition
【论文笔记】Deep Residual Learning for Image Recognition
- 介绍
- 深度残差学习
- 残差学习
- Identity Mapping by Shortcuts
- 网络结构
- 实验
论文地址:https://arxiv.org/abs/1512.03385
译文地址:https://blog.csdn.net/wspba/article/details/57074389
介绍
该文章解决了深度学习中的退化问题:随着网络深度的增加,准确率达到饱和(不足为奇)然后迅速退化。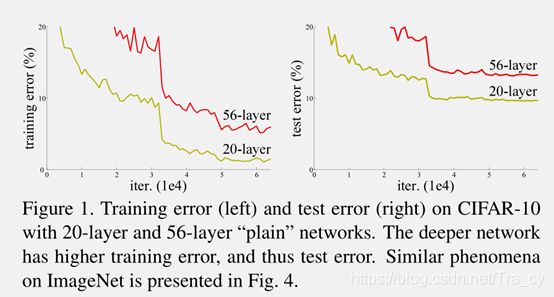
Fig.1 20层和56层的“plain”网络在CIFAR-10上的训练错误率(左)和测试错误率(右)。越深的网络在训练和测试上都具有越高的错误率。
上图所示,网络随着深度的增加(从20层增加到56层),训练误差和测试误差非但没有降低,反而变大了。然而这种问题的出现并不是因为过拟合(overfitting)。
照理来说,如果我们有一个浅层的网络,然后我们可以构造一个这样的深层的网络:前面一部分的网络和浅层网络一模一样,后面一部分的网络采用恒等映射(identity mapping),那么,深层网络的产生的误差至少不会比浅层网络的高。但是目前却不能找到一个更好的方法比用刚才的方法构造的网络效果要好。
本文提出了一种深度残差学习框架来解决退化问题。让这些层来拟合残差映射(residual mapping),而不是让每一个堆叠的层直接来拟合所需的底层映射(desired underlying mapping)。假设所需的底层映射为 H(x)H(x),我们让堆叠的非线性层来拟合另一个映射: F(x):=H(x)−xF(x):=H(x)−x。 因此原来的映射转化为: F(x)+xF(x)+x。我们推断残差映射比原始未参考的映射(unreferenced mapping)更容易优化。在极端的情况下,如果某个恒等映射是最优的,那么将残差变为0 比用非线性层的堆叠来拟合恒等映射更简单。
于是,作者就提出了deep residual learning framework。结构如下:

Fig.2 残差学习:一个构建块。
其实就是在原来网络的基础上,每隔2层(或者3层,或者更多,这篇文章作者只做了2层和3层)的输出F(x)上再加上之前的输入x。这样做,不会增加额外的参数和计算复杂度,整个网络也可以用SGD方法进行端对端的训练,用目前流行的深度学习库(caffe等)也可以很容易的实现。
该网络的优点:
- 即使很深的网络也容易优化
- 可以通过增加层来提高准确率,并且结果也大大优于以前的网络
深度残差学习
残差学习
将H(x)H(x)看作一个由部分堆叠的层(并不一定是全部的网络)来拟合的底层映射,其中xx是这些层的输入。假设多个非线性层能够逼近复杂的函数,这就等价于这些层能够逼近复杂的残差函数,例如, H(x)−xH(x)−x (假设输入和输出的维度相同)。所以我们明确的让这些层来估计一个残差函数:F(x):=H(x)−xF(x):=H(x)−x 而不是H(x)H(x)。因此原始函数变成了:F(x)+xF(x)+x。尽管这两个形式应该都能够逼近所需的函数(正如假设),但是学习的难易程度并不相同。
Identity Mapping by Shortcuts
作者提出的网络结构有如下2种情形:
- 当F和x相同维度时,直接相加(element-wise addition),公式如下:这种方法不会增加网络的参数以及计算复杂度。
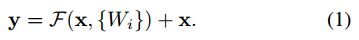
- 当F和x维度不同时,需要先将x做一个变换(linear projection),然后再相加,公式如下:Ws仅仅用于维度匹配上。
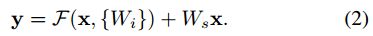
网络结构
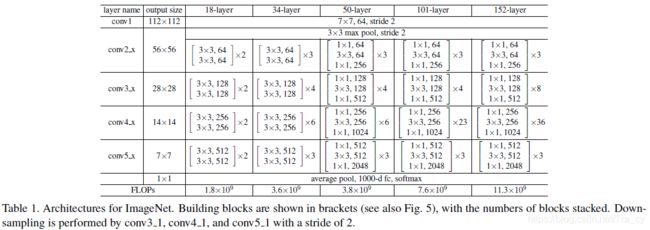
Plain网络:基于VGGNet,采用的卷积核为3x3,其中有两个设计原则,1)对于有相同的输出feature map尺寸,filter的个数相同;2)当feature map尺寸减半时,filter的数量加倍。下采样的策略是直接用stride=2的卷积核。网络最后末尾是一个global average pooling layer(不需要参数,参考http://www.cnblogs.com/hejunlin1992/articles/7750759.html)和一个1000的全连接层(后面接softmax)。
残差网络:在基准网络的基础上,插入了shortcut connections。当输入输出具有相同尺寸时,identity shortcuts可以直接使用(实线部分),就是公式1;当维度增加时(虚线部分),有以下两种选择:A)仍然采用恒等映射(identity mapping),超出部分的维度使用0填充;B) 利用1x1卷积核来匹配维度,就是公式2。对于上面两种方案,当shortcuts通过两种大小的feature map时,采取A或B方案的同时,stride=2。

Fig.3 对应于ImageNet的网络框架举例。 左:VGG-19模型 (196亿个FLOPs)作为参考。中:plain网络,含有34个参数层(36 亿个FLOPs)。右:残差网络,含有34个参数层(36亿个FLOPs)。虚线表示的shortcuts增加了维度。
实验
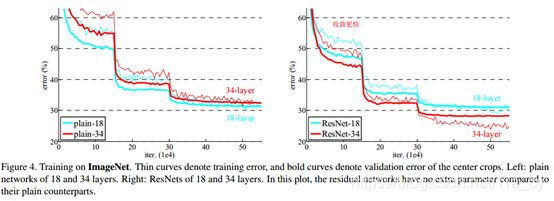
Fig.4 在ImageNet上进行训练。细曲线为训练错误率,粗曲线为使用中心crop时的验证错误率。左:18和34层的plain网络。右:18 和34层的ResNets。在这个图中,残差网络和对应的plain网络相比并没有增加额外的参数。
从上图左边,可以看出,plain-34网络不管是训练误差还是验证集上的误差,都要比plain-18要大,由于plain网络采用了BN来训练,并且作者也验证过前向传播或者反向传播中,信号并没有消失,因此说明出现了退化现象(到底为什么会出现这种情况,作者也还在研究之中)。
再看上图右边的残差网络,结合下面的表2,34层的resNet比18层的resNet在训练集和验证集上的误差都要小,说明并没有出现退化现象。34层的resNet与34层的plain网络相比,误差减少了3.5%,说明在深度网络中残差学习是有效的。另外,18层的ResNet与18层的plain网络相比,18层的ResNet训练更快了。
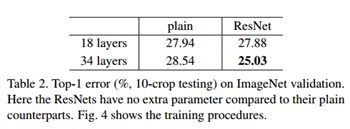
上面展示了,恒等映射(identity shortcuts)可以帮助训练。下面我们测试一下projection shortcuts(公式2)的效果。有3种测试方案。A)当维度增加时,使用zero-padding shortcuts,这些所有的shortcuts是没有参数的(与Table2和Fig4右侧的图一致);B) projection shortcuts只用于维度增加的情况,其他情况(输入输出维度一致时)还是使用恒等映射(即公式1);C)所有的shortcus都是projection(即公式2)。测试结果如下表:
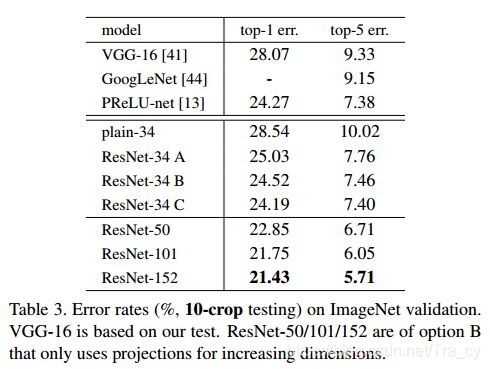
从上表中可以看出,方案A,B和C的效果都要比plain-34要好。B比A稍微好一点,这是因为A的用零填充的那几个维度没有进行残差学习。C要B好的多,这是因为引入了额外的参数。但是总体上A,B和C的差别还是比较小的,说明projection shortcuts在解决退化问题中并不是十分重要。因此,为了减少参数和计算量,我们在这篇文章中不使用方案C。
Deeper Bottleneck Architectures
下面描述用于ImageNet的更深的网络结构。考虑到训练时间,我们将下图中左侧的网络改成右侧的网络。1x1的卷积的作用是减少和增加(恢复)维度,使得3x3的卷积核的个数可以减少。

50-layer ResNet
将34层中的每个2-layer block替换为3-layer bottleneck block,就得到了一个50层的ResNet。我们使用B方案来增加维度。
101-layer and 152-layer ResNets
我们使用更多的3-layer bottleneck block,就得到了101层和152层的ResNet。152层的网络深度很深,但是参数量却比VGG16/19要小。
模型之间的比对
如下图所示,下图中的ResNet是使用多个不同深度的ResNet,综合结果而成的,效果非常好。
