数字图像处理实验之图像灰度变换与空间滤波
数字图像处理_图像灰度变换与空间滤波
- 1. 实验目的
- 2. 实验流程
- 2.1 绘制图像直方图
- 2.2 灰度变换
- 2.3 直方图均衡化
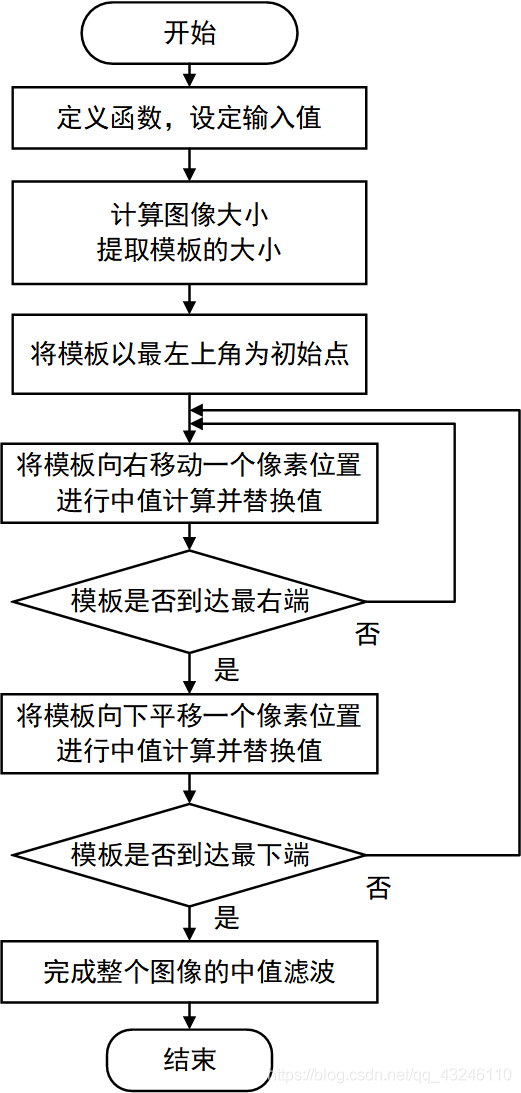
- 2.4 中值滤波
- 2.5 自定义中值滤波函数
- 3. 实验代码
- 3.1 生成并绘制图像直方图
- 3.2 灰度变换
- 3.3 直方图均衡化
- 3.4 中值滤波函数
- 3.5 图像中值滤波
- 4. 实验结果与分析
- 4.1 生成并绘制图像直方图实验分析
- 4.2 灰度变换实验分析
- 4.3 直方图均衡化分析
- 4.4 中值滤波实验分析
1. 实验目的
1.掌握图像直方图的概念和计算方法;
2.理解基于变换函数的图像灰度变换基本原理;
3.理解直方图均衡化的原理;
4.掌握图像空域滤波的基本步骤;
5.熟悉Matlab相关的图像处理操作函数,如imhist函数,imadjust函数,histeq函数,medfilt2函数等。熟悉函数的输入、输出值含义,掌握函数调用和使用。
2. 实验流程
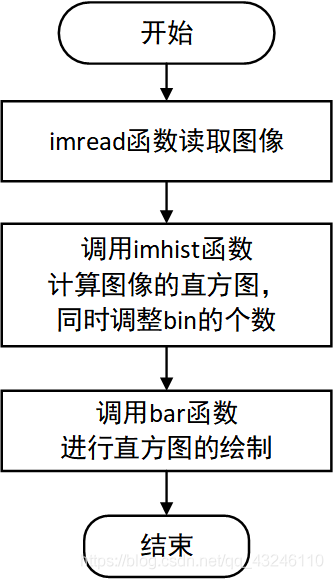
2.1 绘制图像直方图
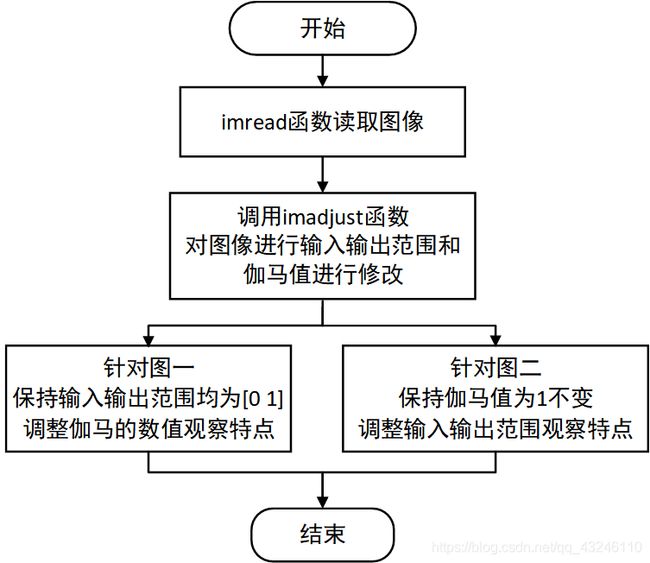
2.2 灰度变换
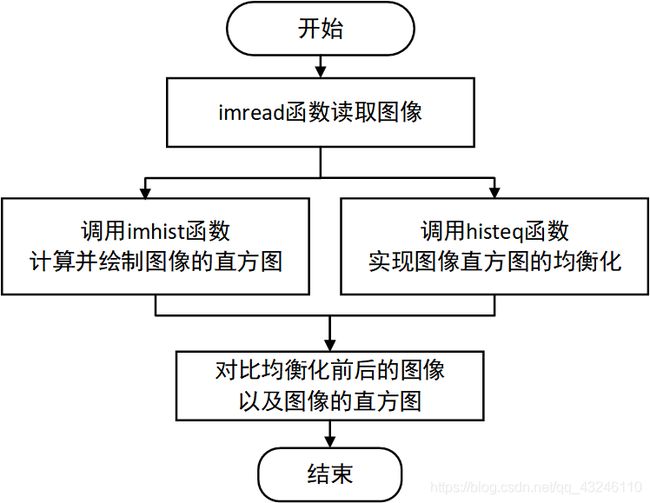
2.3 直方图均衡化
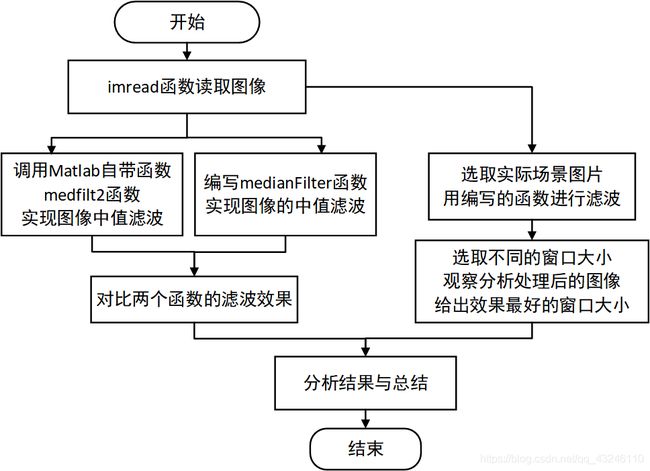
2.4 中值滤波
2.5 自定义中值滤波函数
3. 实验代码
3.1 生成并绘制图像直方图
%% 直方图的绘制函数
% imhist函数的使用,绘制图像的直方图
clear,clc,close ALL;
tic
%计算图像并绘制直方图
I1 = imread('直方图统计实验1.tif');
I2 = imread('直方图统计实验2.tif');
I3 = imread('直方图统计实验3.tif');
I4 = imread('直方图统计实验4.tif');
figure('Name','原图像','NumberTitle','off');
subplot(2,2,1),imshow(I1),title('图一');
subplot(2,2,2),imshow(I2),title('图二');
subplot(2,2,3),imshow(I3),title('图三');
subplot(2,2,4),imshow(I4),title('图四');
%使用bar函数绘制图像直方图
P1 = imhist(I1,64);
P2 = imhist(I2,64);
P3 = imhist(I3,64);
P4 = imhist(I4,64);
figure('Name','图像的直方图绘制','NumberTitle','off');
subplot(2,2,1);horz1 = linspace(0,255,64);
bar(horz1,P1);title('bar函数绘制图一');ylim('auto');
subplot(2,2,2);horz2 = linspace(0,255,64);
bar(horz2,P2);title('bar函数绘制图二');ylim('auto');
subplot(2,2,3);horz3 = linspace(0,255,64);
bar(horz3,P3);title('bar函数绘制图三');ylim('auto');
subplot(2,2,4);horz4 = linspace(0,255,64);
bar(horz4,P4);title('bar函数绘制图四');ylim('auto');
toc
3.2 灰度变换
%% 灰度变换操作函数
% imadjust函数的使用,对灰度级图像进行灰度变换
clear,clc,close ALL;
tic
%第一张图片的灰度变换
P1 = imread('灰度变换实验1.tif');
A1 = imadjust(P1, [0 1], [0 1], 0.2);
A2 = imadjust(P1, [0 1], [0 1], 0.5);
A3 = imadjust(P1, [0 1], [0 1], 1);
A4 = imadjust(P1, [0 1], [0 1], 1.5);
A5 = imadjust(P1, [0 1], [0 1], 2);
figure('Name','第一幅图灰度变换','NumberTitle','off');
subplot(2,3,1);
imshow(P1);title('原图像');
subplot(2,3,2);
imshow(A1);title('gamma值为0.2');
subplot(2,3,3);
imshow(A2);title('gamma值为0.5');
subplot(2,3,4);
imshow(A3);title('gamma值为1');
subplot(2,3,5);
imshow(A4);title('gamma值为1.5');
subplot(2,3,6);
imshow(A5);title('gamma值为2');
%第二张图片的灰度变换
P2 = imread('灰度变换实验2.tif');
B1 = imadjust(P2, [0.25 0.75], [0 1], 1);
B2 = imadjust(P2, [0 1], [0.25 0.75], 1);
B3 = imadjust(P2, [0 1], [1 0], 1);
B4 = imadjust(P2, [0 1], [0 0.5], 1);
B5 = imadjust(P2, [0 1], [0.5 1], 1);
figure('Name','第二幅图原图&灰度变换图','NumberTitle','off');
subplot(2,3,1);
imshow(P2);title('原图像');
subplot(2,3,2);
imshow(B1);title('gamma值为1,[0.25 0.75] → [0 1]');
subplot(2,3,3);
imshow(B2);title('gamma值为1,[0 1] → [0.25 0.75]');
subplot(2,3,4);
imshow(B3);title('gamma值为1,[0 1] → [1 0]');
subplot(2,3,5);
imshow(B4);title('gamma值为1,[0 1] → [0 0.5]');
subplot(2,3,6);
imshow(B5);title('gamma值为1,[0 1] → [0.5 1]');
toc
3.3 直方图均衡化
%% 直方图均衡化函数
% histeq函数的使用,实现直方图的均衡化
clear,clc,close ALL;
tic
%第一张图片
P1 = imread('直方图均衡化1.tif');
figure('Name','第1幅图像','NumberTitle','off');
subplot(2,2,1);
imshow(P1);title('原图像1');
subplot(2,2,3);
imhist(P1);title('原图像1直方图');ylim('auto');
%第一张图片的均衡化
T1 = histeq(P1, 256);
subplot(2,2,2);
imshow(T1);title('均衡化后图像1');
subplot(2,2,4);
imhist(T1);title('均衡化后图像1直方图');ylim('auto');
%第二张图片
P2 = imread('直方图均衡化2.tif');
figure('Name','第2幅图像','NumberTitle','off');
subplot(2,2,1);
imshow(P2);title('原图像2');
subplot(2,2,3);
imhist(P2);title('原图像2直方图');ylim('auto');
%第二张图片的均衡化
T2 = histeq(P2, 256);
subplot(2,2,2);
imshow(T2);title('均衡化后图像2');
subplot(2,2,4);
imhist(T2);title('均衡化后图像2直方图');ylim('auto');
toc
3.4 中值滤波函数
%自定义函数实现中值滤波
function B = medianFilter(A, filter)
[height, width] = size(A);
image_in = uint8(A);
image_out = image_in;
m = filter(1);
n = filter(2);
for i=1:height-m+1
for j=1:width-n+1
c = image_in(i:i+(m-1),j:j+(n-1));
c = c(:);
ans = median(c);
xx = round(i+(m-1)/2);
yy = round(j+(n-1)/2);
image_out(xx,yy) = ans;
end
end
B = image_out;
3.5 图像中值滤波
%% 自定义中值滤波器
clear,clc,close ALL;
tic
%第一张图片
P1 = imread('noiseImg.tif');
P2 = imread('img.tif');
k1 = 5;
F11 = medfilt2(P1,[k1, k1]);
F12 = medianFilter(P1, [k1, k1]);
F21 = medfilt2(P2,[k1, k1]);
F22 = medianFilter(P2, [k1, k1]);
%实验图像测试
figure('Name','中值滤波对比图1','NumberTitle','off');
subplot(2,3,1);imshow(P1);title('原图');
subplot(2,3,2);imshow(F11);title('Matlab自带函数实现');
subplot(2,3,3);imshow(F12);title('自定义函数实现');
subplot(2,3,4);imshow(P2);title('原图');
subplot(2,3,5);imshow(F21);title('Matlab自带函数实现');
subplot(2,3,6);imshow(F22);title('自定义函数实现');
% 实际场景图像演练
P2 = imread('IMG_20181228_004340(1).tif');
k2 = 5;
k3 = 11;
k4 = 15;
F21 = medianFilter(P2,[k2,k2]);
F22 = medianFilter(P2,[k3,k3]);
F23 = medianFilter(P2,[k4,k4]);
figure('Name','实际应用','NumberTitle','off')
subplot(2,2,1);imshow(P2);title('原图');
subplot(2,2,2);imshow(F21);title('k=5');
subplot(2,2,3);imshow(F22);title('k=11');
subplot(2,2,4);imshow(F23);title('k=15');
toc
4. 实验结果与分析
4.1 生成并绘制图像直方图实验分析
1、实验原图:

2、直方图绘制结果:
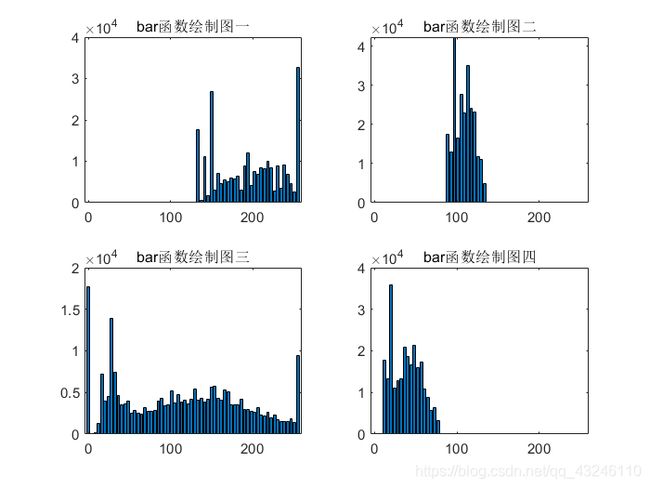
3、结果分析:
针对图3.1中的图一,图像看起来偏白,即亮度偏高。观察图3.2中其对应的直方图,可看出图一的直方图灰度大部分分布在130-250 之间,而在低灰度区域基本无值,因此导致图像整体偏亮;
针对图3.1中的图二,图像看起来很灰暗,有一些模糊的感觉,观察起来不是很舒适。观察图3.2中其对应的直方图,可看出图二的直方图灰度大部分分布在100-140之间,因此导致图像整体没有较大的灰度变化,集中在中间灰度区域,导致图像灰暗。
针对图3.1中的图三,图像看起来比较舒适,黑白分明,整体图像较正常。观察图3.2中其对应的直方图,可看出图三的直方图灰度基本上涵盖了0-255的范围,分布较为均衡,有黑有白,因此使得图像整体让人看起来很舒适自然。
针对图3.1中的图四,图像看起来非常暗,基本看不到内容和细节。观察图3.2中其对应的直方图,可看出图四的直方图灰度基本上只在80以下的范围,导致整个图像很暗,不适合观察。
综合上述分析,可以看出:
①图像直方图直观地反应了图像灰暗程度和灰度分布,并合理地解释了图像呈现效果的原因。
②若一幅图像的像素倾向于占据整个可能的灰度级并且分布均匀,则该图像会有高对比度的外观并展示灰色调的较大变化。最终效果是将一幅灰度细节丰富且动态范围较大的图像。
③直方图均衡化操作使得效果偏暗或偏亮的图像均能实现对比度调整,弥补了图像在视觉上难以区分灰度级的差别,也因此体现出了直方图均衡作为自适应对比度增强工具的强大作用。
4.2 灰度变换实验分析

2、结果分析
本实验中,将两幅原图进行分类研究。针对原图像一,保持其输入输出范围不变,调整其伽马值产生新的图像,从而观察伽马值对图像灰度变换的影响和效果;针对原图像二,保持其伽马值为1不变,通过调整其输入输出范围,从而观察其灰度变换的效果并做合理分析。下面进行详细分析:
(a)第一幅图像
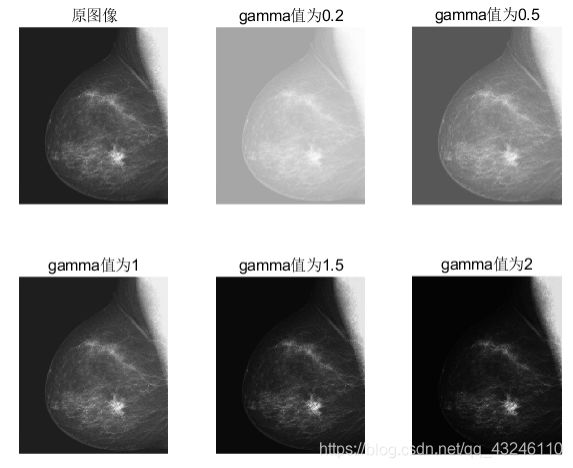
①图3.3中的图一即为第一幅图的原图像。
②图3.3中的图二gamma值为0.2,可以看出其整幅图像偏亮,根据伽马变化原理(如图1.1不同下的伽马变换曲线图),可得输入的灰度级r=L/4的部分基本上以及被拉伸为输出灰度级s=3L/4。
③图3.3中的图三gamma值为0.5,看出其整幅图像也偏亮,但介于原图和gamma值为0.2之间。
④图3.3中的图四gamma值为1,由于输入输出范围也是[0 1]没有变化,也正如观测一致,图四和原图图一相比没有变化。
⑤图3.3中的图五其gamma值为1.5,看出其整幅图像偏暗。
⑥图3.3中的图六其gamma值为2,观察到其整幅图像更暗,与伽马变换曲线相符。
(b)第二幅图像
①图3.4中的图一即为第二幅图的原图像。
②图3.4中的图二gamma值为1,将输入[0.25 0.75]对应输出为[0 1],根据图像可以看出图二的接近0或255的部分更加充足了,图像黑白两端占比更大了,看起来较原图更加清晰可视。
③图3.4中的图三gamma值为1不变,将输入[0 1]对应输出为[0.25 0.75],根据图像可以看出图三的处理效果刚好与图像二的处理效果相反,最黑最白的两部分反而变得较灰了,灰度中间的部分占比较大,整幅图像看起来比原图的对比度更加低了。
④图3.4中的图四gamma值为1不变,将输入[0 1]对应输出为[1 0],根据图像可以看出图四的操作效果为图像的反转,将黑变白将白变黑,产生了负片的效果。
⑤图3.4中的图五gamma值为1不变,将输入[0 1]对应输出为[0 0.5],根据图像可以看出图像整体变暗,失去了像素值大于128的部分。
⑥图3.4中的图六gamma值为1不变,将输入[0 1]对应输出为[0.5 1],根据图像可以看出图像整体变亮,失去了像素值小于128的部分。
©综合上述分析,可以看出:
①灰度变换中的伽马变换在通用的对比度操作中很有用,可以实现图像反转、扩展灰度级和压缩灰度级等作用。
②扩展灰度级时,可将较暗且暗处细节显现不出的图像进行灰度级扩充,使得图像可视化部分和细节进行增强,从而观察到原本观察不到的图像内容。
③压缩灰度级时,可以将现有的图像进行“冲淡”,将过分饱和的图像进行适当压缩,从而输出一个较为直观而可视的图像。
4.3 直方图均衡化分析
1、实验结果
图一:
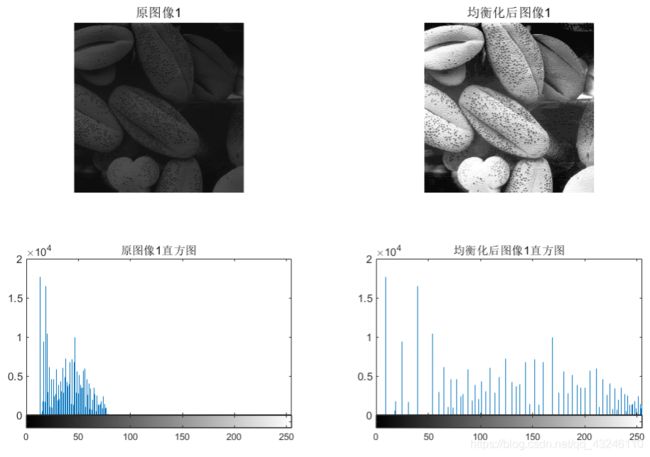
图二:
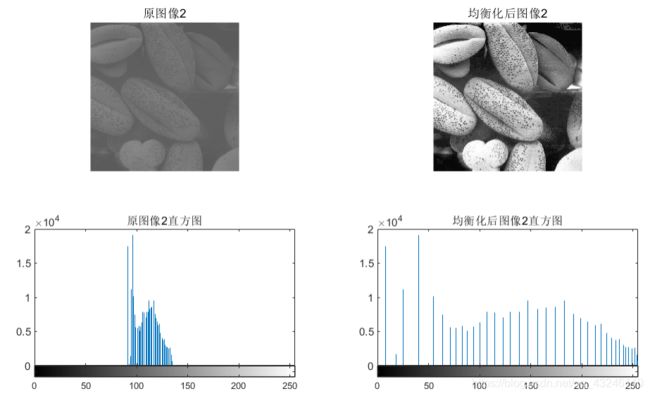
2、结果分析
本实验中,分别对图像1和图像2这两种直方图不均衡的图像进行处理。由图3.5和图3.6观察可知,原图像均为灰度范围单一的图像,其原因即直方图中灰度值集中在一个范围。因此,在对两幅图像对应做了直方图均衡化之后,直方图明显进行了扩展拉伸,使得灰度范围较为均匀地占满了[0 255],其对应的处理后的图像也看起来非常的清晰可观,对比度也有了很好的改善,整体图像处理效果较好。也体现了直方图均衡化的重要意义和应用。
4.4 中值滤波实验分析
1、实验结果
图一:

2、结果分析
由图可得,(a)和(d)分别为两幅图的原图,(b)和(e)为Matlab自带函数对两幅图的处理,而©和(f)是应用自定义函数对原图进行中值滤波处理的图像。
针对第一幅图像的滤波情况,将(b)和©两幅图放大进行观察,发现采用自定义函数medianFilter处理得到的图像和Matlab自带函数medfilt2处理得到的图像一样,但是观察边界部分,发现在图像的边界处,©比(b)更加的精细。探究原因,也正是因为自定义函数medianFilter没有进行边界处理,而medfilt2函数却对边界进行了一定的处理,解释了上述不同的原因。两种中值滤波器都很好地处理了噪声(椒盐噪声)。
针对第二幅图像的滤波情况,将(b)和©两幅图进行对比观察分析,发现两幅图一模一样。探究原因,因为边界处的灰度值处于中间值位置,并没有较暗或较亮。因此边界处并无影响。
综合上述分析,可知:
中值滤波器使用像素邻域内灰度的中值代替该像素的值,其应用非常普遍,对于一定类型的随机噪声,提供了一种优秀的去噪能力,而且比相同尺寸的线性平滑滤波器的模糊程度明显要低。根据中值滤波器的处理特性特点,其处理脉冲噪声(椒盐噪声)非常有效。
(3)课外场景检验:
为验证中值滤波器的实际应用效果,本报告中提供了一张课外图像进行滤波检验,通过调用自定义中值滤波函数进行中值处理,再对滤波器的掩膜大小进行调整、测试,最终给出不同情况下的结果图,从而进一步分析实验结果,具体测试图如下:

由图3.8可知,原图是含有很多“盐”噪声的,原因来自于电脑屏幕上的灰尘。因此中值滤波器处理在原理上满足图像处理需求。由于噪声大小不确定,不能一次性选取好最佳掩膜大小,因此在本报告中进行了不同大小掩膜的测试,分别取k=5,k=11,k=15进行滤波处理。经过对比分析,得到如下结果:取k=5时,很多“盐”噪声并非处理完好,说明掩膜大小还是不够,没有达到很好的滤波效果;取k=11时,“盐”噪声处理的还可以,基本噪声处理掉了,但还是没有处理的很完善;取k=15时,“盐”噪声全部处理完成,处理效果较好,几乎看不到图像中电脑上的灰尘,显示了中值滤波的实际应用。同时,本报告的拓展也体现了数字图像处理应用的试错性特点以及探索性精神。