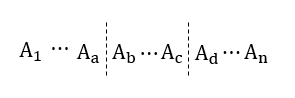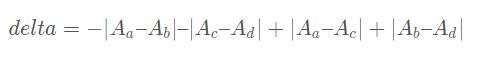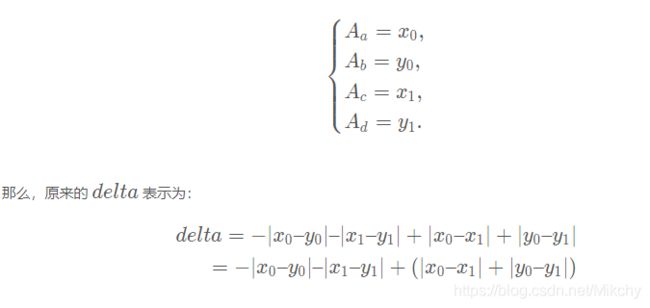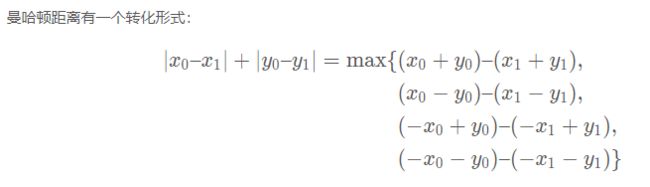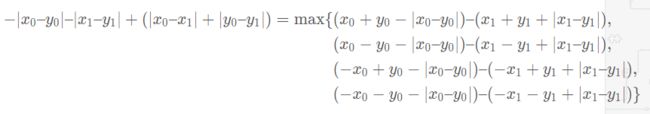LeetCode第18场双周赛（Biweekly Contest 18）解题报告

大年初一的双周赛，没啥人参加，虽然做了三题，159名，但是总人数少，感觉又是掉分的一周，哭泣泣。

第一题：模拟。

第二题：模拟。

第三题：模拟。

第四题：最大曼哈顿距离。

详细题解如下。

---

1. 数组序号转换（Rank Transform of An Array）

           AC代码（C++）

2. 破坏回文串（Break A Palindrome）

           AC代码（C++）

3.将矩阵按对角线排序（Sort The Matrix Diagonally）

           AC代码（C++）

4.翻转子数组得到最大的数组值（Reverse Subarray to Maximize Array Value）

           AC代码（C++）

---

LeetCode第18场双周赛地址：

https://leetcode-cn.com/contest/biweekly-contest-18/

---

1. 数组序号转换（Rank Transform of An Array）

题目链接

https://leetcode-cn.com/problems/rank-transform-of-an-array/

题意

给你一个整数数组 arr ，请你将数组中的每个元素替换为它们排序后的序号。

序号代表了一个元素有多大。序号编号的规则如下：

• 序号从 1 开始编号。
• 一个元素越大，那么序号越大。如果两个元素相等，那么它们的序号相同。
• 每个数字的序号都应该尽可能地小。

示例 1：

输入：arr = [40,10,20,30]
输出：[4,1,2,3]
解释：40 是最大的元素。 10 是最小的元素。 20 是第二小的数字。 30 是第三小的数字。

提示：

• 0 <= arr.length <= 105
• -109 <= arr[i] <= 109

解题思路

题目很简单，题目的要求，我们要将数组中的元素，替换成对应的排序后的序号。

因此，我们将数组复制，进行排序（因为要排序，原本数组的顺序不能变动，所以复制对应的数组）。

接着，我们为了可以方便的查询，对应某个数的排序序号，我们利用map，将<数值，序号>进行存储。

最后，遍历原本的额数组，将对应的数值，利用 map 得到对应的序号后，进行替换。

 

AC代码（C++）

class Solution {
public:
    vector arrayRankTransform(vector& arr) {
        vector temp = arr;
        
        sort(temp.begin(), temp.end());
        
        unordered_map mp;
        int cnt = 1;
        for(int i = 0;i < temp.size(); ++i)
        {
            if(mp[temp[i]] == 0)
            {
                mp[temp[i]] = cnt++;
            }
        }
        for(int i = 0;i < arr.size();i++)
        {
            arr[i] = mp[arr[i]];
        }
        return arr;
    }
};

 

---

2. 破坏回文串（Break A Palindrome）

题目链接

https://leetcode-cn.com/problems/break-a-palindrome/

题意

给你一个回文字符串 palindrome ，请你将其中 一个 字符用任意小写英文字母替换，使得结果字符串的字典序最小，且 不是 回文串。

请你返回结果字符串。如果无法做到，则返回一个空串。

示例 1：

输入：palindrome = "abccba"
输出："aaccba"

示例 2：

输入：palindrome = "a"
输出：""

提示：

• 1 <= palindrome.length <= 1000
• palindrome 只包含小写英文字母。

解题思路

根据题目意思，我们要将一个字符串改变一个字符，同时要破坏字符串，不是回文串。

那么当，字符串本身是空串或者长度为1的时候，无论我们怎么操作，是破坏不了回文串，因此此时的结果一定是空串。

那么接下来，为了要使得字符串字典序最小，那么我们就是从前遍历，当需要不是 ‘a’ 的时候，说明这个字符可以变动，那我们就变为 ’a‘，使得字典序比原本的小。当改变的时候，我们要检查，改变之后还是不是回文串，如果是回文串，那么改变这个位置是没有用的，那么就要判断下一个位置。

最后，当我们遍历完之后，再次检查，还是不是回文串

如果不是回文串，说明我们已经处理过了，可以直接返回结果

如果还是回文串，说明前面没有处理，那就是说明前面无法处理，有点类似于 "aaa"，那么我们要使得改变后的字符串的字典序最小，我们就将最后一个字符改为 b 即可。

 

AC代码（C++）

class Solution {
public:
    
    bool ishui(string p)
    {
        int n = p.size();
        for(int i = 0;i < n/2; ++i)
        {
            if(p[i] != p[n - 1 - i])
                return false;
        }
        return true;
    }
    
    string breakPalindrome(string p) {
        int n = p.size();
        if(n==1 || n==0) return "";
        
        string temp = p;
        for(int i = 0;i < n; ++i)
        {
            if(temp[i] != 'a')
            {
                temp[i] = 'a';
                if(!ishui(temp))
                    break;
                else
                    temp = p;
            }
        }
        if(!ishui(temp)) return temp;
        temp[n - 1] = 'b';
        return temp;
   
    }
};

 

---

3.将矩阵按对角线排序（Sort The Matrix Diagonally）

题目链接

https://leetcode-cn.com/problems/sort-the-matrix-diagonally/

题意

给你一个 m * n 的整数矩阵 mat ，请你将同一条对角线上的元素（从左上到右下）按升序排序后，返回排好序的矩阵。

示例 1：

（示例有图，具体看链接）

输入：mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
输出：[[1,1,1,1],[1,2,2,2],[1,2,3,3]]

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 100
• 1 <= mat[i][j] <= 100

解题分析

根据题目的数据范围，我们可以直接按照题意进行模拟即可。

也就是，我们遍历所有对角线的起点（即第一行，和，第一列），然后将该起点对应的对角线上的元素保存在一个数组中，接着对该数组进行排序，接着将排序好的数，按照位置又一个个放回对角线上。

那么时间复杂的应该大概是 O(n * (n + n*logn + n) )。不会超时。 

 

AC代码（C++）

class Solution {
public:
    vector> diagonalSort(vector>& mat) {
        int n = mat.size(), m = mat[0].size();
        vector nums;
        nums.clear();
        // 第一行的所有列
        for(int j = m - 1; j >= 0; --j)
        {
            int x = 0, y = j;
            while(x < n && y < m) // 对应对角线上所有元素
            {
                nums.push_back(mat[x][y]);
                x++, y++;
            }
            sort(nums.begin(), nums.end());
            
            x = 0, y = j;
            int cnt = 0;
            while(x < n && y < m)
            {
                mat[x][y] = nums[cnt++];
                x++, y++;
            }
            nums.clear();  
        }
        // 第一列的所有行
        for(int i = 1; i < n; ++i)
        {
            int x = i, y = 0;
            while(x < n && y < m)
            {
                nums.push_back(mat[x][y]);
                x++, y++;
            }
            sort(nums.begin(), nums.end());
            
            x = i, y = 0;
            int cnt = 0;
            while(x < n && y < m)
            {
                mat[x][y] = nums[cnt++];
                x++, y++;
            }
            nums.clear();  
        }
    
        return mat;
    }
};

 

---

4.翻转子数组得到最大的数组值（Reverse Subarray to Maximize Array Value）

题目链接

https://leetcode-cn.com/problems/reverse-subarray-to-maximize-array-value/

题意

给你一个整数数组 nums 。「 数组值」定义为所有满足 0 <= i < nums.length-1 的 |nums[i]-nums[i+1]| 的和。

你可以选择给定数组的任意子数组，并将该子数组翻转。但你只能执行这个操作 一次 。

请你找到可行的最大 数组值 。

示例 1：

输入：nums = [2,3,1,5,4]
输出：10
解释：通过翻转子数组 [3,1,5] ，数组变成 [2,5,1,3,4] ，数组值为 10 。

示例 2：

输入：nums = [2,4,9,24,2,1,10]
输出：68

提示：

• 1 <= nums.length <= 3*10^4
• -10^5 <= nums[i] <= 10^5

解题分析

一开始，想到使用双指针，暴力枚举所有的可能翻转情况，然后求出其中的最大值，时间复杂度就是 O(N ^ 2)。根据题目的数据范围，会超时，然后GG，我是没做出来，最后看了一个题解，理解了思路之后，才知道如何做。

参考了题解链接：LeetCode 5154. 翻转子数组得到最大的数组值

 

首先，对示例 1 进行一个题目分析，从而进一步理解题目

2,3,1,5,4  -> 数组值：1 + 2 + 4 + 1 = 8
翻转 [3 1 5] 之后
2,5,1,3,4  -> 数组值：3 + 4 + 2 + 1 = 10

我们可以发现，当我们翻转子数组后，子数组内部的数组值，是不会发生变化的，主要的变化，是两个端点的数组值。

对于一般的数组，翻转区间操作仅与边界处的四个数字有关系。因为目标式是相邻两个元素差值之和，翻转操作仅改变边界四个数字的相邻关系，其他都不改变。

假设，不翻转时目标式的值为 sum，我们其实是要求一个 ，其中 delta 时翻转操作对于答案的改变。

上面这段话，是关键，对于交叉项，我们需要 O(N ^ 2)，但是这样子会超时，所以要处理，怎么有效的求解出 delta，即降低时间复杂度。

交叉项的形式其实是一个曼哈顿距离的形式

对于上面的转化形式，证明可以看：【算法，数学知识】曼哈顿距离

因此，将等式带入delta的表达式中，可以的得到

因此我们分成四种情况求，每一种情况 A-B，求出A的最大值，B的最小值，从而得到这种情况的A-B的最大值，取四种情况中的最大值。这样子时间复杂度就是O(N)级别的。

 

这道题，还有三个特殊情况：

1）没有翻转，那就是原本的sum

2）翻转的时候，左端点是数组的第一个值，这样子改变的数组值，只有右端点会变，遍历取最大值O(N)

3）同样的，翻转的时候，右端点是数组最后一个值，这样子改变的额数组值，只有左端点会变，遍历取最大值O(N)

 

因此，相当于总共有，7中情况，取出里面的最大值，即可。

 

AC代码（C++）

#define INF 1e6 + 50

class Solution {
public:
    int maxValueAfterReverse(vector& nums) {
        int sum = 0;
        int n = nums.size();
        for(int i = 0;i < n - 1; ++i)
            sum += abs(nums[i] - nums[i + 1]);

        int ans = sum;

        // 翻转数组左端点是第一个值，所以只改变右端点的数值值
        for(int i = 1;i < n - 1; ++i)
            ans = max(ans, sum + abs(nums[0] - nums[i + 1]) - abs(nums[i] - nums[i + 1]));

        // 翻转数组右端点是最后一个值，所以只改变左端点的数值值
        for(int i = n - 2; i >= 1; --i)
            ans = max(ans, sum + abs(nums[n-1] - nums[i - 1]) - abs(nums[i] - nums[i - 1]));
        
        // 四种情况的第一种，分别先求出 A-B，A的最大值和B的最小值
        int mx = -INF, mn = INF;
        for(int i = 0;i < n - 1; ++i)
        {
            mx = max(mx, nums[i] + nums[i + 1] - abs(nums[i] - nums[i + 1]));
            mn = min(mn, nums[i] + nums[i + 1] + abs(nums[i] - nums[i + 1]));
        }
        ans = max(ans, sum + mx - mn);
        
        // 第二种情况
        mx = -INF, mn = INF;
        for(int i = 0;i < n - 1; ++i)
        {
            mx = max(mx, -nums[i] - nums[i + 1] - abs(nums[i] - nums[i + 1]));
            mn = min(mn, -nums[i] - nums[i + 1] + abs(nums[i] - nums[i + 1]));
        }
        ans = max(ans, sum + mx - mn);

        // 第三种情况
        mx = -INF, mn = INF;
        for(int i = 0;i < n - 1; ++i)
        {
            mx = max(mx, nums[i] - nums[i + 1] - abs(nums[i] - nums[i + 1]));
            mn = min(mn, nums[i] - nums[i + 1] + abs(nums[i] - nums[i + 1]));
        }
        ans = max(ans, sum + mx - mn);

        // 第四种情况
        mx = -INF, mn = INF;
        for(int i = 0;i < n - 1; ++i)
        {
            mx = max(mx, -nums[i] + nums[i + 1] - abs(nums[i] - nums[i + 1]));
            mn = min(mn, -nums[i] + nums[i + 1] + abs(nums[i] - nums[i + 1]));
        }
        ans = max(ans, sum + mx - mn);

        return ans;
    }
};