【论文笔记】Bayesian Loss for Crowd Count Estimation with Point Supervision

Abstract

在人群计数数据集中，每个人都被一个点标注，这个点通常是头部的中心。任务是估计一个人群场景中的总人数。目前最先进的方法大多基于密度图估计，将稀疏点标注通过Gaussian kernel转换为“ground truth”密度图，然后将其作为学习目标来训练密度图估计器。然而，由于遮挡、透视效果、物体形状的变化等原因，这种“ground truth”密度图并不完美。相反，我们提出了一种新的损失函数——Bayesian loss，它从点注释的角度构造了一个密度贡献概率模型。提出的训练损失不是对密度图中每个像素的值进行约束，而是对每个注释点的计数期望进行更可靠的监督。如果没有附加的功能，损失函数将大大改善所有测试数据集的baseline loss。此外，我们的loss配备了一个标准的主干网络，不使用任何外部探测器或多尺度架构，对目前的技术状态起到了积极的作用。在最新和最大的UCF-QNRF数据集上，我们的方法大大优于以前的最佳方法。源代码可以在https://github.com/ZhihengCV/Bayesian-Crowd-Counting找到。
数据集参考：https://blog.csdn.net/NcepuKZH/article/details/89349623

1.Introduction

利用计算机视觉技术对密集人群进行计数是近年来备受关注的研究课题。它有广泛的应用，如估计规模，并计算参加政治集会，民间动乱，社会和体育活动的人数等。此外,人群计数的方法也有很大的潜力来处理类似的任务在其他领域,包括估计交通拥堵的车辆数量、计算细胞和细菌从微观图像、和动物的人群估计生态调查等等。

人群计数是一项非常具有挑战性的任务，因为：1. 密集人群之间往往存在严重的重叠和遮挡；2. 透视效果可能会导致图像中人类的大小、形状和外观发生很大的变化。在过去的十年中，文献中提出了许多人群计数算法。近年来，利用卷积神经网络(Convolutional Neural Networks, CNNs)进行人群计数的方法取得了显著的进展。最好的方法大多基于密度图估计，通常通过预测输入图像的密度图，然后对估计的密度图求和来获得人群计数。目前，用于训练的公开数据集仅为每个训练图像提供点注释，即每个人只有一个像素被标记(通常是头部的中心)。目前，使用这些标注最常见的方法是，首先使用高斯核将每个训练图像的点标注转换为“groundtruth”密度图，然后通过对密度图中每个像素的值进行回归来训练CNN模型。在这种像素级的严格监督下，CNN模型的准确性高度依赖于获得的“groundtruth”密度图的质量。

显然，由于遮挡、不规则的人群分布、物体大小、形状、密度等方面的巨大变化，将假设的高斯核应用于点注释得到的“groundtruth”密度图很难达到高质量。与此相反，我们提出了贝叶斯损失，它从点注释的角度构造了一个密度贡献概率模型。然后，通过对贡献概率和每个像素的估计密度的乘积求和，计算出每个注释点的期望计数。与之前限制每个像素密度值的损失函数相比，我们提出的训练损失对每个注释点的计数期望进行监督。

大量的实验评估表明，在UCF- qnrf[16]、ShanghaiTech[57]和UCF CC 50[15]基准数据集上，所提出的损失函数显著优于基线训练损失。此外，我们提出的损耗函数以标准VGG-19网络[39]为骨干，不使用任何外部探测器或多尺度架构，实现了所有基准数据集的最新性能，特别是与其他方法相比，UCF-QNRF数据集有了显著的改进。

2. Related Work

我们从以下几个方面对文献中关于人群计数估计的相关工作进行了综述。Detection-then-counting. Direct count regression. Density map estimation. Hybrid training.

3. The Proposed Method

3.1. Background and Motivation

$\{D(x_m)>=0:m=1,2,......,M\}$表示一个密度图，其中，$x_m$表示一个二维像素位置，$M$是密度图中的像素总数。

$\{(z_n,y_n):n=1,2,......,N\}$表示样本图像的点注释图，其中N为总人数，$z_n$为顶点位置，$y_n=n$为对应的标签。点注释映射为每个人只包含一个像素(通常是头部的中心)，它是稀疏的，不包含关于对象大小和形状的信息。直接使用这样的点注释图来训练密度映射估计器是很困难的。解决这个问题的一个常用方法是使用高斯核将其转换为“ground truth”密度图。

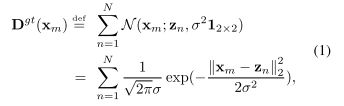
上述公式为正态分布的公式。

为在$x_m$处的2D Gaussian distribution。
最近的工作大多数使用了上面的“ground truth”密度图为学习目标，利用以下损失函数训练一个密度map估计器:

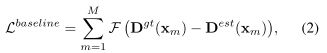
其中$F(\cdot )$为距离函数，$D^{est}$为估计密度图。假设数据集中所有的人都有同样的头部大小和形状，则可以Gaussian kernel 设置为一个固定大小，显然这和实际情况是不符的；另一种解决方案是为每一个n设置一种自适应Gaussian kernel:${\sigma }_n$∝$d_n$, $d_n$是一个距离，取决于其所在空间域的最近邻点，它假定人群是均匀分布的。其他还有一些利用特定的信息的方法，如相机参数，以获得更准确的透视图，但通常这些信息是不可用的。

我们认为，在可用的人群计数数据集中的点注释可以被认为是密度图估计的弱标签。更合理的做法是将这些注释作为先验，而不是学习目标。在训练CNN模型时，采用密度图上Eq.(2)这样严格的像素对像素的监督的损失函数并不总是有利于提高计数估计的准确性，因为它迫使模型学习不准确的，甚至错误的信息。

3.2. Bayesian Loss

设$x$为表示空间位置的随机变量，$y$为表示标注的点的随机变量。在以上讨论的基础上，我们不以Eq.(1)生成的“ground truth”密度图作为学习目标，而是根据所给的标签$y_n$提出构建$x_m$的似然函数.

为了简化符号，我们在下列公式中省略了随机变量x和y，例如，式(3)变成$p(x_m|y_n)=N(x_m;z_n,{\sigma }^2{1}_{2\times 2})$。根据贝叶斯定理，给定密度图中的像素位置$x_m$, $x_m$具有$y_n$标签的后验概率可计算为：

在上面的推导中，第三个等式成立，因为我们假设每个类别标签$y_n$的先验概率相等，即$p(y_n)$ 相等，如$p(y_n)=1/N$。在实践中，如果我们事先知道人群或多或少会出现在某些地方，可以在这里应用一个定制的$p(y_n)$。

利用后验标记概率$p(y_n|x_m)$和估计密度图$D^{est}$，我们得出Bayesian loss如下：令$c_n^m$表示$x_m$贡献$y_n$的count，$c_n$为与$y_n$相关的总count，则$c_n$的期望为：

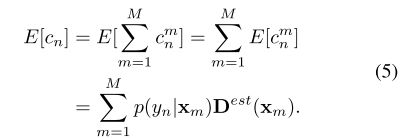
显然，每个注释点的ground-truth count $c_n$为1，因此我们有以下损失函数：

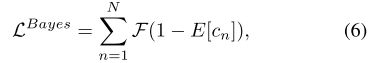
$F(\cdot )$是一个距离函数，在我们的实验中采用 ℓ1 距离表示。当训练图像中没有object时，应处理特殊情况。在这种情况下，我们直接将密度映射的总和强制为零。我们提出的损失函数是可微的，可以很容易地应用到一个给定的CNN使用标准的反向传播训练算法。

在推理阶段，我们不需要提前知道后验标概率$p(y_n|x_m)$，因为当我们对估计的密度图求和时，我们消除了$p(y_n|x_m)$如下：

3.3. Background Pixel Modelling

对于没有任何注释的背景像素，将它们分配给$y_n$没有任何意义。为了更好地建模背景像素，除了标签$\{y_n=n:n=1,2，\dots N\}$,我们引入了一个额外的背景标签$y_0=0$。那么，后验标签概率可以改写为：

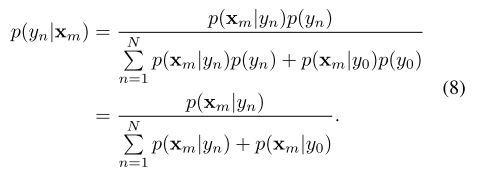
假设$p(y_n)=p(y_0)=\frac{1}{N+1}$，则可以得到最后一个等式。同理，我们有：

人和整个背景的期望count被定义为：

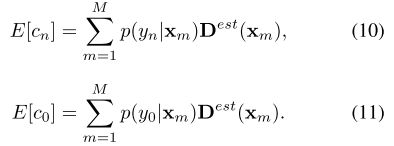
在这种情况下，整个密度图的总和${\sum }_{m=1}^M{D}^{est}(x_m)$包括了foreground counts ${\sum }_{n=1}^{N}E[c_n]$和background count $E[c_0]$。显然，我们希望background count的概率为0，foreground counts的概率为1，因此，我们有以下增强的损失函数。

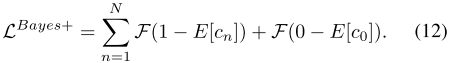
为了定义背景似然，我们为每个像素构造一个虚拟的背景点

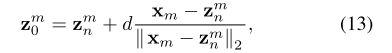
这里的$z_n^m$表示$x_m$最近的注释点，$d$是一个参数，控制head和虚拟背景点之间的空白，如图1所示。使用定义的虚拟背景点$z_0^m$，对于远离head points的像素$x_m$，可以将其分配给背景标签。这里我们也使用Gaussian kerne来定义背景似然。

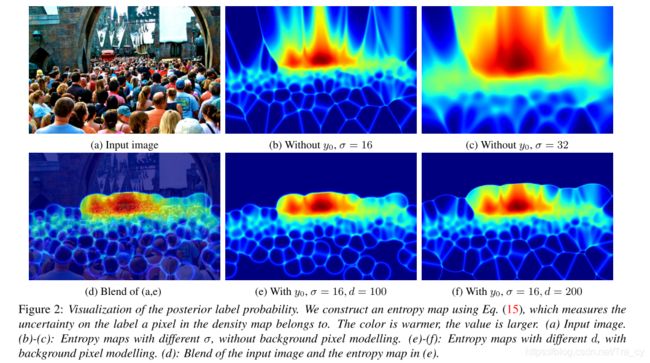
3.4. Visualization and Analysis

我们构建了用于可视化和分析的标签分配的熵映射Ent，它对每个像素$x_m$的计算如下:

熵度量了密度图中像素$x_m$所属的标签上的不确定性。我们在图2中显示了不同设置下的熵图，总结如下：

• 后验可以大致找到人与人之间的界限。
• 密集区域的熵值高于稀疏区域。
• 参数σ控制后softness标签概率,比较(b)和©。
• 对比(b)和(e)，通过背景像素建模，远离人群的像素处理得更好。
• 比较(e)和(f)，参数d控制前景和背景之间的距离。
  

4. Experiments

4.1. Evaluation Metrics

人群计数估计方法采用两种广泛使用的度量标准：平均绝对误差(MAE)和平均平方误差(MSE)，其定义如下：

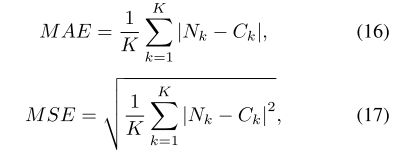
其中K为测试图像的数量，$N_k$和$C_k$分别为第K张图像的ground-truth count和estimated count。

4.2. Datasets

实验评估使用四种广泛使用的人群计数基准数据集：UCFQNRF、UCF CC 50、ShanghaiTech part A和part b。

4.3. Implementation Details

**Network structure.**我们使用标准的图像分类网络，去掉最后的池化层和随后的全连接层。在我们的实验中，我们测试了两个网络:VGG-19和AlexNet。通过双线性插值，我们upsample，网络的输出变为输入图片尺寸的1/8，然后通过一个regression header，它由两个分别为256和128channels的3×3卷积层构成，再通过一个1×1卷积层得到密度图。regression header由MSRA初始化器初始化，网络在ImageNet上预先训练。初始学习速率为$10^{-5}$的Adam优化器用于更新参数。


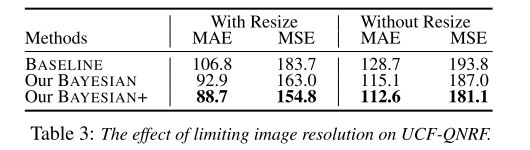
**Training details.**我们使用随机裁剪和水平翻转来增加训练数据。我们注意到UCF-QNRF的图像分辨率从0.08万像素到6600万像素差别很大。然而，常规的CNN由于接受域有限，无法处理各种尺度的图像。因此，在UCF-QNRF中，我们将每个图像的短边限制在2048像素内。然后随机裁剪图像进行训练，图像分辨率较小的ShanghaiTechA和UCF_CC_50的裁剪尺寸为256×256，ShanghaiTechB和UCFQNRF的裁剪尺寸为512×512。在等式(3)和(14)中，我们设置了高斯参数σ为8，式(13)中的距离参数d到图像较短一侧的15%。这些参数是在UCF-QNRF的验证集(从训练集随机抽取的120幅图像)上选择的。

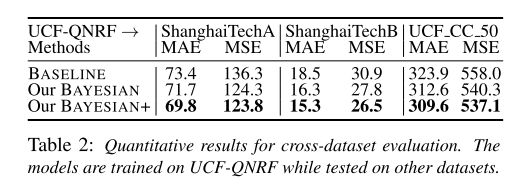
4.4. Experimental Evaluations

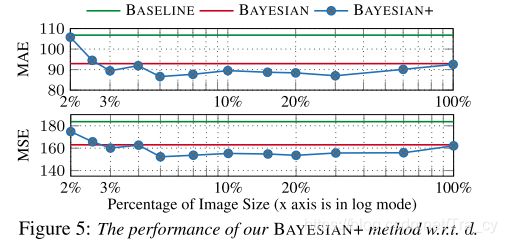
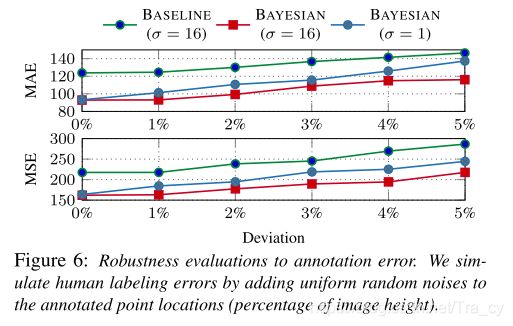
4.5. Ablation Studies

5. Conclusions and Future Work

本文提出了一种新的基于点监督的人群计数估计损失函数。与以往的基于像素监督的Gaussian kernel 将点注释转换为“ground truth”密度图的方法不同，我们的损失函数对每个注释点的计数期望采用了更可靠的监督。大量的实验证明了我们提出的方法在准确性、鲁棒性和泛化方面的优势。我们的公式目前的形式是相当普遍的，可以很容易地结合其他知识，例如，具体的foreground 或background先验，规模和时间的可能性，和其他事实，以进一步完善提出的方法。