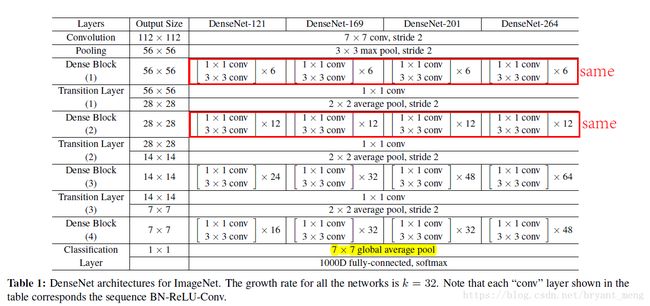
【DenseNet】《Densely Connected Convolutional Networks》
CVPR-2017 best paper award
在 CIFAR-10 上的小实验可以参考博客【Keras-DenseNet】CIFAR-10
文章目录
- 1 Motivation
- 2 Advantages
- 3 Architecture
- 3.1 Dense connectivity
- 3.2 Composite function
- 3.3 Pooling layers
- 3.4 Growth rate
- 3.5 Bottleneck layers(Dense blocks内)
- 3.6 Compression(Dense blocks之间)
- 4 Experiment
- 4.1 Classification Results on CIFAR and SVHN
- 4.2 Classification Results on ImageNet
- 5 Feature Reuse
- 6 作者解读
1 Motivation
As CNNs become increasingly deep, a new research problem emerges: as information about the input or gradient passes through many layers, it can vanish and “wash out” by the time it reaches the end (or beginning) of the network.
目前的解决方法如ResNets、Highway Networks、Stochastic depth等,they all share a key characteristic: they create short paths from early layers to later layers.
作者 distills this insight into a simple connectivity pattern:
each layer obtains additional inputs from all preceding layers and passes on its own feature-maps to all subsequent layers.
在传统的卷积神经网络 L L L层,有 L L L个连接,DenseNet中则会有 L ( L + 1 ) / 2 L(L+1)/2 L(L+1)/2个连接
2 Advantages
DenseNets have several compelling advantages:
- alleviate the vanishing-gradient problem
- strengthen feature propagation
- encourage feature reuse
- substantially reduce the number of parameters
Each layer has direct access to the gradients from the loss function and the original input signal, leading to an implicit deep supervision.
Further, we also observe that dense connections have a regularizing effect, which reduces overfitting on tasks with smaller training set sizes.
3 Architecture
3.1 Dense connectivity
x l = H l ( x l − 1 ) + x l − 1 x_{l} = H_{l}(x_{l-1})+x_{l-1} xl=Hl(xl−1)+xl−1
DenseNet:(Dense blocks)
首先明确,dense connectivity 仅仅是在一个dense block里的,不同dense block 之间是没有dense connectivity 的!
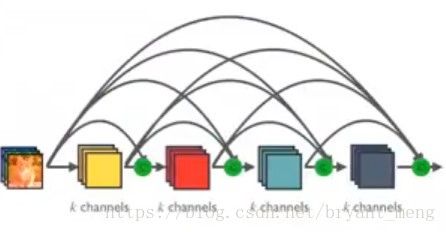
x l = H l ( [ x 0 , x 01 , . . . , x l − 1 ] ) x_{l} = H_{l}([x_{0},x_{01},...,x_{l-1}]) xl=Hl([x0,x01,...,xl−1])
H l ( ⋅ ) H_{l}(·) Hl(⋅) 可以是 BN , ReLU, Pooling, or Convolution
x l x_{l} xl 表示为 the output of the l t h l^{th} lth layer
[ x 0 , x 01 , . . . , x l − 1 ] [x_{0},x_{01},...,x_{l-1}] [x0,x01,...,xl−1]表示 concatenation
Note:
ResNet 的skip-connection 是 addition,eg:11+22 = 33
DenseNet 的skip-connetion是concatenate,eg:11+22 = 1122
3.2 Composite function
we define H l ( ⋅ ) H_{l}(·) Hl(⋅) as a composite function of three consecutive operations:
BN→ReLU→3×3Conv
原版的DenseNet,区别于后面的Bottleneck layers,也即是DenseNet-B
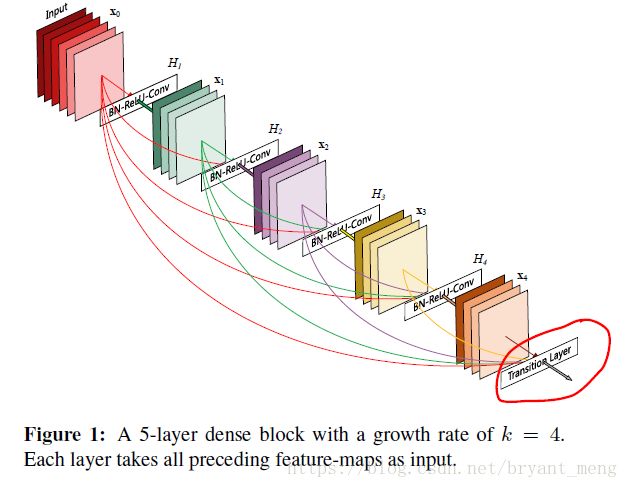
也就是figure 1 中的H1 H2 H3 H4,feature maps大小不会改变
3.3 Pooling layers
Dense blocks 不会改变feature maps 的尺寸,这样网络一直以一个分辨率(w×h)传下去肯定不行,pooling(down-sample)是很有必要的,所以作者把网络分成很多个Dense blocks,Dense blocks 之间的transition layers来做 pooling.
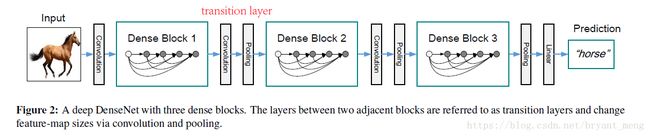
transition layers:在Dense blocks之间,do convolution and pooling:
BN→1×1Conv→2×2 average pooling
3.4 Growth rate
If each function H l H_{l} Hl produces k k k feature maps, it follows that the l t h l^{th} lth layer has k 0 + k × ( l − 1 ) k_{0}+k×(l-1) k0+k×(l−1)input feature-maps, where k 0 k_{0} k0 is the number of channels in the input layer.
Growth rate is k
eg: figure 1 中 x1、x2、x3、x4 k为4
3.5 Bottleneck layers(Dense blocks内)
为了减少feature maps的channels,因为哪怕k很小,层数多了,concatenate起来,feature maps的channels也会很大
BN→ReLU→1×1Conv→BN→ReLU→3×3Conv
这种version of H l ( ⋅ ) H_{l}(·) Hl(⋅) 叫 DenseNet-B
3.6 Compression(Dense blocks之间)
If a dense block contains m m m feature-maps, we let the following transition layer generate [ θ m ] [\theta m] [θm] output feature maps, 0 < θ ≤ 1 0< \theta ≤1 0<θ≤1.
当 θ = 1 \theta =1 θ=1 时,就和原来的transition layer 一样
当 θ < 1 \theta <1 θ<1 时,叫 DenseNet-C
When both the bottleneck and transition layers with θ < 1 \theta <1 θ<1 are used, we refer to our model as DenseNet-BC.
4 Experiment
主要实验都是在三大数据库上进行的,CIFAR、SVHN、ImageNet
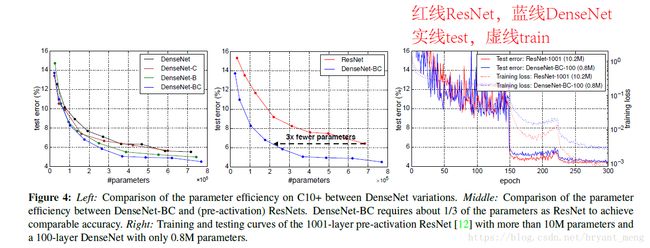
4.1 Classification Results on CIFAR and SVHN
说明以下特点
- Accuracy
- Capacity:L(深度)和k(growth rate)增加,效果变好的general trend
- Parameter Efficiency:参数少,效果好
- Overfitting: DenseNet-BC缓解
4.2 Classification Results on ImageNet
Accuracy:compare with ResNet
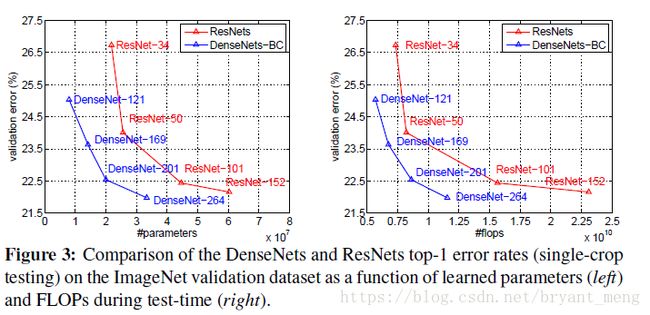
Parameter Efficiency:compare with ResNet
5 Feature Reuse
作者让网络中的每一层都直接与其前面层相连,实现特征的重复利用;同时把网络的每一层设计得特别「窄」,即只学习非常少的特征图(最极端情况就是每一层只学习一个特征图),达到降低冗余性的目的。
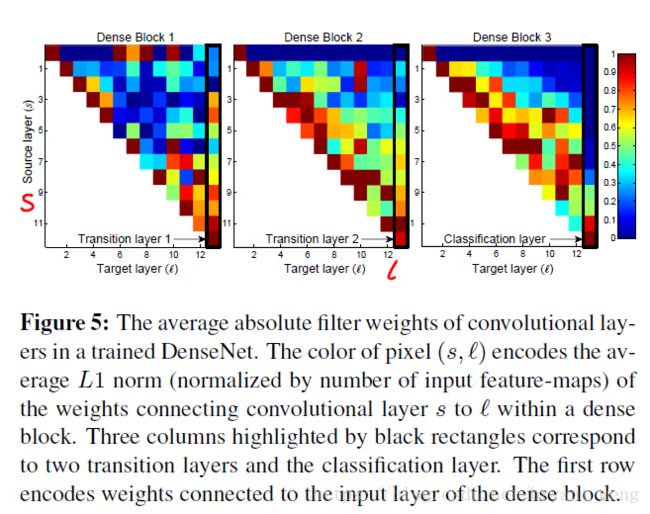
上图可以简单的理解为,分子 l l l 到 s s s 的权重,分母为所有的权重(权重都是用L1范式计算的)
Dense Block2 和 Dense Block3 第一行的值是tansition layer 到下一个Dense block各层的权重,值比较低,说明特征冗余了,所以权重占比比较小!
This is in keeping with the strong results of DenseNet-BC where exactly these outputs are compressed
6 作者解读
CVPR 2017最佳论文作者解读:DenseNet 的“what”、“why”和“how”|CVPR 2017
- DenseNet 是受什么启发提出来的?
很大程度上源于《Deep networks with stochastic depth》
1)神经网络并不一定要是一个递进层级结构,也即网络中的某一层可以不仅仅依赖于紧邻的上一层的特征,而可以依赖于更前面层学习的特征
2)训练的过程中随机扔掉很多层也不会破坏算法的收敛,说明了 ResNet 具有比较明显的冗余性
- 密集连接不会带来冗余吗?
DenseNet 的每一层只需学习很少的特征(特征重用),使得参数量和计算量显著减少
- DenseNet 特别耗费显存?
这个问题其实是算法实现不优带来的(对于大多数框架(如 Torch 和 TensorFlow),每次拼接操作都会开辟新的内存来保存拼接后的特征)
- 使用 DenseNet 有什么需要注意的细节?(供参考)
1)每层开始的瓶颈层(1x1 卷积)对于减少参数量和计算量非常有用。
2)像 VGG 和 ResNet 那样每做一次下采样(down-sampling)之后都把层宽度(growth rate) 增加一倍,可以提高 DenseNet 的计算效率(FLOPS efficiency)
3)与其他网络一样,DenseNet 的深度和宽度应该均衡的变化,当然 DenseNet 每层的宽度要远小于其他模型。
4)每一层设计得较窄会降低 DenseNet 在 GPU 上的运算效率,但可能会提高在 CPU 上的运算效率。
参考
【1】DenseNet算法详解 by AI之路
【2】论文笔记:Densely Connected Convolutional Networks(DenseNet模型详解)
【3】《Densely Connected Convolutional Networks》
【4】CVPR 2017最佳论文作者解读:DenseNet 的“what”、“why”和“how”|CVPR 2017