九野的博客
九野的博客

POJ 3241 Object Clustering 二维平面曼哈顿距离最小生成树

题目链接：点击打开链接

题意：

给定二维平面上的n个点坐标，常数k

下面n行给出坐标

求一个最小生成树，问第k大的边是多少。

任意两个点间建一条边的花费是其曼哈顿距离。

思路：转自：点击打开链接

一、曼哈顿距离最小生成树

曼哈顿距离最小生成树问题可以简述如下：

给定二维平面上的N个点，在两点之间连边的代价为其曼哈顿距离，求使所有点连通的最小代价。

朴素的算法可以用O(N2)的Prim，或者处理出所有边做Kruskal，但在这里总边数有O(N2)条，所以Kruskal的复杂度变成了O(N2logN)。

但是事实上，真正有用的边远没有O(N2)条。我们考虑每个点会和其他一些什么样的点连边。可以得出这样一个结论，以一个点为原点建立直角坐标系，在每45度内只会向距离该点最近的一个点连边。

这个结论可以证明如下：假设我们以点A为原点建系，考虑在y轴向右45度区域内的任意两点B(x1,y1)和C(x2,y2)，不妨设|AB|≤|AC|（这里的距离为曼哈顿距离），如下图：


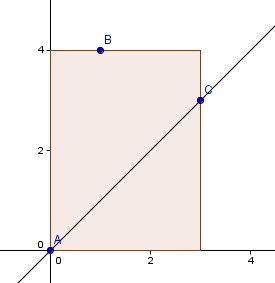
|AB|=x1+y1，|AC|=x2+y2，|BC|=|x1-x2|+|y1-y2|。而由于B和C都在y轴向右45度的区域内，有y-x>0且x>0。下面我们分情况讨论：

1.      x1>x2且y1>y2。这与|AB|≤|AC|矛盾；

2.      x1≤x2且y1>y2。此时|BC|=x2-x1+y1-y2，|AC|-|BC|=x2+y2-x2+x1-y1+y2=x1-y1+2*y2。由前面各种关系可得y1>y2>x2>x1。假设|AC|<|BC|即y1>2*y2+x1，那么|AB|=x1+y1>2*x1+2*y2，|AC|=x2+y2<2*y2<|AB|与前提矛盾，故|AC|≥|BC|；

3.      x1>x2且y1≤y2。与2同理；

4.      x1≤x2且y1≤y2。此时显然有|AB|+|BC|=|AC|，即有|AC|>|BC|。

综上有|AC|≥|BC|，也即在这个区域内只需选择距离A最近的点向A连边。

这种连边方式可以保证边数是O(N)的，那么如果能高效处理出这些边，就可以用Kruskal在O(NlogN)的时间内解决问题。下面我们就考虑怎样高效处理边。

我们只需考虑在一块区域内的点，其他区域内的点可以通过坐标变换“移动”到这个区域内。为了方便处理，我们考虑在y轴向右45度的区域。在某个点A(x0,y0)的这个区域内的点B(x1,y1)满足x1≥x0且y1-x1>y0-x0。这里对于边界我们只取一边，但是操作中两边都取也无所谓。那么|AB|=y1-y0+x1-x0=(x1+y1)-(x0+y0)。在A的区域内距离A最近的点也即满足条件的点中x+y最小的点。因此我们可以将所有点按x坐标排序，再按y-x离散，用线段树或者树状数组维护大于当前点的y-x的最小的x+y对应的点。时间复杂度O(NlogN)。

至于坐标变换，一个比较好处理的方法是第一次直接做；第二次沿直线y=x翻转，即交换x和y坐标；第三次沿直线x=0翻转，即将x坐标取相反数；第四次再沿直线y=x翻转。注意只需要做4次，因为边是双向的。

至此，整个问题就可以在O(NlogN)的复杂度内解决了。


#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
const int inf = 1e8;
const double eps = 1e-8;
const double pi = acos(-1.0);
template 
inline bool rd(T &ret) {
	char c; int sgn;
	if (c = getchar(), c == EOF) return 0;
	while (c != '-' && (c<'0' || c>'9')) c = getchar();
	sgn = (c == '-') ? -1 : 1;
	ret = (c == '-') ? 0 : (c - '0');
	while (c = getchar(), c >= '0'&&c <= '9') ret = ret * 10 + (c - '0');
	ret *= sgn;
	return 1;
}
template 
inline void pt(T x) {
	if (x <0) { putchar('-'); x = -x; }
	if (x>9) pt(x / 10);
	putchar(x % 10 + '0');
}
using namespace std;
const int N = 1e5 + 10;

class MST{
	struct Edge{
		int from, to, dis;
		Edge(int _from = 0, int _to = 0, int _dis = 0) :from(_from), to(_to), dis(_dis){}
		bool operator < (const Edge &x) const{
			return dis < x.dis;
		}
	}edge[N << 3];
	int f[N], tot;
	int find(int x){ return x == f[x] ? x : f[x] = find(f[x]); }
	bool Union(int x, int y){
		x = find(x); y = find(y);
		if (x == y)return false;
		if (x > y)swap(x, y);
		f[x] = y;
		return true;
	}
public:
	void init(int n){
		for (int i = 0; i <= n; i++)f[i] = i;
		tot = 0;
	}
	void add(int u, int v, int dis){
		edge[tot++] = Edge(u, v, dis);
	}
	int work(){
		sort(edge, edge + tot);
		int cost = 0;
		for (int i = 0; i < tot; i++){
			if (Union(edge[i].from, edge[i].to))
				cost += edge[i].dis;
		}
		return cost;
	}
	int work_kth(int k){
		sort(edge, edge + tot);
		int cost = 0;
		for (int i = 0; i < tot && k; i++){
			if (Union(edge[i].from, edge[i].to))
				cost = edge[i].dis, k--;
		}
		return cost;
	}
}mst;
struct Point{
	int x, y, id;
	friend bool operator<(const Point&a, const Point&b){
		if (a.x == b.x)return a.y < b.y;
		return a.x < b.x;
	}
}p[N];
class BIT{
	int c[N], id[N], maxn;
	int lowbit(int x){ return x&-x; }
public:
	void init(int n){
		maxn = n + 10;
		fill(c, c + maxn + 1, inf);
		fill(id, id + maxn + 1, -1);
	}
	void updata(int pos, int val, int _id){
		while (pos){
			if (c[pos] > val){ c[pos] = val; id[pos] = _id; }
			pos -= lowbit(pos);
		}
	}
	int query(int pos){
		int val = inf, _id = -1;
		while (pos <= maxn){
			if (val > c[pos]){ val = c[pos]; _id = id[pos]; }
			pos += lowbit(pos);
		}
		return _id;
	}
}tree;
inline bool cmp(int *x, int *y){ return *x < *y; }
class Manhattan_MST{
	int *po[N], a[N]; 
public:
	int work(int l, int r, int k){
		mst.init(r);
		for (int dir = 1; dir <= 4; dir++){
			if (dir%2==0)for (int i = l; i <= r; i++)swap(p[i].x, p[i].y);
			else if (dir == 3)for (int i = l; i <= r; i++)p[i].x = -p[i].x;
			sort(p + l, p + r + 1);
			for (int i = l; i <= r; ++i) a[i] = p[i].y - p[i].x, po[i] = &a[i];
			sort(po + l, po + r + 1, cmp);
			for (int i = l; i <= r; i++)*po[i] = i;
			tree.init(r);
			for (int i = r; i >= l; i--)
			{
				int id = tree.query(a[i]);
				if (id != -1)
					mst.add(p[i].id, p[id].id, abs(p[i].x - p[id].x) + abs(p[i].y - p[id].y));
				tree.updata(a[i], p[i].x + p[i].y, i);
			}
		}
		return mst.work_kth(k);
	}
}m_mst;

int n, k;
int main(){
	rd(n); rd(k);
	for (int i = 1; i <= n; i++)rd(p[i].x), rd(p[i].y), p[i].id = i;
	pt(m_mst.work(1, n, n-k)); puts("");
	return 0;
}



你可能感兴趣的:(生成树,莫队算法)

  • 数据结构应用实例(四)——最小生成树 cyzhou1221 数据结构基础数据结构
    Content：一、问题描述二、算法思想三、代码实现四、两种算法的比较五、小结一、问题描述  利用prim算法和kruskal算法实现最小生成树问题；二、算法思想  首先判断图是否连通，只有在连通的情况下才进行最小树的生成；三、代码实现#include#include#include#definemaxx999999#pragmawarning(disable:4996)typedefstruct
  • 数据结构与算法 - 贪心算法 临界点oc 数据结构与算法贪心算法算法
    一、贪心例子贪心算法或贪婪算法的核心思想是：1.将寻找最优解的问题分为若干个步骤2.每一步骤都采用贪心原则，选取当前最优解3.因为没有考虑所有可能，局部最优的堆叠不一定让最终解最优贪心算法是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是最好或最优的算法。这种算法通常用于求解优化问题，如最小生成树、背包问题等。贪心算法的应用：1.背包问题：给定一组物品和一个背包
  • C语言数据结构克鲁斯卡尔算法-求最小生成树 Yetteego 数据结构与算法（c语言）c语言C语言数据结构
    /**克鲁斯卡尔算法*得到图的最小生成树*构造一个无向网的的邻接矩阵*创建一个临时数组*对edge数组进行排序*/#include#include#includetypedefchar*VertexType;//顶点的信息的数据类型typedefintArcType;//权重胡数据类型#defineVERTEXNUM100//最大顶点数#defineMAX_INT32726//权重的无限大取值#d
  • 最短路算法一 halcyonfreed 算法
    2024061819:33朴素版Dijkstra47:00Heap优化版1:04:00Bellman-ford最短路算法——5种！！！考察重点：不会考算法证明，这里不讲了，重点是实现+抽象1.如何建图——如何定义点边，抽象成一个图问题Prim/i/，kruskal是最小生成树算法不是prime/ai/质数1.是么时候用？方法n图的node数m边数单源：只有一个起点，求从1个点到其他所有点/第n号点
  • BZOJ-2521: [Shoi2010]最小生成树（最小割）（本蒟蒻的BZOJ第401 AC撒花~） AmadeusChan
    题目：http://www.lydsy.com/JudgeOnline/problem.php?id=2521挺神奇的一个最小割模型，如果要使得该边一定在MST上，那么要保证该边连接的两个连通块之间不存在其他边权小于等于它的边，那么自然就最小割啦。代码：#include#include#includeusingnamespacestd;#definemaxn1010#definemaxv1010#
  • 无向图的连通分量 小凳子在线 图论
    读入一个无向图的邻接矩阵（即数组表示），建立无向图并按照以上描述中的算法建立无向图的生成森林。对于森林中的每一棵生成树，遍历所有顶点，并输出遍历顶点的顺序。输入输入的第一行包含一个正整数n，表示图中共有n个顶点。其中n不超过50。以后的n行中每行有n个用空格隔开的整数0或1，对于第i行的第j个0或1，1表示第i个顶点和第j个顶点有直接连接，0表示没有直接连接。当i和j相等的时候，保证对应的整数为0
  • 华为 HCIP-Datacom H12-821 题库 (1) 可惜已不在 HCIP华为网络
    有需要题库的可以看主页置顶需要题库的加Q裙V群仅进行学习交流1.MSTP有不同的端口角色，对此说法不正确的是：A、MSTP中除边缘端口外，其他端口角色都参与MSTP的计算过程B、MSTP同一端口在不同的生成树实例中可以担任不同的角色。C、MSTP域边缘端口是指位于MST域的边缘并连接其它MST域或SST的端口D、Backup端口作为根端口的备份，提供了从指定桥到根的另一条可切换路径答案：D解析：在
  • 数据结构-二叉树的遍历和线索二叉树 0X78 C语言各问题解决方法数据结构数据结构算法
    一、了解二叉树遍历1.先序遍历定义：先序遍历是指在访问一个节点时，先访问该节点本身，然后再访问其左子树和右子树。顺序：访问根节点先序遍历左子树先序遍历右子树示例：假设有如下二叉树：A/\BC/\DE先序遍历的结果为：A,B,D,E,C应用：先序遍历通常用于复制树结构或生成树的前缀表达式。2.中序遍历定义：中序遍历是指在访问一个节点时，先访问其左子树，然后访问该节点本身，最后访问其右子树。顺序：中序
  • MSTP多实例生成树（华为） 期待未来的男孩 路由交换网络
    目录MSTP简介定义目的MSTP基本概念MSTP的网络层次MST域（MSTRegion）MSTP报文MSTP报文格式MSTP拓扑计算优先级向量CIST的计算MSTI的计算MSTP快速收敛机制配置MSTP+VRRP组合组网示例配置思路操作步骤MSTP简介定义多生成树协议MSTP（MultipleSpanningTreeProtocol）是IEEE802.1s中定义的生成树协议，通过生成多个生成树，来
  • 并查集【算法 12】 终末圆 算法算法cc++python数据结构acmc语言
    并查集(Union-Find)的基础概念与实现并查集（Union-Find）是一种用于处理不相交集合（disjointsets）的数据结构，常用于解决连通性问题。典型的应用场景包括动态连通性问题（如网络节点连通性检测）、图论中的最小生成树（Kruskal算法）、社交网络中的群体归属等。并查集的两大基本操作合并操作(Union):将两个不同的集合合并为一个集合。查找操作(Find):查询某个元素属于
  • 探索贪心算法：解决优化问题的高效策略 快乐非自愿 贪心算法算法
    贪心算法是一种在每一步选择中都采取当前最佳选择的算法，以期在整体上达到最优解。它广泛应用于各种优化问题，如最短路径、最小生成树、活动选择等。本文将介绍贪心算法的基本概念、特点、应用场景及其局限性。贪心算法的基本概念贪心算法的核心思想是局部最优策略，即在每一步选择中都选择当前看起来最优的选项，希望通过一系列的局部最优选择达到全局最优。贪心算法的特点局部最优选择：每一步都选择当前状态下最优的操作。无需
  • 数据结构——第六章 图 疯子书生z 数据结构数据结构
    [知识框架]主要掌握深度优先搜索和广度优先搜索，图的基本概念及基本性质、图的存储结构（邻接矩阵、邻接表、邻接多重表和十字链表）及其特性、存储结构之间的转化、基于存储结构上的遍历操作和各种应用（拓扑排序、最小生成树、最短路径和关键路径）等。通常要求掌握基本思想和实现步骤（手动模拟）。6.1图的基本概念6.1.1图的定义图GGG由顶点集VVV和边集EEE组成，记为G=(V,E)G=(V,E)G=(V,
  • 简单の暑假总结——最小生成树 C2024XSC184 笔记
    6.1最小生成树我们先来了解一下最小生成树的概念：我们定义无向连通图的最小生成树（MinimumSpanningTree，MST）为边权和最小的生成树（树也叫做生成树）。——OIWiki我们举一个例子：在这样一个带权无向图中，它的最小生成树如下图所示，其权值为141414我们有222种算法来解决这个问题6.2Prim算法Prim算法无论是本质上还是代码上都与Dijkstra高度类似，本质上还是一个
  • 单调栈 LeetCode 1130. 叶值的最小代价生成树 EQUINOX1 OJ刷题解题报告leetcode算法动态规划
    目录一、题目1、题目描述2、输入输出2.1输入2.2输出3、原题链接二、解题报告1、思路分析2、复杂度3、代码详解一、题目1、题目描述给你一个正整数数组arr，考虑所有满足以下条件的二叉树：每个节点都有0个或是2个子节点。数组arr中的值与树的中序遍历中每个叶节点的值一一对应。每个非叶节点的值等于其左子树和右子树中叶节点的最大值的乘积。在所有这样的二叉树中，返回每个非叶节点的值的最小可能总和。这个
  • STP---生成树协议 보고.싶다 hcipphp服务器开发语言
    STP的作用a)Stp通过阻塞端口来消除环路，并能够实现链路备份目的b)消除了广播风暴c)物理链路冗余，网络变成了层次化结构的网络STP操作选举一个根桥每个非根交换机选举一个根端口每个网段选举一个指定端口阻塞非根，非指定端口STP--生成树协议：作用专门设计出来解决二层环路问题的协议线路冗余设备冗余交换机的广播风暴：洪范的数据帧在交换机之间来回循环发送，浪费资源MAC地址表的偏移多帧复制交换机会逻
  • 最小生成树 - Kruskal算法 我想进大厂 算法c++图论
    kruskal算法---求稀疏图的最小生成树步骤1，将所有边按权重从大到小排序，调用系统的sort函数2，枚举每条边a、b,权重cif(a、b不联通)就将这条边加入集合中输入格式第一行包含两个整数n和m。接下来m行，每行包含三个整数u，v，w，表示点u和点v之间存在一条权值为w的边。输出格式共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出impos
  • 图与树的基本概念 小魏冬琅 其他算法
    目录引言图与树结构的重要性图的基本概念图的表示方式图的遍历算法树的基本概念树的定义与性质树的遍历二叉树与多叉树的概念图与树的高级应用最短路径算法最小生成树算法总结与应用综合实例分析引言在计算机科学的世界中，图和树是两种非常重要的数据结构。它们不仅在理论上有着广泛的研究价值，更是在实际编程中广泛应用于网络通信、路径规划、数据库索引等领域。通过深入理解图与树的基本结构与算法，我们可以更高效地解决许多复
  • 算法学习6——贪心算法 零 度° 算法学习算法学习贪心算法
    什么是贪心算法？贪心算法是一种在每一步选择中都采取当前状态下最优或最有利的选择的算法。其核心思想是通过一系列局部最优选择来达到全局最优解。贪心算法广泛应用于各种优化问题，如最短路径、最小生成树、背包问题等。贪心算法的特点局部最优选择：每一步都做出在当前情况下最优的选择。无后效性：一旦某个状态被确定，就不会再被改变或回溯。逐步构造解决方案：通过一系列的选择逐步构建出最终的解决方案。经典例子及其Pyt
  • eNSP学习——RSTP基础配置 TXFBAP #交换机相关华为学习网络华为
    目录知识储备实验内容：实验目的：实验步骤：实验拓扑实验编址MAC地址表实验步骤一、基本配置二、配置RSTP基本功能三、配置边缘端口四、查看备份端口状态需要完整的配置命令大全的可以点击链接自取：华为ｅNSP各种设备配置命令大全PDF版资源-CSDN文库RSTP协议是对STP的升级，它重新划定端口的角色及状态，使用更快速的握手协商机制，降低了收敛时间，使它成为继STP协议后首选的生成树协议，不足之处就
  • 华为---RSTP（一）---RSTP简介 义一 网络华为网络
    目录1.STP（SpanningTreeProtocol，生成树协议）的作用2.STP的缺点2.1STP网络拓扑收敛慢2.2STP网络链路故障，端口状态切换慢2.3终端链路参与STP网络运算，浪费网络资源2.4STP网络拓扑变更机制复杂，效率低下2.5STP交换机端口角色偏少，角色转换缓慢2.6STP交换机端口状态偏多3.RSTP和STP的不同之处4.RSTP和STP端口状态对比5.RSTP的端口
  • pku acm 题目分类 moxiaomomo 算法数据结构numbers优化calendarcombinations
    1.搜索//回溯2.DP（动态规划）3.贪心北大ACM题分类2009-01-2714.图论//Dijkstra、最小生成树、网络流5.数论//解模线性方程6.计算几何//凸壳、同等安置矩形的并的面积与周长sp;7.组合数学//Polya定理8.模拟9.数据结构//并查集、堆sp;10.博弈论1、排序sp;1423,1694,1723,1727,1763,1788,1828,1838,1840,22
  • 蓝桥杯：C++贪心算法、字符串函数、朴素模式匹配算法、KMP算法 DaveVV 蓝桥杯c++蓝桥杯c++贪心算法算法开发语言数据结构c语言
    贪心算法贪心(Greedy)算法的原理很容易理解：把整个问题分解成多个步骤，在每个步骤都选取当前步骤的最优方案，直到所有步骤结束；每个步骤都不考虑对后续步骤的影响，在后续步骤中也不再回头改变前面的选择。贪心算法虽然简单，但它有广泛的应用。例如图论中的最小生成树(MinimalSpanningTree，MST)算法、单源最短路径算法(Dijkstra)都是贪心算法的典型应用。贪心算法的主要问题是不一
  • 【数据结构】图 rygttm 数据结构数据结构算法
    文章目录图1.图的两种存储结构2.图的两种遍历方式3.最小生成树的两种算法（无向连通图一定有最小生成树）4.单源最短路径的两种算法5.多源最短路径图1.图的两种存储结构1.图这种数据结构相信大家都不陌生，实际上图就是另一种多叉树，每一个结点都可以向外延伸许多个分支去连接其他的多个结点，而在计算机中表示图其实很简单，只需要存储图的各个结点和结点之间的联系即可表示一个图，顶点可以采取数组vector存
  • 软考30-上午题-数据结构-小结 ruleslol 软考中级学习笔记
    一、杂题汇总真题1：有向图——AOV带权有向图——AOE真题2：二叉排序树：左子树<根节点<右子树。二叉排序树中序遍历，节点关键字有序（递增）；关键字初始序列有序，二叉树是单支树。（无序，也可以是单支树）真题3：真题4：真题5：真题6：真题7：prim算法，时间复杂度为：O(n^2)，n为图的顶点数。该算法的计算时间与图中的边数无关，所以，该算法适合边稠密的图的最小生成树。kruscal算法，时间
  • 根据邻接表画广度优先生成树和深度优先生成树 Just right 深度优先宽度优先算法
    不保证正确，也希望你们发现错误在评论区评论题目画出邻接表，根据邻接表写出从V1开始的广度优先遍历序列画出广度优先生成树广度优先遍历序列V1V2V4V3广度优先生成树深度优先遍历序列V1V2V3V4深度优先生成树
  • 备战蓝桥杯---图论之最小生成树 CoCoa-Ck 图论算法蓝桥杯c++笔记
    首先，什么是最小生成树？他就是无向图G中的所有生成树中树枝权值总和最小的。如何求？我们不妨采用以下的贪心策略：Prim算法（复杂度：（n+m)logm)：我们对于把上述的点看成两个集合，一个是确定了最小生成树的点，一个还没有确定，我们只要不断把距离已经确定的集合的最短的边添加进去即可。假如我们加的距离不是最小的，那么当我们假设未确定的点已经构成了他们点的最小生成树，那么我们此时用距离最小的去添加他
  • HCIA~HCIE个人笔记索引 Hades_Ling HCIA相关知识HCIP相关知识华为网络
    HCIA~HCIE个人笔记索引HCIA部分(2022.11.27~2022.12.19)1.0.0华为设备telnet与ssh的配置1.1.0华为设备FTP服务器2.0.0以太网CSMA-CD与CSMA-CA的区别与工作方式2.1.0以太网以太网帧格式与报文分片2.10.0以太网传统STP生成树（简介、工作方式）2.10.1以太网传统STP生成树（STPBPDU、STP端口状态、STP工作过程）2
  • 最小生成树详解(Prim算法/Kruskal算法) Stephen_Curry___ 算法c++c语言数据结构图搜索算法
    最小生成树⭐今天为大家带来的是最小生成树算法⭐在学习之前首先要搞清楚什么是最小生成树？给定一张边带权的无向图G=(V,E)，其中V表示途中点的集合，E表示途中边的集合，=|V|，m=|E|。由V中的全部n个顶点和E中n-1条边构成的无向连通子图被称为G的以可生成树，其中边的权重之和最小被称为无向图G的最小生成树。所以最小生成树是用来计算最小边权问题。⭐最小生成树最常用的有两种算法：Prim算法（解
  • 学习总结16 GGJJM 学习
    #【模板】最小生成树##题目描述如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出`orz`。##输入格式第一行包含两个整数N,M，表示该图共有N个结点和M条无向边。接下来M行每行包含三个整数Xi,Yi,Zi，表示有一条长度为Zi的无向边连接结点Xi,Yi。##输出格式如果该图连通，则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出`orz`。##样例#1###样例输入#
  • 2.13学习总结 啊这泪目了 学习
    1.出差（Bleeman—ford）（spfa）（dijkstra）2.最小生成树（prim）（Kruskal）最短路问题：出差https://www.luogu.com.cn/problem/P8802题目描述AA国有�N个城市，编号为1…�1…N小明是编号为11的城市中一家公司的员工，今天突然接到了上级通知需要去编号为�N的城市出差。由于疫情原因，很多直达的交通方式暂时关闭，小明无法乘坐飞机直
  • java杨辉三角 3213213333332132 java基础
    package com.algorithm; /** * @Description 杨辉三角 * @author FuJianyong * 2015-1-22上午10:10:59 */ public class YangHui { public static void main(String[] args) { //初始化二维数组长度 int[][] y
  • 《大话重构》之大布局的辛酸历史 白糖_ 重构
    《大话重构》中提到“大布局你伤不起”，如果企图重构一个陈旧的大型系统是有非常大的风险，重构不是想象中那么简单。我目前所在公司正好对产品做了一次“大布局重构”，下面我就分享这个“大布局”项目经验给大家。   背景         公司专注于企业级管理产品软件，企业有大中小之分，在2000年初公司用JSP/Servlet开发了一套针对中
  • 电驴链接在线视频播放源码 dubinwei 源码电驴播放器视频ed2k
    本项目是个搜索电驴（ed2k）链接的应用,借助于磁力视频播放器（官网： http://loveandroid.duapp.com/ 开放平台），可以实现在线播放视频，也可以用迅雷或者其他下载工具下载。 项目源码： http://git.oschina.net/svo/Emule,动态更新。也可从附件中下载。 项目源码依赖于两个库项目，库项目一链接： http://git.oschina.
  • Javascript中函数的toString()方法 周凡杨 JavaScriptjstoStringfunctionobject
    简述     The toString() method returns a string representing the source code of the function.     简译之，Javascript的toString()方法返回一个代表函数源代码的字符串。 句法     function.
  • struts处理自定义异常 g21121 struts
    很多时候我们会用到自定义异常来表示特定的错误情况，自定义异常比较简单，只要分清是运行时异常还是非运行时异常即可，运行时异常不需要捕获，继承自RuntimeException，是由容器自己抛出，例如空指针异常。 非运行时异常继承自Exception，在抛出后需要捕获，例如文件未找到异常。 此处我们用的是非运行时异常，首先定义一个异常LoginException: /** * 类描述：登录相
  • Linux中find常见用法示例 510888780 linux
    Linux中find常见用法示例 ·find   path   -option   [   -print ]   [ -exec   -ok   command ]   {} \; find命令的参数；
  • SpringMVC的各种参数绑定方式 Harry642 springMVC绑定表单
    1. 基本数据类型(以int为例，其他类似)： Controller代码： @RequestMapping("saysth.do") public void test(int count) { } 表单代码： <form action="saysth.do" method="post&q
  • Java 获取Oracle ROWID aijuans javaoracle
    A ROWID is an identification tag unique for each row of an Oracle Database table. The ROWID can be thought of as a virtual column, containing the ID for each row. The oracle.sql.ROWID class i
  • java获取方法的参数名 antlove javajdkparametermethodreflect
    reflect.ClassInformationUtil.java package reflect; import javassist.ClassPool; import javassist.CtClass; import javassist.CtMethod; import javassist.Modifier; import javassist.bytecode.CodeAtt
  • JAVA正则表达式匹配 查找 替换 提取操作 百合不是茶 java正则表达式替换提取查找
    正则表达式的查找;主要是用到String类中的split();       String str;      str.split();方法中传入按照什么规则截取,返回一个String数组   常见的截取规则: str.split("\\.")按照.来截取 str.
  • Java中equals()与hashCode()方法详解 bijian1013 javasetequals()hashCode()
    一.equals()方法详解     equals()方法在object类中定义如下：  public boolean equals(Object obj) { return (this == obj); }    很明显是对两个对象的地址值进行的比较（即比较引用是否相同）。但是我们知道，String 、Math、I
  • 精通Oracle10编程SQL(4)使用SQL语句 bijian1013 oracle数据库plsql
    --工资级别表 create table SALGRADE ( GRADE NUMBER(10), LOSAL NUMBER(10,2), HISAL NUMBER(10,2) ) insert into SALGRADE values(1,0,100); insert into SALGRADE values(2,100,200); inser
  • 【Nginx二】Nginx作为静态文件HTTP服务器 bit1129 HTTP服务器
     Nginx作为静态文件HTTP服务器 在本地系统中创建/data/www目录，存放html文件(包括index.html) 创建/data/images目录，存放imags图片 在主配置文件中添加http指令   http { server { listen 80; server_name
  • kafka获得最新partition offset blackproof kafkapartitionoffset最新
    kafka获得partition下标，需要用到kafka的simpleconsumer   import java.util.ArrayList; import java.util.Collections; import java.util.Date; import java.util.HashMap; import java.util.List; import java.
  • centos 7安装docker两种方式 ronin47
          第一种是采用yum 方式              yum install -y docker           
  • java-60-在O(1)时间删除链表结点 bylijinnan java
    public class DeleteNode_O1_Time { /** * Q 60 在O(1)时间删除链表结点 * 给定链表的头指针和一个结点指针(!!)，在O(1)时间删除该结点 * * Assume the list is: * head->...->nodeToDelete->mNode->nNode->..
  • nginx利用proxy_cache来缓存文件 cfyme cache
    user  zhangy users; worker_processes 10; error_log  /var/vlogs/nginx_error.log  crit; pid        /var/vlogs/nginx.pid; #Specifies the value for ma
  • [JWFD开源工作流]JWFD嵌入式语法分析器负号的使用问题 comsci 嵌入式
        假如我们需要用JWFD的语法分析模块定义一个带负号的方程式，直接在方程式之前添加负号是不正确的，而必须这样做：     string str01 = "a=3.14;b=2.71;c=0;c-((a*a)+(b*b))"     定义一个0整数c,然后用这个整数c去
  • 如何集成支付宝官方文档 dai_lm android
    官方文档下载地址 https://b.alipay.com/order/productDetail.htm?productId=2012120700377310&tabId=4#ps-tabinfo-hash 集成的必要条件 1. 需要有自己的Server接收支付宝的消息 2. 需要先制作app，然后提交支付宝审核，通过后才能集成 调试的时候估计会真的扣款，请注意
  • 应该在什么时候使用Hadoop datamachine hadoop
    原帖地址：http://blog.chinaunix.net/uid-301743-id-3925358.html 存档，某些观点与我不谋而合，过度技术化不可取，且hadoop并非万能。 --------------------------------------------万能的分割线-------------------------------- 有人问我，“你在大数据和Hado
  • 在GridView中对于有外键的字段使用关联模型进行搜索和排序 dcj3sjt126com yii
    在GridView中使用关联模型进行搜索和排序 首先我们有两个模型它们直接有关联: class Author extends CActiveRecord { ... } class Post extends CActiveRecord { ... function relations() { return array( '
  • 使用NSString 的格式化大全 dcj3sjt126com Objective-C
    格式定义The format specifiers supported by the NSString formatting methods and CFString formatting functions follow the IEEE printf specification; the specifiers are summarized in Table 1. Note that you c
  • 使用activeX插件对象object滚动有重影 蕃薯耀 activeX插件滚动有重影
      使用activeX插件对象object滚动有重影   <object style="width:0;" id="abc" classid="CLSID:D3E3970F-2927-9680-BBB4-5D0889909DF6" codebase="activex/OAX339.CAB#
  • SpringMVC4零配置 hanqunfeng springmvc4
    基于Servlet3.0规范和SpringMVC4注解式配置方式，实现零xml配置，弄了个小demo，供交流讨论。     项目说明如下： 1.db.sql是项目中用到的表，数据库使用的是oracle11g 2.该项目使用mvn进行管理，私服为自搭建nexus,项目只用到一个第三方 jar，就是oracle的驱动； 3.默认项目为零配置启动，如果需要更改启动方式，请
  • 《开源框架那点事儿16》：缓存相关代码的演变 j2eetop 开源框架
    问题引入 上次我参与某个大型项目的优化工作，由于系统要求有比较高的TPS，因此就免不了要使用缓冲。 该项目中用的缓冲比较多，有MemCache，有Redis，有的还需要提供二级缓冲，也就是说应用服务器这层也可以设置一些缓冲。 当然去看相关实现代代码的时候，大致是下面的样子。 [java] view plain copy print ? public vo
  • AngularJS浅析 kvhur JavaScript
    概念 AngularJS is a structural framework for dynamic web apps. 了解更多详情请见原文链接：http://www.gbtags.com/gb/share/5726.htm Directive 扩展html，给html添加声明语句，以便实现自己的需求。对于页面中html元素以ng为前缀的属性名称，ng是angular的命名空间
  • 架构师之jdk的bug排查(一)---------------split的点号陷阱 nannan408 split
    1.前言.    jdk1.6的lang包的split方法是有bug的,它不能有效识别A.b.c这种类型,导致截取长度始终是0.而对于其他字符,则无此问题.不知道官方有没有修复这个bug. 2.代码 String[] paths = "object.object2.prop11".split("'"); System.ou
  • 如何对10亿数据量级的mongoDB作高效的全表扫描 quentinXXZ mongodb
      本文链接:  http://quentinXXZ.iteye.com/blog/2149440 一、正常情况下，不应该有这种需求 首先，大家应该有个概念，标题中的这个问题，在大多情况下是一个伪命题，不应该被提出来。要知道，对于一般较大数据量的数据库，全表查询，这种操作一般情况下是不应该出现的，在做正常查询的时候，如果是范围查询，你至少应该要加上limit。 说一下，
  • C语言算法之水仙花数 qiufeihu c算法
    /** * 水仙花数 */ #include <stdio.h> #define N 10 int main() { int x,y,z; for(x=1;x<=N;x++) for(y=0;y<=N;y++) for(z=0;z<=N;z++) if(x*100+y*10+z == x*x*x
  • JSP指令 wyzuomumu jsp
    jsp指令的一般语法格式： <%@ 指令名 属性 =”值 ” %> 常用的三种指令： page,include,taglib page指令语法形式： <%@ page 属性 1=”值 1” 属性 2=”值 2”%> include指令语法形式： <%@include file=”relative url”%> (jsp可以通过 include
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他