数字图像处理实验之图像压缩

1. 实验目的

1. 掌握图像信息熵的计算方法。
2. 理解霍夫曼编码和解码的基本步骤。
3. 掌握霍夫曼编码和解码的操作，编程实现。

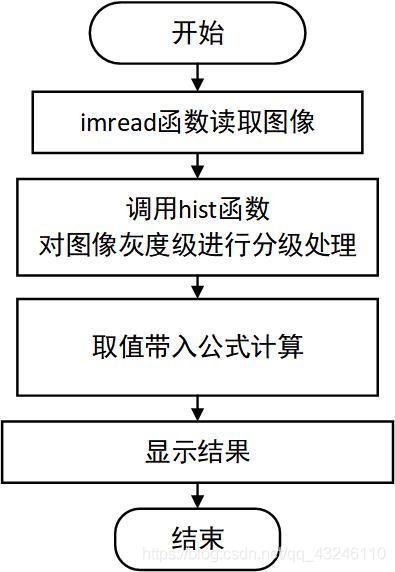
2. 实验流程

2.1 图像熵的计算

2.2 霍夫曼编码流程

2.3 霍夫曼编码函数

2.4 霍夫曼解码流程

3. 实验代码

3.1 计算图像熵

%% 计算熵
clear,clc,close ALL;
tic
f1=imread('task1/1.tif');
f2=imread('task1/2.tif');
f3=imread('task1/3.tif');
n=256;
%计算第一幅图的熵
x1=double(f1);
P1=hist(x1(:),n);
P1=P1/sum(P1(:));
i1=find(P1);
h1=-sum(P1(i1).*log2(P1(i1)));
%计算第二幅图的熵
x2=double(f2);
P2=hist(x2(:),n);
P2=P2/sum(P2(:));
i2=find(P2);
h2=-sum(P2(i2).*log2(P2(i2)));
%计算第三幅图的熵
x3=double(f3);
P3=hist(x3(:),n);
P3=P3/sum(P3(:));
i3=find(P3);
h3=-sum(P3(i3).*log2(P3(i3)));
figure;
subplot(131),imshow(f1),title(['图1的熵为：',num2str(h1)]);
subplot(132),imshow(f2),title(['图2的熵为：',num2str(h2)]);
subplot(133),imshow(f3),title(['图3的熵为：',num2str(h3)]);
toc

3.2 霍夫曼编码

%% 实现霍夫曼编码
clear,clc,close ALL;
tic
I=imread('task1/3.tif');
I=double(I);
[m,n]=size(I);m0=m/2;n0=n/2;
a=I(1:m0,1:n0);b=I(1:m0,n0:n);c=I(m0:m,1:n0);d=I(m0:m,n0:n);
j = 20;
I0=hist(I(:),j);I0=I0/sum(I0(:));
I1=hist(a(:),j);I1=I1/sum(I1(:));
I2=hist(b(:),j);I2=I2/sum(I2(:));
I3=hist(c(:),j);I3=I3/sum(I3(:));
I4=hist(d(:),j);I4=I4/sum(I4(:));
% 计算熵
i=find(I0);h = -sum(I0(i).*log2(I0(i)));
i1=find(I1);h1 = -sum(I1(i1).*log2(I1(i1)));
i2=find(I2);h2 = -sum(I2(i2).*log2(I2(i2)));
i3=find(I3);h3 = -sum(I3(i3).*log2(I3(i3)));
i4=find(I4);h4 = -sum(I4(i4).*log2(I4(i4)));
% 霍夫曼编码及计算编码效率
alph = huffman(I0);
alph1 = huffman(I1);
alph2 = huffman(I2);
alph3 = huffman(I3);
alph4 = huffman(I4);
 
for i=1:length(I0)
    [m,n]=size(char(alph(i)));
    l(i)=n;
end
for i1=1:length(I1)
    [m1,n1]=size(char(alph1(i1)));
    l1(i1)=n1;
end
for i2=1:length(I2)
    [m2,n2]=size(char(alph2(i2)));
    l2(i2)=n2;
end
for i3=1:length(I3)
    [m3,n3]=size(char(alph3(i3)));
    l3(i3)=n3;
end
for i4=1:length(I4)
    [m4,n4]=size(char(alph4(i4)));
    l4(i4)=n4;
end
disp(['图像熵为：',num2str(h)]);
disp(['分块后图像熵分别为：',num2str(h1),' ',num2str(h2),' ',num2str(h3),' ',num2str(h4)]);
p = sum(I0.*l);p1 = sum(I1.*l1);p2 = sum(I2.*l2);p3 = sum(I3.*l3);p4 = sum(I4.*l4);
disp(['平均编码长度为：',num2str(p)]);
disp(['分块后每部分平均编码长度为：',num2str(p1),' ',num2str(p2),' ',num2str(p3),' ',num2str(p4)]);
n = h/p; n1 = h1/p1; n2 = h2/p2; n3 = h3/p3; n4 = h4/p4;
disp(['分块后每部分的编码效率为：',num2str(n1),' ',num2str(n2),' ',num2str(n3),' ',num2str(n4)]);
nla = (h1+h2+h3+h4)/(p1+p2+p3+p4);
disp(['编码效率为：',num2str(n)]);
disp(['分块后编码效率为：',num2str(nla)]);
toc

3.3 霍夫曼编码函数

function CODE = huffman(p)
error(nargchk(1,1,nargin));
if(ndims(p) ~= 2) || min(size(p)) > 1 || ~isreal(p) ||~isnumeric(p)
    error('P must be a real numeric vector.');
end
global CODE
CODE = cell(length(p),1);
if length(p) > 1
    p = p/sum(p);
    s = reduce(p);
    makecode(s,[]);
else
    CODE = {'1'};
end
function s = reduce(p)
s = cell(length(p),1);
for i = 1:length(p)
    s{i} = i;
end
while numel(s) > 2
    [p,i] = sort(p);
    p(2) = p(1) + p(2);
    p(1) = [];
    s = s(i);
    s{2} = {s{1},s{2}};
    s(1) = [];
end
function makecode(sc,codeword)
global CODE
if isa(sc,'cell')
    makecode(sc{1},[codeword 0]);
    makecode(sc{2},[codeword 1]);
else
    CODE{sc} = char('0'+ codeword);
end

3.4 霍夫曼解码

%% 霍夫曼解码
clear,clc,close ALL;
tic
I = imread('task1\2.tif');
[M,N] = size(I);
I1 = I(:);
P = zeros(1,256);
%获取各符号的概率
for i = 0:255
    P(i+1) = length(find(I1 == i))/(M*N);
end
k = 0:255;
dict = huffmandict(k,P); %生成字典
enco = huffmanenco(I1,dict); %编码
deco = huffmandeco(enco,dict); %解码
Ide = col2im(deco,[M,N],[M,N],'distinct'); %把向量重新转换成图像块；
figure('Name','霍夫曼编解码效果图','NumberTitle','off');
subplot(1,2,1);imshow(I);title('原图');
subplot(1,2,2);imshow(uint8(Ide));title('解码图');
toc

4. 实验结果及分析

4.1 图像熵的计算

1、实验结果：

2、结果分析：
由上图，共图3.1(a)——图3.1©三幅图。
其中熵的计算结果即如上表示，分别为0，8和7.3177。由上图可反应熵的概念，当灰度完全相同时，也就说明了熵值为零。

4.2 霍夫曼编码

1、实验结果

灰度级为20时，编码结果显示如下：

2、结果分析

本实验中，主要对图像进行了霍夫曼编码的实现和结果输出。
根据图3.2，可看出图像的熵、平均码长等信息，也反应出了分块前后编码效率的差异。
根据各个分块的导出信息，可以看出分块后的编码效率基本上都有所提高。在分块前编码效率为98.8%，分块编码后的效率为99.2%。也在一定程度上说明了分块编码能够解决的提高效率的问题。
霍夫曼编码结果如图3.3所示，可以看出编码的长度大小和之间的不同，也说明了程序运行的正确性，显示了霍夫曼树和霍夫曼编码的特点。

4.3 霍夫曼解码

1、实验结果

2、结果分析
本实验主要对编解码前后的图像进行了对比。如图3.4所示，两幅图相同。
通过实验的操作，编解码的实现。发现编码解码后的图像与原图相同，也就说明了霍夫曼编码为无损压缩，说明了霍夫曼编码的编码特点。