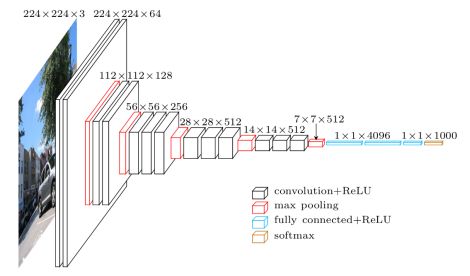
VGG：VERY DEEP CONVOLUTIONAL NETWORKS FOR LARGE-SCALE IMAGE RECOGNITION

论文地址：点击打开链接

翻译地址：点击打开链接

代码以及一些注释地址：点击打开链接

 

网络模型图：

                        

训练集预处理：

1.S即裁剪后的图片长度有：256和384 ，选其中一个把短边压缩到s然后用是s*s的框随机裁剪

2.s是裁剪后的图片长度在【256，512】之间，如果要裁剪的图片的长度不在范围内则进行裁剪，如果在范围内，则随机取一个值为s，然后进行裁剪

文中说是在梯度下降的时候对每张图随机裁剪一张。

基本配置：

     训练     kernel ：3*3  、 padding：1   、   stride：1   

               优化方法：带动量（momentum）的小批量梯度下降

               batch size：256

               learn rate： 0.01        和alexnet一样，如果val-acc不下降则学习率缩小十倍，训练过程缩小三次

               momentum ： 0.9

               weight decay（l2惩罚因子）：5*0.0001

               droupout rate （前两全连接层）：0.5

               目标函数：多项式logistic回归（softmax）

                迭代次数：37万

     测试：  kernel:   2*2.  、stride:   2

 

测试阶段：

测试阶段先对输入图像的短边rescale到预设尺度Q（测试图像的尺度），测试图像的尺寸Q和训练图像的尺寸S没必要完全一样。后文中作者提到对于每个训练图像的尺寸S，都有几个不同的Q来去预测，可以得到更好地性能。

原图比方左上角有个5×5的区域，crop出的224×224的左上角可以在里面移动（也就是说图像crop前，要resize到可以移动5×5格子的size，即224+5-1=228），另外加上水平翻转带来的可能性，那就是5x5x2=50种情况，作者总共在test阶段用了三个scale，即三个Q，那么一张图总共有150 crops。网络将会分别跑一张图的150个crops，然后将结果average，作者的150crops相比GoogLeNet（Szegedy et al. (2014)）的 4 scale的 144 crops（可以算一下，每个scale是36crops，如果其中包含水平翻转的话，那么就是18crops，可能是一个3×6的regular grid，类似的方法，因为没看文章这里只是猜测），并没有很大的性能提升。

也就是说作者认为裁剪带来的性价比是不值得的，而且只是在原图的左上角5*5范围内进行裁剪，感觉裁剪的效果也不是很好

 

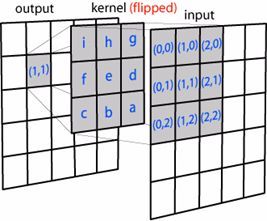
卷积过程：

                                   

 

 上面就是卷积一次的过程，在实际操作中卷积核是经过翻转180度的，然后在原图上进行内积。

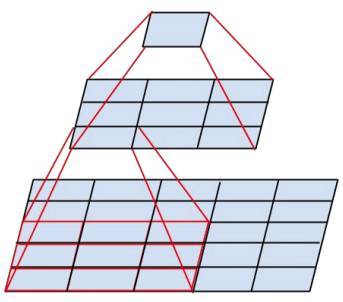
  下面说一个用投影的方式理解卷积：卷积过程就是图像每块patch和卷积核（原矩阵翻转180）的乘积和。把pathch和核均拉成一维向量，核扫描过程即内积，对于向量a[a1,a2,a3,a4],b[b1,b2,b3,b4]  内积又叫向量积、点乘，a点乘b=a1*b1+a2*b2+a3*b3+a4*b4 .物理意义即b在a方向上的投影。同样卷积过程便是图像在某个核方向上的投影，也就是在某个特征方向上的投影，就是把图像的表示的基变换了。

卷积过程的理解还可以参考下面这些网址  点击打开链接

 

1*1卷积核作用：

    1、降维（ dimension reductionality ）。比如，一张500 * 500且厚度depth为100 的图片在20个filter上做1*1的卷积，那么结       果的大小为500*500*20，当然也可以升维。

     2、加入非线性。卷积层之后经过激励层，1*1的卷积在前一层的学习表示上添加了非线性激励（ non-linear activation ），提 升网络的表达能力；主要是激励函数的作用。

 

全连接层作用：

   1.feature map 的维度变化

        随层数递增逐渐忽略局部信息，feature map的width和height随着每个pool操作缩小50%，5个pool操作使得width和height逐渐变化：224->112->56->28->14->7，但是深度depth（或说是channel数），随着5组卷积在每次增大一倍：3->64->128->256->512->512。特征信息从一开始输入 的  224x224x3被变换到7x7x512，从原本较为local的信息逐渐分摊到不同channel上，随着每次的conv和pool操作打散到channel层级上。

       我的理解是，这样便于后面fc层的特征映射，因为fc层相比conv更考虑全局信息，global的feature map（既有width，height还有channel）信息，  全部映射到4096维度。估算一下，也就是说7x7x512，大概是25000，映射到4096，大概是5000，就是说压缩到原来的五分之一。后面三个全连  接的理解是，这个映射过程的学习要慢点来，太快不易于捕捉特征映射来去之间的细微变化，让backprop学的更慢更细一些（更逐渐）。

        其实按理说不应该将feature map的维度与后面fc层的分析拆分开，毕竟最后的分类器是softmax，三个fc层的操作结束才是最终的feature map。   那么，最后一组卷积后就会接三组全连接层，前两组fc的形式是：fc4096-relu-dropout0.5（只有在全连接时用），最后一个fc的形式就是：                   fc1000。

         可以发现feature map的维度在最后一个卷积后达到7x7x512，即大概25000，紧接着压缩到4096维，可能是作者认为这个过程太急，又接一个  fc4096作为缓冲，同时两个fc4096后的relu又接dropout0.5去过渡这个过程，因为最后即将给1k-way softmax，所以又接了一个fc1000去降低               softmax的学习压力。

        feature map维度的整体变化过程是：先将local信息压缩，并分摊到channel层级，然后无视channel和local，通过fc这个变换再进一步压缩为稠密    的feature map，这样对于分类器而言有好处也有坏处，好处是将local信息隐藏于/压缩到feature map中，坏处是信息压缩都是有损失的，相当于          local信息被破坏了（分类器没有考虑到，其实对于图像任务而言，单张feature map上的local信息还是有用的）。   

 

 def fc_layer(self, bottom, name):
        with tf.variable_scope(name):
            shape = bottom.get_shape().as_list()
            print("************")
            print(bottom.get_shape().as_list())
            dim = 1
            for d in shape[1:]:
                dim *= d
            x = tf.reshape(bottom, [-1, dim])
            print(x)

            weights = self.get_fc_weight(name)
            biases = self.get_bias(name)
            print(weights)
            print(biases)
            print("&&&&&&&&&&")


            # Fully connected layer. Note that the '+' operation automatically
            # broadcasts the biases.
            fc = tf.nn.bias_add(tf.matmul(x, weights), biases)
            print(fc)

            return fc

卷积转换为全连接就是先计算出7*7*512=25008，然后乘上一个【25008，4096】的权值矩阵转化为4096大小，再加上4096维的偏置。

2.卷积组

 

除了卷积kernel和feature map的变化，卷积后的output channel数的变化是递增的（上面已经说过）。但是，若以pooling操作为切分点对整个网络分组的话，我们会得到五组卷积，五组卷积中有2种卷积组的形式，VGG网络是下面这样：

• 前两组卷积形式一样，每组都是：conv-relu-conv-relu-pool；
• 中间三组卷积形式一样，每组都是：conv-relu-conv-relu-conv-relu-pool；
• 最后三个组全连接fc层，前两组fc，每组都是：fc-relu-dropout；最后一个fc仅有fc。

CS231n的blog里将这种形式称为layer pattern，一般常见的网络都可以表示为：INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC的形式，其中，?表示pool是一个可选项。这样的pattern，因为可以对小卷积核stacking，更适合构建深层网络。INPUT -> FC表示一个线性分类器。

那么这VGG两种卷积组，即layer pattern的形式有什么区别，很明显第二种（[conv-relu]-[conv-relu]-[conv-relu]-pool）比第一种（[conv-relu]-[conv-relu]-pool） 多了一个[conv-relu]。我的理解是：

1. 多出的relu对网络中层进一步压榨提炼特征。结合一开始单张feature map的local信息更多一些，还没来得及把信息分摊到channel级别上，那么往后就慢慢以增大conv filter的形式递增地扩大channel数，等到了网络的中层，channel数升得差不多了（信息分摊到channel上得差不多了），那么还想抽local的信息，就通过再加一个[conv-relu]的形式去压榨提炼特征。有点类似传统特征工程中，已有的特征在固定的模型下没有性能提升了，那就用更多的非线性变换对已有的特征去做变换，产生更多的特征的意味；
2. 多出的conv对网络中层进一步进行学习指导和控制不要将特征信息漂移到channel级别上。
   1. 上一点更多的是relu的带来的理解，那么多出的[conv-relu]中conv的意味就是模型更强的对数据分布学习过程的约束力/控制力，做到信息backprop可以回传回来的学习指导。本身多了relu特征变换就加剧（权力释放），那么再用一个conv去控制（权力回收），也在指导网络中层的收敛；
   2. 其实conv本身关注单张feature map上的局部信息，也是在尝试去尽量平衡已经失衡的channel级别（depth）和local级别（width、height）之间的天平。这个conv控制着特征的信息量不要过于向着channel级别偏移。

 

3*3卷积核优势：

 

                                               

                                      两个3*3的卷积核卷积依次想当一个5*5的卷积核卷积一次

1⃣️3个激活函数（ReLU）去代替1个，可使决策函数更加具有辨别能力，此外就卷积本身的作用而言，3×3比7×7就足以捕获特征的变化：3×3的9个         格子，最中间的格子是一个感受野中心，可以捕获上下左右以及斜对角的特征变化。主要在于3个堆叠起来后，三个3×3近似一个7×7，网络深了两       层且多出了两个非线性ReLU函数，（特征多样性和参数参数量的增大，这里的参数增大和下面计算量说的参数不变不一样，下面是都有进行卷积         三次，而这里用3*3卷积三次和7*7卷积一次对比）使得网络容量更大（关于model capacity，AlexNet的作者认为可以用模型       的深度和宽度来控      制capacity），对于不同类别的区分能力更强（此外，从模型压缩角度也是要摒弃7×7，用更少的参数获得更深更宽的网络，也         一 定程度代表      着模型容量，后人也认为更深更宽比矮胖的网络好）；

2⃣️conv filter的参数减少。相比5×5、7×7和11×11的大卷积核，3×3明显地减少了参数量。作者还使用了1×1的卷积核，认为1×1卷积核是channel级别      的线性变换（毕竟一组channel用对应的一样的卷积核在这一组channel上扫描，一组channel不是指这一层feature map的所有channel）。比方            input  channel数和output channel数均为C，那么3层conv3x3卷积所需要的卷积层参数是：3x(Cx3x3xC)=27C^2，而一层conv7x7卷积所需要的卷        积层参数是：Cx7x7xC=49C^2。conv7x7的卷积核参数比conv3x3多了(49-27)/27×100% ≈ 81%；

3⃣️小卷积核代替大卷积核有正则作用。作者用三个conv3x3代替一个conv7x7，认为可以进一步分解（decomposition）原本用7×7大卷积核提到的特         征。

 

       

网络更深带来了更多变化，更好的特征多样性，就好比是数据增强虽然引来方差（可以理解为训练数据和训练标签的偏离程度）是好的，我们想在变化中寻找不变的映射关系。但是，网络更深带来特征更多真的好嘛？我觉得更多的特征和更深的网络，不一定都是有助于、有贡献于正确梯度下降寻找最优或者局部最优的方向，我们真正需要的是可以正确建立映射关系的特征。

反倒是层数越深，特征更多，会有更多局部最优。但为此，我们又在减少因引入特征多样性带来的高方差（也就是数据的分散程度，方差越大，数据分散分布）的影响，不论是在随机梯度下降中引入动量，还是各种正则化的手段，又尝试减少更深网络带来更多特征造成的影响。一方面我们在增大方差，又在减少方差。这样看，似乎这是矛盾的。

网络由于有着本身的更新策略，可以正确建立映射关系。但网络更深却在影响映射关系的建立，把这个建立的过程变得更加曲折，甚至无法建立出好的、正确的、有效的映射关系。

我想了想，感觉这是一个平衡，重要是多了可以筛选：
一方面，我们希望有更多特征，在于我们可以筛选。本身的更新策略可以指导映射关系的建立。但是学习的东西多了，必然会造成学习出现问题，因为要在其中筛选。但是所有的基于部分样本的优化带来的梯度估计，必然会学出的权重都有一点不正确。
另一方面，我们又在减少影响，减少不正确性带来的影响，就有这些正则化来去筛选。有的正则化起到筛选的作用，而有的则是减缓、减小高方差带来错误下降方向的影响的作用。

我觉得重点在于这个特征筛选做的好不好，现在大多情况都不缺数据。其实这样看来，即使是深度学习，又回到了以前的问题，特征工程、特征选择。似乎深度学习带来了更深的网络，表面上看给我们造成没有必要做特征工程的假象，但其实我们做了这个过程，在网络结构设计、模块选择、网络的训练（优化）trick里。

 

无论是特征跨depth的cross（resnet），还是跨channel的cross（lrn、shufflenet）。这几年的网络都是在网络更dense的前提（比方mobilenet）下，基于各自的module做特征工程，引入更多特征，一方面特征diverse方差加大，一方面又用正则等手段钝化平滑方差。我认为，大家认为深度学习玄学的一个原因可能是不可估量的方差的tradeoff造成的。

有小伙伴也提到，玄学也是因为现在的文章中说到的方法其实并不是work的，你按照他说的这么调整就是不对。

 

 池化层反向传播

 

 

反向的计算如下：

• max：反向过程会记录当时正向时最大值的位置，反向则最大值位置不变，其他位置填补0；
• average：反向过程会将正向的平均值，以平均的形式分摊到每个位置；
• stochastic：反向一样记录正向时时被随机选中的位置，该位置值不变，其他位置填补0。

 

网络可视化 ：这里推荐一个用于可视化的网址  点击打开链接

 

                打开链接以后把下面vgg16或者vgg19的prototxt复制到左边里面然后按shift+enter便可看到相应的网络图点击打开链接

finetune：

 作者还发现卷积网络是一个天然的十分优秀的特征提取器。浅层学到的是纹理特征，深层学到的是语意特征。也就是深层同一范围内矩阵的行和列的数量更多 。既然这样我们便可以fine-tune 网络的最后几层也就是对语意层进行重新训练使之适用我们的训练数据。先适用pretrained再在自己的小数据集上训练不容易过拟合。这里可以理解为：

 1⃣️一开始在量级大且多样性广的数据集上pre-train，不严谨的说法就是小数据只是当初pre-train 时所用的数据集的一个子集。 2⃣️模型已经见识过广泛的空间，这会带来更广阔和更丰富的特征空间，因而在小的数据集上训练时不会太纠结于比较片面或者倾斜的样本带来的影响，可以说是曾经沧海难为水吧。          

 

网络的参数表格

#	LAYER	FEATURE MAP	MEMORY	WEIGHTS
	INPUT	[224x224x3]	224x224x3=150K	0
1	CONV3-64	[224x224x64]	224x224x64=3.2M	(3x3x3)x64 = 1,7282
2	CONV3-64	[224x224x64]	224x224x64=3.2M	(3x3x64)x64 = 36,864
	POOL2	[112x112x64]	112x112x64=800K	0
3	CONV3-128	[112x112x128]	112x112x128=1.6M	(3x3x64)x128=73728
4	CONV3-128	[112x112x128]	112x112x128=1.6M	(3x3x128)x128=147456
	POOL2	[56x56x128]	56x56x128=400K	0
5	CONV3-256	[56x56x256]	56x56x256=800K	(3x3x128)x256=294912
6	CONV3-256	[56x56x256]	56x56x256=800K	(3x3x256)x256=589824
7	CONV3-256	[56x56x256]	56x56x256=800K	(3x3x256)x256=589824
	POOL2	[28x28x256]	28x28x256=200K	0
8	CONV3-512	[28x28x512]	28x28x512=400K	(3x3x256)x512=1179648
9	CONV3-512	[28x28x512]	28x28x512=400K	(3x3x512)x512=2359296
10	CONV3-512	[28x28x512]	28x28x512=400K	(3x3x512)x512=2359296
	POOL2	[14x14x512]	14x14x512=100K	0
11	CONV3-512	[14x14x512]	14x14x512=100K	(3x3x512)x512=2359296
12	CONV3-512	[14x14x512]	14x14x512=100K	(3x3x512)x512=2359296
13	CONV3-512	[14x14x512]	14x14x512=100K	(3x3x512)x512=2359296
	POOL2	[7x7x512]	7x7x512=25K	0
14	FC	[1x1x4096]	4096	7x7x512x4096=102760448
15	FC	[1x1x4096]	4096	4096×4096=16777216
16	FC	[1x1x1000]	1000	4096×1000=4096000
TOTAL memory	24M * 4 bytes ~= 93MB / image (only forward! ~*2 for bwd)
TOTAL params	138M parameters

第一列是vgg16的网络结构，第二列是网络的feature map 以【高*宽*通道的形式展示出】第四列是参数，其中以参数的第一层为例子，卷积核是3*3*3然后有64个卷积核得到3*3*64个feature map  ，第一层的第二个卷积每个卷积核是3*3*64 有64个卷积核。依次往下计算。

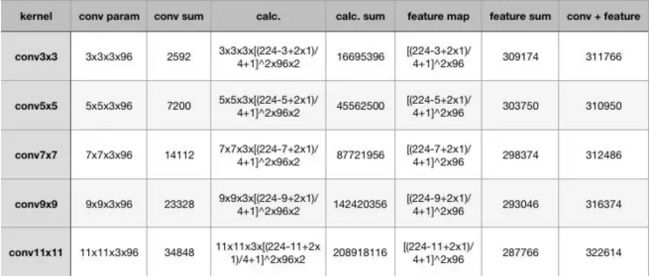
计算量：

    .                

1⃣️首先w2是卷积后的feature  map的长度，  w1是卷积前的feature map长度，  f是卷积核的长度，p是padding的长度，s是步长

             w2=(w1-f+2*p)/s+1   又因为卷积操作w1和w2的大小一样 可得   p=((w-1)*s-w+f)/2

2⃣️计算的都是一张3通道的图片 3*3*3的卷积核 w2为（224-3+2*1）/4+1   计算了整个图片的大小，所以是平方，有96个核所以便可得出上面的公式，可以看到参数量变化不大但是计算量是恐怖的。

其他

name / variable_scope 的使用：点击打开链接