Mr Ma

【论文翻译】Towards Robust Detection of Adversarial Examples

对抗样本的鲁棒检测

Towards Robust Detection of Adversarial Examples

Tianyu Pang, Chao Du, Yinpeng Dong, Jun Zhu

对抗样本的鲁棒检测

Towards Robust Detection of Adversarial Examples

摘要

1、介绍

2、准备工作Preliminaries

2.1符号

2.2威胁模型

2.3攻击方法

3、方法Methodology

3.1非最大熵Non-maximal entropy

3.2反向交叉熵训练程序

3.3阈值测试策略

4、实验

4.1设置

4.2对正常样本的分类器

4.3 oblivious攻击下的性能

4.4白盒攻击下的性能

4.5黑盒攻击下的性能

5、结论

附录A

摘要

虽然深度学习最近的进展是实质性的，但是深度学习方法容易受到恶意生成的对抗样本的攻击。在本文中，我们提出了一种新的训练方法和阈值测试策略，用于对抗样本的鲁棒检测。在训练中，我们建议最小化反向交叉熵(RCE, reverse cross entropy)，它鼓励深度网络学习潜在的表征(representations)，从而更好地区分对抗样本和正常样本。在测试中，我们建议使用阈值策略作为检测器来过滤掉对抗样本以获得可靠的预测。我们的方法使用标准算法实现简单，与普通的交叉熵最小化相比，几乎没有额外的训练成本。我们应用我们的方法来防御广泛使用的MNIST和CIFAR-10数据集上的各种攻击方法，并在对抗环境中的所有威胁方法下显著提升了预测的鲁棒性。

1、介绍

深度学习(DL)在各种任务中取得了前所未有的进展，包括图像分类、语音识别和自然语言处理[11]。然而，在对抗性环境中[12,33]，高精度的DL模型可能是脆弱的，在这种环境中，对抗样本被恶意生成，以误导模型输出错误的预测。现在已经开发了几种攻击方法来制造这样的对抗样本[2,4,12,18,22,29,30]。随着DL变得越来越普遍，提高鲁棒性是非常必要的，尤其是在安全关键型应用(safety-critical applications)中。

因此，已经提出了各种各样的防御，试图对对抗样本[14,25,31,32,33,36]进行正确分类。然而，这些防御措施大多不够有效，可能会被更强大的对手[2,3]成功攻击。在验证和训练可证明鲁棒网络[5,6,35]方面也有新的工作(There is also new work on verification and training provably robust networks)，但是这些方法只能提供逐点保证，并且它们需要大量额外的计算成本。总的来说，由于对抗样本甚至存在于简单的分类任务[9]和人眼[7]，这种方法不太可能通过防止对手产生对抗样本来解决问题。

由于困难，最近基于检测的防御作为替代解决方案吸引了很多注意。Grosse等人[13]在分类器中引入了一个额外的类，仅用于对抗样本，同样Gong等人[10]训练了一个额外的二元分类器来决定一个样本是否为对抗的。Metzen等人 [26]通过训练一个检测神经网络来检测对抗样本，该网络从分类网络的中间层获取输入。Bhagoji等人[1]降低输入到分类网络的输入图像的维数，并在较小的输入上训练全连接神经网络。Li和Li [21]建立级联分类器，其中每个分类器被实现为线性SVM，其作用于分类网络的内部卷积层的PCA。然而，这些方法都需要大量额外的计算成本，其中一些方法还会导致正常样本的准确性损失。相比之下，Feinman等人 [8]提出了一种核密度估计方法(kernel density estimate method)来检测位于最终层隐藏空间中远离数据流形(data manifolds)的点，这种方法不改变分类网络的结构，计算成本很小。然而，Carlini和Wagner [3]表明，这些防御方法中的每一种都可以被以特定防御为目标的对手回避，即白盒对手。

本文提出了一种防御方法，包括一种新的训练过程和阈值测试策略。阈值测试策略由[8]中引入的K-density (kernel density)检测器实现。在训练中，我们提出了一个新的称为反向交叉熵(RCE)的训练目标函数，来代替一般的交叉熵(CE)损失 [11]。通过最小化RCE，我们的训练过程鼓励分类器返回真实类的高置信度，同时对于每个数据点返回错误类的均匀分布，并且进一步使得分类器将正常样本映射到最后层隐藏空间中的低维流形(low-dimensional manifolds)的邻域。与CE相比，当使用K-density检测器或其他基于维度的检测器时，RCE训练过程可以学习更多关于过滤对抗样本的可区分表示(the RCE training procedure can learn more distinguishable representations on filtering adversarial examples)。与CE相比，使用随机梯度下降方法实现RCE最小化很简单，几乎没有额外的训练成本。因此，它可以很容易地应用于任何深度网络，并且与CE训练过程一样可扩展(scalable)。

我们使用我们的方法来防御被广泛使用的MNIST [20]和CIFAR-10[17]数据集上的各种攻击方法。我们在不同的威胁模型下测试我们方法的性能，即未察觉的对手(Oblivious adversaries)、白盒对手和黑盒对手。我们选择K-density估计方法作为我们的强基线，这显示了与其它基于探测的防御相比，其具有优越性和通用性[3]。结果表明，与基线相比，该方法提高了在所有威胁模型(models方法)下对抗敌对攻击(against adversarial attacks)的鲁棒性，同时在正常样本下保持了最先进的准确性。具体来说，我们显示出白盒对手必须用肉眼可见的噪声来精心制作对抗样本，才能成功规避我们的防御，这意味着人类观察者可以轻松过滤掉这些精心制作的对抗样本。

2、准备工作Preliminaries

本节提供符号并介绍威胁模型和攻击方法。

2.1符号

深度神经网络(DNN)分类器一般可以表示为一个映射函数 $F(X,\theta ):R^{d}\rightarrow R^{L}$ ，其中 $X\in R^{d}$ 是输入变量， $\theta$ 表示所有的参数，是类的数量(此后我们省略将 $\theta$ 为 $S(z)_{i}=\frac{exp(z_{i})}{\sum_{i=l}^{L} exp(z_{i})}$ ， $i\in [L]$ ，其中 $[L]:=\left \{ 1,...,L \right \}$ 。令为倒数第二层的输出向量，即最后一个隐藏层。这定义了一个映射函数 $X \mapsto Z$ 来提取数据表示。然后，分类器可以表示为 $F(X)=S(W_{s}Z+b_{s})$ ，其中 $W_{s}$ 和 $b_{s}$ 分别为softmax层的权重矩阵和偏置向量。我们将pre-softmax的输出 $W_{s}Z+b_{s}$ 表示为 $Z_{pre}$ ，称为logits。给定一个输入(即的一个实例)，预测标签为 $\widehat{y}=argmax_{i\in [L]}F(x)_{i}$ 。概率值 $F(x)_{i}$ 常被用作预测的置信度评分[11]。常见的训练目标是最小化交叉熵(cross-entropy, CE)损失，对一个单个输入-标签对，CE损失定义为: $L_{CE}(x,y)=-1_{y}^{\top }logF(x)=-logF(x)_{y}$ 。

其中 $1_{y}$ 是的one-hot编码，向量的对数定义为取每个元素的对数。CE训练程序旨在最小化训练数据的平均CE损失(在适当的正则化下)，以获得最佳参数。

2.2威胁模型

在敌对环境下，[3]引入了一个详细的威胁模型分类：

未察觉的对手(Oblivious adversaries)不知道检测器D的存在，并基于不安全的分类模型F生成对抗样本。
白盒对手知道D的方案和参数，可以设计特殊的方法同时攻击F模型和D检测器。
黑盒对手知道探测器D及其方案的存在，但无法获得探测器D或F模型的参数。

2.3攻击方法

虽然DNNs已经取得了长足的进步，但仍然可以很容易地识别出对抗样本来欺骗网络，甚至有时其有高的准确性[28]。近年来，提出了许多用来生成对抗样本的攻击方法。多数方法可以设计出在视觉上与正常样本难以区分，但被目标模型F错误分类的对抗样本。下面我们介绍一些众所周知且常用的攻击方法。

快速梯度符号法(Fast Gradient Sign Method, FGSM)：Goodfellow等人[12]介绍了一种一步攻击方法，该方法将对抗样本 $x^{\ast }$ 设计为 $x^{\ast }=x+\varepsilon \cdot sign(\triangledown _{x}L(x,y))$ ，其中 $\varepsilon$ 为扰动，为训练损失。

基本迭代法(Basic Iterative Method, BIM)：Kurakin等人[18]提出FGSM的迭代版本,公式为 $x_{i}^{\ast }=clip_{x,\varepsilon }(x_{i-1}^{\ast }+\frac{\varepsilon }{r}\cdot sign(\triangledown _{x_{i-1}^{\ast }}L(x_{i-1}^{\ast },y)))$ ，其中 $x_{0}^{\ast }=x$ ,为迭代步数， $clip_{x,\varepsilon }(\cdot )$ 是保持 $x_{i}^{\ast }$ 在其域内的剪切函数。

迭代最不可能类方法(Iterative Least-likely Class Method, ILCM)：Kurakin等人[18]也提出一个BIM的目标版本 $x_{i}^{\ast }=clip_{x,\varepsilon }(x_{i-1}^{\ast }-\frac{\varepsilon }{r}\cdot sign(\triangledown _{x_{i-1}^{\ast }}L(x_{i-1}^{\ast },y_{ll})))$ ，其中 $x_{0}^{\ast }=x$ ， $y_{ll}=argmin_{i}F(x)_{i}$ 。ILCM可以避免标签泄漏（label leaking）[19]，因为它不利用正确标签的信息。

基于jacobian的显著性映射攻击(Jacobian-based Saliency Map Attack, JSMA)：Papernot等人[30]提出了另一种针对目标攻击的迭代方法，该方法在每个迭代步骤中通过一个恒定的偏移量 $\varepsilon$ 来扰动一个特征，使下式显著性映射最大化

$S(x,t)[i]=\left\{\begin{matrix} 0,if\frac{\partial F(x)_{y}}{\partial x_{i}}<0 or \sum _{j\neq y}\frac{\partial F(x)_{j}}{\partial x_{i}}>0,\\ \left ( \frac{\partial F(x)_y}{\partial x_i} \right )\left | \sum _{j\neq y} \frac{\partial F(x)_j}{\partial x_i}\right |,otherwise \end{matrix}\right.$

与其他方法相比，JSMA扰动的像素更少。

Carlini &Wagner (C&W)：Carlini和Wagner[2]引入了一种基于优化的方法，这是最强大的攻击之一。他们用辅助变量 $\omega$ 定义了 $x^{\ast }=\frac{1}{2}(tanh(\omega )+1)$ ，并求出了问题 $min_{\omega }\left \| \frac{1}{2} (tanh(\omega )+1)-x\right \|_{2}^{2}+c\cdot f(\frac{1}{2}(tanh(\omega )+1))$ ,其中是一个常数,需要通过修改的二进制搜索（modified binary search）选择。 $f(\cdot )$ 是作为 $f(x)=max(max\left \{ Z_{pre}(x)_{i}:i\neq y \right \}-Z_{pre}(x)_{i},k)$ 的一个目标函数，其中控制置信度。

3、方法Methodology

在本节中，我们提出了一种新的方法来提高分类器在对抗设置下的鲁棒性。我们首先构造了一个新的度量指标，并对其性质进行了分析，从而得到了新的方法。

3.1非最大熵Non-maximal entropy

由于很难正确分类出对抗样本[2,3]且其普遍存在 [7,9]，我们设计了一种检测对抗样本的方法，这将有助于实际应用。例如，在半自动系统中，对抗样本的检测将允许禁用自动操作并请求人工干预[26]。

一个检测方法依赖于一些度量指标来决定对于给定的分类器，输入是否为对抗的。一个潜在的候选者是预测标签 $\hat{y}$ 上的置信度 $F(x)_{\hat{y}}$ ，其先天地传达了预测的确定性程度，并被广泛应用[11]。然而，先前的研究表明，在对抗背景下，置信度得分是不可靠的[12，28]。因此，我们构建了另一个与我们的目标更相关且更有帮助的指标。也就是说，我们定义了指标non-ME——中归一化的非最大元素的熵,为：

$non-ME(x)=-\sum _{i\neq \hat{y}}\hat{F}(x)_{i}log(\hat{F}(x)_{i})$ （1）

其中 $\hat{F}(x)_{i}=\frac{F(x)_{i}}{\sum _{j\neq \hat{y}}F(x)_{j}}$ 是中归一化的非最大元素。此后，我们将考虑给定，的最后一层隐藏向量，并在没有歧义情况下使用与含义相同的符号。为了直观地说明这些想法，图1a给出了隐藏空间中分类器的例子，其中 $z\in R^{2}$ 和。令 $Z_{pre,j}$ ， $i\in [L]$ 是logits $Z_{pre}$ 的第个元素。那么每对类和类之间的决策边界(decision boundary)就是超平面 $db_{ij}=\left \{ z:Z_{pre,i}=Z_{pre,j} \right \}$ ，并令 $DB_{ij}=\left \{ Z_{pre,i}=Z_{pre,j}+C,C\in R \right \}$ 是所有与 $db_{ij}$ 超平面平行的集合。在图1a中，每个 $db_{ij}$ 对应于三条黑线之一。我们表示半空间 $Z_{pre,i}\geq Z_{pre,j}$ 为 $db_{ij}^{+}$ 。然后，我们可以将 $\hat{y}$ 类的决策区域正式表示为 $dd_{\hat{y}}=\bigcap _{i,j\neq \hat{y}}db_{\hat{y}i}^{+}$ ，并将该区域的相应决策边界表示为 $\overline{dd_{\hat{y}}}$ 。注意，对于低维流形(the low-dimensional manifold） $S_{\hat{y}}=(\bigcap _{i,j\neq \hat{y}}db_{ij})dd_{\hat{y}}$ 上的任意点，输出具有个相等的非最大元素。运用上面的符号，我们有如下引理1：

引理1(证明于附录A)在 $\hat{y}$ 类决策区域 $dd_{\hat{y}}$ 内， $\forall i,j\neq \hat{y},\widetilde{db_{ij}}\in DB_{ij}$ ,在低维流形 $\bigcap _{i,j\neq \hat{y} }\widetilde{db_{ij}}$ 上任意点的non-ME值是常数。特别的，non-ME有且仅在 $S_{\hat{y}}$ 下获得全局最大值。

引理1告诉我们，在 $\hat{y}$ 类的决策区域内，如果一个沿着低维流形 $\bigcap _{i,j\neq \hat{y} }\widetilde{db_{ij}}$ 移动一个正常输入，那么它的non-ME值就不会改变，反之亦然。

定理1(证明于附录A)在 $\hat{y}$ 类决策区域 $dd_{\hat{y}}$ 内， $\forall i,j\neq \hat{y},z_{0}\in dd_{\hat{y}}$ ，存在一个独特的 $\widetilde{db_{ij}^{o}}\in DB_{ij}$ ，使得 $z_{0}\in Q_{0}$ ，其中 $Q_{0}=\bigcap _{i,j\neq \hat{y}}\widetilde{db_{ij}^{o}}$ 。令 $Q_{0}^{\hat{y}}=Q_{0}\bigcap \overline{dd_{\hat{y}}}$ ,那么问题

$\underset{z_{0}}{argmin}(\underset{z\in Q_{0}^{\hat{y}}}{max}F(z)_{\hat{y}})$

的解集是 $S_{\hat{y}}$ 。此外， $\forall z_{0}\in S_{\hat{y}}$ 有 $Q_{0}=S_{\hat{y}}$ ，且 $\forall z\in S_{\hat{y}}\bigcap \overline{dd_{\hat{y}}}$ ， $F(z)_{\hat{y}}=\frac{1}{L}$ 。

令 $z_{0}$ 表示为预测类 $\hat{y}$ 的一个正常样本。当基于 $z_{0}$ 构造对抗样本时，对手需要扰动 $z_{0}$ 去跨越决策边界 $\overline{dd_{\hat{y}}}$ 。定理1表示，存在一个独特的(unique)低维流形 $Q_{0}$ ， $z_{0}$ 位于类 $\hat{y}$ 的决策区域。如果我们能够以某种方式，在对手扰动 $z_{0}$ 时限制他们改变non-ME的值，那么通过引理1，对手只能沿着流形 $Q_{0}$ 扰动 $z_{0}$ 。在这种情况下， $z_{0}$ 最接近的扰动对应者（the nearest adversarial counterpart） $z^{\ast }$ 必须在 $Q_{0}^{\hat{y}}$ 集中[27]。那么 $\underset{z\in Q_{0}^{\hat{y}}}{max}F(z)_{\hat{y}}$ 的值是预测置信度 $F(z^{\ast })_{\hat{y}}$ 的上界。这个上界是 $z_{0}$ 的一个函数。定理1进一步告诉我们，如果 $z_{0}\in S_{\hat y}$ ，上界的相应值将获得它的最小值 $\frac{1}{L}$ ，这导致 $F(z^{\ast })_{\hat{y}}=\frac{1}{L}$ 。这使得 $z^{\ast }$ 很容易被区分，因为它的置信度得分低。

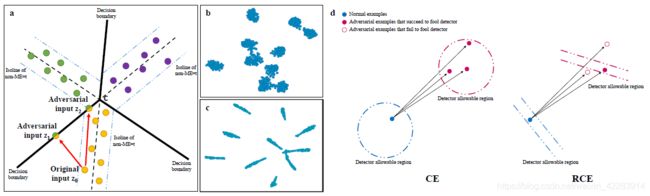【论文翻译】Towards Robust Detection of Adversarial Examples_第1张图片

图1: a，三条黑色实线是分类器的决策边界，每条黑线(实线和虚线部分)是两个类之间的决策边界。蓝色点划线是non-ME=t的等值线。b，t-SNE CIFAR-10上最终隐藏向量的可视化。模型是Resnet-32。训练程序是CE。c，训练程序是RCE。d，对训练好的网络的实际攻击。蓝色区域是正常样本的原始类别，红色区域是对抗样本的目标类别。

实际上，这种限制可以通过带有non-ME度量的检测器来实现。在图1a的情况下，位于集合 $S_{\hat{y}}$ (黑色虚线)上的任何点都具有最高的值。假设学习到的representation转换： $X \mapsto Z$ 可以将所有正常样本映射到 $S_{\hat{y}}$ 的邻域，其中邻域边界由 (蓝色点划线)的等值线（isolines）组成。这意味着所有正常样本的non-ME值都。当没有检测器时，基于 $z_{0}$ 的最近对抗样本是 $z_{1}$ ，其位于关于 $z_{0}$ 最近的决策边界上。相反，当使用non-ME作为检测度量时， $z_{1}$ 将很容易被检测器滤除，因为 $non-ME(z_{1})<t$ ，并且在这种情况下，最近的对抗样本变成 $z_{2}$ ，其位于邻域边界和决策边界的连接流形上。很容易得出结论：几乎每个地方， $\left \| z_{0}-z_{2} \right \|>\left \|z_{0}-z_{1} \right \|$ 。这意味着，由于检测器的存在，对手必须施加更大的最小扰动，才能成功地产生可以欺骗检测器的对抗样本。此外，根据定理1， $z_{2}$ 处的置信度也低于 $z_{1}$ 处的置信度，这使得 $z_{2}$ 仍然最有可能被区分，因为它的置信度得分低。

3.2反向交叉熵训练程序

基于以上分析，我们现在设计一个新的训练目标来提高DNN分类器的鲁棒性。关键是执行DNN分类器，将所有正常样本映射到最后一层隐藏空间中的低维流形 $S_{\hat{y}}$ 的邻域。根据引理1，这可以通过使的非最大元素尽可能相等来实现，因此对于每个正常输入具有一个高的non-ME值。具体来说，对于一个训练数据，我们令 $R_{y}$ 表示它的反向标签向量， $R_{y}$ 的第个元素为零，其他元素等于 $\frac{1}{L-1}$ 。实现的非最大元素之间一致性的一个明显方法是应用称为标签平滑（label smoothing）[34]的模型正则化方法，其可以通过在CE目标中引入 $R_{y}$ 和之间的交叉熵项来实现：

$L_{CE}^{\lambda }=L_{CE}(x,y)-\lambda \cdot R_{y}^{\top }logF(x)$ ，（2）

其中 $\lambda$ 是一个权衡参数。然而，很容易证明最小化 $L_{CE}^{\lambda }$ 等价于最小化和维向量 $P^{\lambda }$ 之间的交叉熵，其中

$P_{i}^{\lambda }=\left\{\begin{matrix} \frac{1}{\lambda +1}, i=y\\ \frac{\lambda }{(L-1)(\lambda +1)},i\neq y \end{matrix}\right.$ （3）

请注意， $1_{y}=P^{0}$ 和 $R_{y}=P^{\infty }$ 。当 $\lambda >0$ 时，令 $\theta _{\lambda }^{\ast }=argmin_{\theta }L_{CE}^{\lambda }$ ，那么预测 $F(x,\theta _{\lambda }^{\ast })$ 将倾向等于 $P^{\lambda }$ ，而不是真值 $1_{y}$ 。这使得输出预测有偏差。为了得到无偏差的预测，使输出向量趋向于 $1_{y}$ ，同时鼓励非正确（untrue）类上概率的一致性，我们定义了另一个基于名为反向交叉熵(reverse cross-entropy, RCE)的目标函数为

$L_{CE}^{R}(x,y)=-R_{y}^{\top }logF(x)$ 。（4）

最小化RCE相当于最小化 $L_{CE}^{\infty }$ 。注意，通过直接最小化 $L_{CE}^{R}$ ，即 $\theta _{R}^{\ast }=argmin_{\theta }L_{CE}^{R}$ ，可以得到一个反向分类器 $F(x,\theta _{R}^{\ast })$ ，这意味着给定输入，反向分类器 $F(x,\theta _{R}^{\ast })$ 不仅倾向于将最低概率分配给正确(true）类，而且倾向于在其他类上输出均匀分布。这一简单的见解引出了我们整个RCE训练程序，该程序由两部分组成，如下所述：

反向训练：给定训练集 $D:=\left \{ (x^{i},y^{i}) \right \}_{i \in[N]}$ ，通过最小化平均RCE损失来训练DNN $F(X,\theta )$ 成为反向分类器。最小化平均RCE损失： $\theta _{R}^{\ast }=argmin_{\theta }\frac{1}{N}\sum_{i=1}^{N}L_{CE}^{R}(x^{i},y^{i})$ 。

反向logits：最后的logits的负数输入到softmax层为 $F_{R}(X,\theta _{R}^{\ast })=S(-Z_{pre}(X,\theta _{R}^{\ast }))$ (Negating the final logits fed to the softmax layer as $F_{R}(X,\theta _{R}^{\ast })=S(-Z_{pre}(X,\theta _{R}^{\ast }))$ )。然后我们将获得网络 $F_{R}(X,\theta _{R}^{\ast })$ ,它返回关于类的普通预测， $F_{R}(X,\theta _{R}^{\ast })$ 被称为通过RCE训练程序训练的网络。

定理2(证明于附录A)假设是给定的训练数据。在 $L_{\infty }$ 范数下，如果存在训练误差 $\alpha \ll \frac{1}{L}$ 即 $\left \| S(Z_{pre}(x,\theta _{R}^{\ast }))-R_{y} \right \|_{\infty }\leq \alpha$ ，那么我们有边界

$\left \| S(-Z_{pre}(x,\theta _{R}^{\ast }))-1_{y} \right \|_{\infty }\leq \alpha (L-1)^{2}$ ，

和 $\forall j,k\neq y$ ,

$\left | S(-Z_{pre}(x,\theta _{R}^{\ast }))_{j}- S(-Z_{pre}(x,\theta _{R}^{\ast }))_{k}\right |\leq 2\alpha ^{2}(L-1)^{2}$ 。

定理2展示了RCE训练过程的两个重要性质。首先，一致和公正的是当训练误差 $\alpha \rightarrow 0$ 时，输出 $F_{R}(X,\theta _{R}^{\ast })$ 收敛到one-hot标签向量 $1_{y}$ 。第二，输出中任何两个非最大元素之间的差值的上界随着关于 $\alpha$ 的 $O(\alpha ^{2})$ 减小，比 $O(\alpha )$ 和标签平滑更快。这两个属性使RCE训练程序符合我们的上述要求。

3.3阈值测试策略

给定一个已训练的分类器，我们通过一个检测器来实现阈值测试策略，用于鲁棒预测。预设度量后，如果度量值大于阈值T，则检测器将输入分类为正常，并决定返回预测标签；或者在其他情况下，将输入分类为敌对的，返回“不确定”。在我们的方法中，我们采用了[8]中引入的核密度(Kernel density, K-density)度量，因为将K-density度量应用于CE训练已经显示出比其他防御系统[3]更好的鲁棒性和通用性。K-density可以被认为是置信度和non-ME度量的某种组合，因为它可以同时传递关于它们的信息。

Kernel density：K-density是在最后一层隐藏空间中计算的。给定预测标签 $\hat{y}$ ，K-density定义为 $KD(x)=\frac{1}{\left | X_{\hat{y}} \right |}\sum _{x_{i}\in X_{\hat{y}}}k(z_{i},z)$ ，其中 $X_\hat{y}$ 代表具有标签 $\hat{y}$ 的训练点集，和是相应的最后一层隐藏向量， $k(z_{i},z)=exp(-\frac{\left \| z_{i}-z \right \|^{2}}{\sigma ^{2}})$ 是高斯核，带宽（bandwidth） $\sigma$ 被视为超参数。

Carlini和Wagner[3]表明，以前检测对抗样本的方法可以被白盒对手回避。然而，我们的方法(RCE训练+ K-density检测器)可以有效地防御白盒攻击。这是因为RCE训练过程隐藏了最后一层隐藏空间中的低维流形上的正常样本，如图1b和图1c所示。那么检测器允许的区域也可以被设置为低维的，只要这些区域包含所有正常样本。因此，那些想欺骗我们检测器的白盒对手必须用更精确的计算和更大的噪声来产生对抗样本。这在图1d中直观显示，其中在由CE训练的网络上制作的对抗样本比在由RCE训练的网络上制作的对抗样本更容易位于检测器允许的区域中。这在第4.4节中得到实验验证。

4、实验

我们现在给出实验结果来证明我们的方法在对抗环境中提高DNN分类器鲁棒性的有效性。

4.1设置

我们使用了两个广泛研究的数据集——MNIST[20]和CIFAR-10[17]。MNIST是手写数字的集合，训练集有6万幅图像，测试集有1万幅图像。CIFAR-10由10个类别的6万幅彩色图像组成，每个类别有6千幅图像。其中5万个训练图像和1万个测试图像。两个数据集中图像的像素值被缩放到区间。我们实验中的正常样本指的是训练和测试集中的所有样本。在对抗环境中，我们使用的强基线（strong baseline）是K-density估计方法(CE训练 + K-density检测器)[8]，与其他在[3]中基于检测的防御方法[1,10,13,21,26]相比，该方法显示了其优越性和通用性。

4.2对正常样本的分类器

我们首先在正常设置下进行评估，Resnet-32和Resnet-56 [15]模型都对以上两个数据集实现。对于每一个网络，我们都使用CE和RCE作为训练目标，与He等人[16]相同的设置进行训练。这两个目标的训练步(training steps)的个数在MNIST定为20000个，在CIFAR-10定为90000个。为了便于表示，我们将在已训练网络的模型名称后指出所使用的训练程序，例如Resnet-32 (CE)。类似地，我们在攻击方法之后指示训练程序，且省略目标网络的名称，例如FGSM(CE)。表1显示了测试错误率，其中阈值测试策略被禁用，并且所有点都接收它们的预测标签(all the points receive their predicted labels)。我们可以看到，RCE训练的网络的表现与传统的CE程序训练的网络一样好，有时甚至更好。请注意，我们在CE和RCE程序上都应用相同的训练超参数(例如，学习率和衰减因子)，这表明RCE易于优化，并且不需要在调整超参数上做太多额外的工作。

【论文翻译】Towards Robust Detection of Adversarial Examples_第2张图片

表1：测试集上的分类错误率(%)

为了验证RCE过程倾向于将所有正常输入映射到隐藏空间中的 $S_{\hat{y}}$ 邻域，我们应用t-SNE技术[24]来可视化测试集上最后隐藏层向量的分布。图1b和图1c给出了1000个CIFAR-10测试样本的二维可视化结果。我们可以看到，由RCE训练的网络可以成功地将测试实例映射到最后一层隐藏空间中的低维流形的邻域。

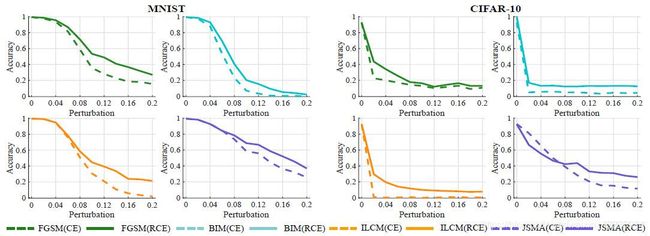
4.3 oblivious攻击下的性能

我们测试了MNIST和CIFAR-10上经过训练的Resnet-32网络在oblivious攻击下的性能，其中我们研究了在2.3节中的攻击方法。我们首先禁用阈值测试策略，并让分类器返回所有预测，以研究网络正确分类对抗样本的能力。我们使用了基于迭代的攻击方法：FGSM、BIM、ILCM和JSMA，并计算了网络关于扰动 $\varepsilon$ 在精心制作的对抗样本上的分类精度(calculate the classification accuracy of networks on crafted adversarial examples w.r.t. the perturbation $\varepsilon$ )。图2a展示了结果。我们可以看到，在对两个数据集的所有四种攻击下，Resnet-32 (RCE)比Resnet-32 (CE)具有更高的准确度分数。

【论文翻译】Towards Robust Detection of Adversarial Examples_第3张图片

(a) 基于迭代攻击下的分类精度

【论文翻译】Towards Robust Detection of Adversarial Examples_第4张图片

(b) 平均最小失真
图2：禁用阈值测试策略的鲁棒性。目标网络的模型是Resnet-32。

至于基于优化的方法，如C&W攻击及其变种，我们采用与[3]中相同的方法来报告鲁棒性。具体来说，我们对参数进行二进制（二元）搜索，以便找到能够成功攻击分类器的最小失真。该失真在[33]中被定义为 $\left \| x-x^{\ast } \right \|_{2}/\sqrt{d}$ ，其中 $x^{\ast }$ 是生成的对抗样本，并且每个像素特征被重新缩放到[0, 255]。我们将C&W攻击的步长设置为0.01，并将的二进制搜索轮数设置为9，每轮最大迭代步长为10000。此外，为了使我们的研究更有说服力，我们引入了C&W攻击的高置信度版本(缩写为C&W-hc ),该版本在我们的实验中将C&W攻击中的参数设置为10。C&W-hc攻击可以产生置信度高于0.99的对抗样本，并且先前的工作表明，C&W-hc制作的对抗样本比C&W[2,3]制作的更强，更难防御。结果如图2b所示。我们可以看到，C&W和C&W-hc攻击需要比CE训练的网络更大的最小失真来成功攻击RCE训练的网络。在白盒攻击下也观察到类似的现象。

我们进一步使用K-density度量来激活阈值测试策略，并且还测试置信度或non-ME的性能以进行更完整地分析。我们构造简单的二元分类器，通过度量阈值来判断一个样本是否为敌对的，然后在这些二元分类器上计算ROC曲线的AUC分数。表2显示了在两个数据集上训练程序和阈值度量的不同组合下计算的AUC分数。从表2中，我们可以看到我们的方法(RCE训练+ K-density检测器)几乎在所有情况下都表现最好，而non-ME本身也是一个相当可靠的度量，尽管不如K-density好。RCE训练的分类器也返回了更可靠的置信度得分，验证了定理1的结论。此外，我们还表明，我们的方法可以更好地区分噪声样本(noisy examples)和对抗样本，如附录B.3所示。

【论文翻译】Towards Robust Detection of Adversarial Examples_第5张图片

表2:对抗样本的AUC分数(10^-2)。目标网络的模型是Resnet-32。值根据正确分类为普通样本的样本计算,然后误分类为对抗样本。计算K-density时使用的带宽为 CE带宽的平方=1/0.26和 RCE带宽的平方=0.1/0.26。此处 (-)表示强基线,(*)指示我们的防御方法。

4.4白盒攻击下的性能

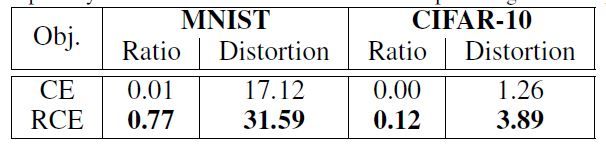
我们在白盒攻击下测试我们的方法，这是最困难的威胁模型，目前还没有有效的防御手段。我们应用了[3]中引入的C&W攻击的白盒版本(缩写为C&W-wb)，它是专门用来愚弄K-density检测器的。C&W-wb也是我们方法的白盒攻击，因为它没有利用训练目标的信息。C&W-wb引入了一个新的损失术语 $f_{2}(x^{\ast })=max(-log(KD(x^{\ast }))-\eta ,0)$ 这惩罚了由K-density检测器检测到的对抗样本 $x^{\ast }$ ，其中 $\eta$ 被设置为 $-log(KD(\cdot ))$ 的中值。表3显示了C&W-wb制作的对抗样本中的平均最小失真以及 $f_{2}(x^{\ast })>0$ 的比率，其中较高的比率表明检测器更鲁棒，更难被愚弄。我们发现，几乎所有在Resnet-32 (CE)上生成的对抗样本都具有 $f_{2}(x^{\ast })\leq 0$ ，这意味着它们的K-density值大于训练数据值的一半。这个结果与以前的工作[3]是一致的。

【论文翻译】Towards Robust Detection of Adversarial Examples_第6张图片

表3：f2(x*)>0的比例和C&W-wb制作的对抗样本的最小失真。模型是Resnet-32。

然而，请注意，在我们的方法中应用C&W-wb具有高得多的比率，并导致更大的最小失真。图3显示了一些与正常样本对应的由C&W-wb制作的对抗样本。我们发现Resnet-32 (CE)上制作的对抗样本与普通样本无法用肉眼区分。相比之下，在Resnet-32 (RCE)上制作的对抗样本具有肉眼可见的噪声，这并不是严格意义上的对抗样本，因为它们在视觉上区别于正常样本。在我们的防御下最具攻击性的C&W-wb的低效率验证了我们在图1d的阐述。更多关于C&W-wb局限的细节见附录B.4。我们还设计了利用RCE训练损失信息的白盒攻击，与C&W-wb相比，我们的攻击效率较低。这是因为给定一个输入，它的RCE值和K-density分数之间没有明确的关系。因此，像C&W-wb那样直接攻击K-density检测器更有效。

【论文翻译】Towards Robust Detection of Adversarial Examples_第7张图片

图 3：正常测试图像称为"Normal",在Resnet-32 (CE)和Resnet-32 (RCE)上生成的对抗样本分别称为 CE和RCE。对抗样本由最小失真的 C&W-wb 生成。

4.5黑盒攻击下的性能

为了进行完整的分析，我们研究了黑盒攻击下的鲁棒性。黑盒攻击的成功是基于不同型号之间对抗样本的可转移性[12]。我们将经过训练的Resnet-56网络设置为目标模型。对手打算攻击他们，但无法获得他们的参数。因此，我们将经过训练的Resnet-32网络设置为对手实际攻击的代理模型(substitute models)，然后将精心制作的对抗样本输入目标模型。由于对手知道K-density检测器的存在，我们采用了C&W-wb攻击。我们发现，C&W-wb攻击形成的对抗样本的可转移性较差，其中不到50%的对抗样本会使目标模型在MNIST错误分类，在CIFAR-10上不到15%。表4显示了针对CIFAR-10的黑箱攻击的四种不同情况下的AUC分数，而针对MNIST的相同情况下的AUC分数均高于95%。请注意，在我们的实验中，目标模型和代理模型具有非常相似的结构，即使在这种相当接近“白色”的黑盒攻击下，C&W-wb攻击也变得无效。

【论文翻译】Towards Robust Detection of Adversarial Examples_第8张图片

表4：CIFAR-10上的AUC分数(10^-2)。Resnet-32是代理模型,Resnet-56是目标模型。

5、结论

我们提出了一种新的方法，通过可靠地检测和过滤对抗样本来提高深度学习模型的鲁棒性，该方法可以使用标准算法来实现，而几乎没有额外的训练成本。在所有威胁模型和各种攻击方法下，我们的方法在MNIST和CIFAR-10数据集上都表现良好，同时保持了在正常样本上的准确性。

附录A

你可能感兴趣的:(论文翻译)

论文翻译：arxiv-2022 Ignore Previous Prompt: Attack Techniques For Language Models CSPhD-winston-杨帆论文翻译 LLMs-安全 prompt 语言模型人工智能
IgnorePreviousPrompt:AttackTechniquesForLanguageModelshttps://arxiv.org/pdf/2211.09527忽略之前的提示：针对语言模型的攻击技术文章目录忽略之前的提示：针对语言模型的攻击技术摘要1引言摘要基于Transformer的大型语言模型（LLMs）为大规模面向客户的应用程序中的自然语言任务提供了强大的基础。然而，探索恶意用户
论文翻译：arxiv-2024 Data Contamination Quiz: A Tool to Detect and Estimate Contamination in Large CSPhD-winston-杨帆 LLMs-数据污染论文翻译语言模型人工智能深度学习
DataContaminationQuiz:ATooltoDetectandEstimateContaminationinLargeLanguageModelshttps://arxiv.org/abs/2311.06233数据污染测验：一种检测和估计大型语言模型中污染的工具文章目录数据污染测验：一种检测和估计大型语言模型中污染的工具摘要1引言摘要我们提出了数据污染测验（DataContamina
实验DAY5：借假修真放逐997
a.昨日完成情况不佳，起床是9.30，除了报名（一口气报了五门..祝我好运），论文翻译和教育都没有完成；b.明日计划：9点前起床；明天优先复盘教育，以及准备cpa的考试资料；论文、和cpa留到周末做吧c.今天读到一篇讲美团公司战略的文章，对于整体战略搭建的方法论、具体业务的促成、以及更偏意识上层的“借假修真”思想的解读非常佩服，摘录核心如下：美团的增长引擎：1.严明的纪律性：放弃不符合业务逻辑的利
开源Bluespec bsc编译器和可重用示例设计达坦科技DatenLord 硬件加速 fpga fpga开发硬件工程开源
这篇介绍Bluespec以及设计示例的文章，是在2021年ICCAD（InternationalConferenceOnComputer-AidedDesign）发布的论文。达坦科技的open-rdma项目和推广的MIT体系结构学习社区都用到Bluespec，因此将此论文翻译成中文，以便大家了解2020年Bluespec开源后相关的开源项目。摘要：bsc编译器是一个商业可用的编译器，在过去的二十年
论文翻译 - BITE: Textual Backdoor Attacks with Iterative Trigger Injection anniewwy LLM Backdoor Attack
论文链接：https://arxiv.org/pdf/2205.12700.pdf项目代码：https://github.com/INK-USC/BITEBITE:TextualBackdoorAttackswithIterativeTriggerInjectionAbstract1Introduction2ThreatModel3Methodology3.1BiasMeasurementonLa
我做这件事，唯一的目的就是让你开心沉吟大叔
一个男人心里满满的爱意：我做这件事，唯一的目的就是让你高兴，而不是赢得你的好感、证明我的能力、让你对我感恩戴德。所以，我不想让你知道我的付出，不想让你对我怀有歉意和内疚，更不想因此获得什么回报。我只是心甘情愿地想为你做点什么，因为我爱你。这才是真爱吧。以前有个读者，说她男朋友特别小气，还不诚实。请她吃顿饭要念叨很久，给她买礼物，花一百要说成三百，帮她做论文翻译，明明一小时就搞定了，非要说是熬了个通
剖析以太坊上的庞氏骗局：识别、分析和影响卷神
区块链安全防护论文翻译：Bartoletti,Massimo,etal."DissectingPonzischemesonEthereum:identification,analysis,andimpact."FutureGenerationComputerSystems102(2020):259-277.摘要：庞氏骗局是一种以高额利润为诱饵的金融欺诈。实际上，只有新用户加入了庞氏骗局，用户才能得
《 HFContractFuzzer: Fuzzing Hyperledger Fabric Smart Contractsfor Vulnerability Detection》论文翻译 WXF_Security 智能合约安全研究 fabric golang
《HFContractFuzzer:FuzzingHyperledgerFabricSmartContractsforVulnerabilityDetection》（EASE2021）摘要区块链技术以其特有的去中心化、不可变性等优点，近年来被广泛应用于各个领域。运行在区块链上的智能合约在去中心化应用场景中也扮演着越来越重要的角色。因此，自动检测智能合约中的安全漏洞成为区块链技术应用中亟待解决的问题
Data Augmentation and Deep Learning Methods in SoundClassification: A Systematic Review ggqyh 深度学习人工智能
文章为翻译，仅供学习参考论文原地址：DataAugmentationandDeepLearningMethodsinSoundClassification:ASystematicReview作者：OlusolaO.Abayomi-Alli,RobertasDamaševiˇcius,AtikaQazi,MariamAdedoyin-OloweandSanjayMisra4论文翻译地址：https:
因果学习及反因果学习（论文翻译）三分钟湿度
OnCausalandAnti-causalLearning本博文对论文OnCausalandAnti-causalLearning的摘要和模型部分做了翻译和小修改，本论文主要描述因果学习中常见的几类基于函数估计的模型，同时说明了因果与相关性、因果学习与机器学习之间的关系，论文重点在讨论和比较不同模型，内容较为笼统，不做深入探讨，但对不同模型之间的本质关系的讨论值得一看。论文地址：https://
Convolutional Neural Networks for No-Reference Image Quality Assessment 论文翻译亚里论文阅读 NR-IQA 使用卷积网络进行图像质量评价
ConvolutionalNeuralNetworksforNo-ReferenceImageQualityAssessment论文翻译TranslationAbstract1Introduction2RelatedWork3CNNforNR-IQA3.1NetworkArchitecture3.2LocalNormalization3.3Pooling3.4ReLUNonlinearity3.5
有道论文翻译接口，python版和lua版 monsterskiller 手机编程脚本编程 python
论文翻译接口python版importrequestsimporthashlibfromurllib.parseimportquotedefget_md5(s,is_hex=True):md5=hashlib.md5()md5.update(s.encode())ifis_hex:returnmd5.hexdigest()returnmd5.digest()deftranslate(source_
医学论文翻译有哪些要求，应该如何翻译呢？英信翻译公司其他
近年来，随着国内医学水平的不断提高，医学论文翻译的需求也呈现出快速增长的趋势。在国外期刊上发表论文，往往需要将整篇论文翻译成英文。那么，医学论文翻译有哪些要求，应该如何翻译呢？专家指出，医学论文翻译最基本的要求就是准确性，要求翻译者能够准确地将原文的含义传达给读者，不出现歧义或者误解的情况。这要求翻译者具备深厚的医学专业知识和语言能力，能够理解原文的含义，并将其准确地表达出来。除了准确性之外，医学
GPT原始论文：Improving Language Understanding by Generative Pre-Training论文翻译 iKang_dlut gpt 人工智能深度学习
1摘要自然语理解包括文本蕴含、问题回答、语义相似性评估和文档分类等一系列多样化的任务。尽管大量未标注的文本语料库很丰富，但用于学习这些特定任务的标注数据却很稀缺，这使得基于区分性训练的模型难以充分发挥作用。我们展示了通过在多样化的未标注文本语料库上对语言模型进行生成式预训练，随后对每个特定任务进行区分性微调，可以实现这些任务的大幅度改进。与以往的方法不同，我们在微调过程中使用了任务感知的输入转换，
【论文翻译】Generation of Non-Deterministic Synthetic Face Datasets Guided by Identity Priors（21.12）联系丝信计算机视觉
文章目录读后感Abstract1Introduction1.1Ourcontributions2RelatedWorks2.1SyntheticImageGeneration2.2MatedSampleGeneration2.3LimitationsinState-of-the-art3PCA-FR-GuidedSampling4SyntheticMatedFace(SymFace)Dataset
ORB-SLAM2代码学习1 rgdb_tum.cc Dziwu SLAM 学习计算机视觉人工智能
论文翻译参考1参考2rgdb_tum.cc的框架代码大致思路LoadImages()加载图像——判断rgb图是否存在——判断rgb图与depth图数量是否对应相同。ORB_SLAM2::SystemSLAM()初始化，创建SLAM系统，并初始化各个线程。遍历每一对RGB图和depth图【读取RGB图和depth图，读取时间戳（vTimestamps存储了时间戳，实际上就是存储了数据文件的每一幅图像
GFS--Google File System论文翻译和理解不争_900c
一、系统设计目标高可用的大文件分布式文件系统。二、关键点Architecture-架构：有哪些Server，每个Server的功能。Master存储的MetaData的结构。client写数据流程。client读数据流程。启动时Master和ChunkServer的交互。ChunkServer发生故障时，Master和ChunkServer的交互。三、核心设计概述2.Master中存储的MetaD
翻译 5765f3fa240e
对于论文翻译，大家要极其重视阅读平行文本和查资料的重要性。我平时经常做论文翻译和润色，每一次都是如履薄冰。需要阅读核心参考文献，查资料消除术语，彻底领会论文背后的逻辑。这些都解决了，才轮到运用语言基本功。假如大家接论文翻译，请认真对待查资料和阅读平行文本这两件事，如果做不到，暂时不要接论文翻译。
BERT论文翻译 TheHonestBob NLP 自然语言处理
一、写在前面在Transformer和BERT大行其道的时代，搞懂这两种基础模型结构很有必要，在网上没有搜索到满意的论文翻译结果，最近刚好有时间，把BERT的论文在个人英语水平基础上最大程度的保留原作者的本意翻译一遍，如有翻译不到位的地方请各位指出，觉得不错的点个赞鼓励一下，Tansformer的论文我之前已经翻译了，可以查看我的这篇博客attentionisallyouneed论文翻译。查看be
ImageNet Classification with Deep Convolutional Neural Networks论文翻译——中英文对照 SnailTyan 深度学习 Deep Learnig
文章作者：Tyan博客：noahsnail.com|CSDN|简书翻译论文汇总：https://github.com/SnailTyan/deep-learning-papers-translationImageNetClassificationwithDeepConvolutionalNeuralNetworksAbstractWetrainedalarge,deepconvolutionaln
2021-02-05 碰撞检测GJK算法详解（初学者慎入） MathPhilosophy
碰撞检测有2个经典算法，一个是分离轴算法SAT,还有一个就是本文要介绍的GJK，GJK是三个人的名字首写大字母；这个算法的数学推导有点复杂，目前网上只有这篇https://blog.csdn.net/u010016421/article/details/104788769/相对比较详细的介绍了算法，其主要也是参考原始论文翻译的；考虑到原始论文比较难读，博主特地专门写一篇文章介绍，博主的这篇文章会必
YoloV8改进策略：BackBone改进|DCNv4最新实践|高效涨点|多种改进教程|完整论文翻译静静AI学堂 YOLO
摘要涨点效果：在我自己的数据集上，mAP50由0.986涨到了0.993，mAP50-95由0.737涨到0.77，涨点明显！DCNv4是可变形卷积的第四版，速度和v3相比有了大幅度的提升，但是环境搭建有一定的难度，对新手不太友好。如果在使用过程遇到编译的问题，请严格按照我写的环境配置。论文：《DCNv4：对视觉应用的动态和稀疏算子的重新思考》https://arxiv.org/pdf/2401.
论文翻译 SVSGAN: Singing Voice Separation Via Generative Adversarial Network 夏HL
文章主要是将混合音频的声谱作为输入，人声,bgm的声谱作为标签，通过GAN来完成近似过程，生成器最后一层用的output_voice=[z_voice/(z_voice+z_bgm)]*x,output_bgm=[z_bgm/(z_voice+z_bgm)]*x而且文章中的生成器是经过预先训练后的。我在MKR-100上用SVSGAN时难以训练(以后换成wgan)。0.摘要从混合音频中分离出两种来源
ALOHA论文翻译：Learning Fine-Grained Bimanual Manipulation with Low-Cost Hardware baidu_huihui 精细双手操作低成本硬件
学习用低成本硬件进行精细双手操作MobileALOHA论文翻译：LearningFine-GrainedBimanualManipulationwithLow-CostHardware论文翻译@[TOC]在这里插入图片描述图1：ALOHA：一种用于双手远程操作的低成本开源硬件系统。整个系统使用现成的机器人和3D打印组件，总成本不到20,000美元。左图：用户通过反向驱动领导机器人进行远程操作，从而
手把手教你用GPT写提示词；进行文献综述；论文翻译/润色及写作 asyxchenchong888 gpt4 GPT gpt chatgpt 人工智能 python
2023年随着OpenAI开发者大会的召开，最重磅更新当属GPTs，多模态API，未来自定义专属的GPT。微软创始人比尔盖茨称ChatGPT的出现有着重大历史意义，不亚于互联网和个人电脑的问世。360创始人周鸿祎认为未来各行各业如果不能搭上这班车，就有可能被淘汰在这个数字化时代，如何能高效地处理文本、文献查阅、PPT编辑、编程、绘图和论文写作已经成为您成功的关键。而ChatGPT，作为一种强大的自
【Linux系统下论文翻译软件Zotero】 Dymc 安装笔记 linux 服务器论文翻译软件
Linux系统下论文翻译软件Zotero1下载安装包2建立快捷方式3插件安装4翻译插件出现报错1下载安装包Linux系统下的论文翻译软件Zotero，下载地址：https://www.zotero.org/download/2建立快捷方式解压后，创建快捷方式，即创建软链接：sudomkdir/opt/zoterosudomvZotero_linux-x86_64/*/opt/zotero/cd/o
KGCapsAN论文翻译毕一
摘要：基于方面(方面级)的情感分析是在细粒度情感分析中非常重要的子任务，旨在自动推断出某一方面在其上下文中的情绪。之前的研究已经表明，利用注意力为基础的方法可以有效地提高基于方面的情感分析的精度。尽管有了卓越的进步,基于方面的情绪分析现实中几个方面挑战。(1)目前基于注意力的方法可能会导致某一方面的注意力不正确地集中在与句法无关的词上。(2)传统的方法无法将情感与特殊的句子结构区分开来，如双重否定
记你我的第一次相遇易美编校
Hi大家好！今天是易美编校在与你们的第一次相遇，让我想到了白落梅的《世间所有的相遇都是久别重逢》,人和人的缘分真的很深，可以维系千年，任凭风尘起落，情怀不改。人和人的缘分真的很浅，只不过是相逢刹那，转身便成了永远的陌路。不知道你我之间将会有怎样的一个开始？先做个自我介绍吧，Emate易美编校是北京龙华全科教育科技有限公司旗下学术服务品牌，旨在为非英语国家的科学家提供专业化的论文翻译、润色、修改及其
基于ChatGPT的代码解释神器：GPT Academic、GitHub Copilot 码上出奇迹 chatgpt gpt github
（个人推荐使用第二个GitHubCopilot）1.GPT学术优化(GPTAcademic)工具简介GPTAcademic是什么为ChatGPT/GLM提供实用化交互界面，特别优化论文阅读/润色/写作体验，模块化设计，支持自定义快捷按钮&函数插件，支持Python和C++等项目剖析&自译解功能，PDF/LaTex论文翻译&总结功能，支持并行问询多种LLM模型，支持chatglm2等本地模型。兼容文
推荐几个将pdf论文翻译转化为中文论文的免费在线网站 Wency(王斯-CUEB) 经验分享
如果你需要将英文PDF研究论文翻译成中文，有几个网站可以帮助你：OnlineDocTranslator【传送门】这项免费服务允许您上传PDF并将其翻译成中文。它支持包括PDF在内的多种文档格式，并保持文档的原始布局。GroupDocs【传送门】这个在线工具提供免费的PDF文档从英文到中文的翻译。它是一个基于浏览器的应用程序，因此不需要安装软件。请注意，PDF文档的字符限制为10,000个字符。Do
rust的指针作为函数返回值是直接传递，还是先销毁后创建？ wudixiaotie 返回值
这是我自己想到的问题，结果去知呼提问，还没等别人回答，我自己就想到方法实验了。。 fn main() { let mut a = 34; println!("a's addr:{:p}", &a); let p = &mut a; println!("p's addr:{:p}", &a
java编程思想 -- 数据的初始化百合不是茶 java 数据的初始化
1.使用构造器确保数据初始化 /* *在ReckInitDemo类中创建Reck的对象 */ public class ReckInitDemo { public static void main(String[] args) { //创建Reck对象 new Reck(); } }
[航天与宇宙]为什么发射和回收航天器有档期 comsci
地球的大气层中有一个时空屏蔽层,这个层次会不定时的出现,如果该时空屏蔽层出现,那么将导致外层空间进入的任何物体被摧毁,而从地面发射到太空的飞船也将被摧毁... 所以,航天发射和飞船回收都需要等待这个时空屏蔽层消失之后,再进行 &
linux下批量替换文件内容商人shang linux 替换
1、网络上现成的资料　　格式: sed -i "s/查找字段/替换字段/g" `grep 查找字段 -rl 路径` 　　linux sed 批量替换多个文件中的字符串　　sed -i "s/oldstring/newstring/g" `grep oldstring -rl yourdir` 　　例如：替换/home下所有文件中的www.admi
网页在线天气预报 oloz 天气预报
网页在线调用天气预报 <%@ page language="java" contentType="text/html; charset=utf-8" pageEncoding="utf-8"%> <!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.01 Transit
SpringMVC和Struts2比较杨白白 springMVC
1. 入口 spring mvc的入口是servlet，而struts2是filter（这里要指出，filter和servlet是不同的。以前认为filter是servlet的一种特殊），这样就导致了二者的机制不同，这里就牵涉到servlet和filter的区别了。参见：http://blog.csdn.net/zs15932616453/article/details/8832343 2
refuse copy, lazy girl! 小桔子 copy
妹妹坐船头啊啊啊啊！都打算一点点琢磨呢。文字编辑也写了基本功能了。。今天查资料，结果查到了人家写得完完整整的。我清楚的认识到： 1.那是我自己觉得写不出的高度 2.如果直接拿来用，很快就能解决问题 3.然后就是抄咩~~ 4.肿么可以这样子，都不想写了今儿个，留着作参考吧！拒绝大抄特抄，慢慢一点点写！
apache与php整合 aichenglong php apache web
一 apache web服务器 1 apeche web服务器的安装 1)下载Apache web服务器 2)配置域名(如果需要使用要在DNS上注册) 3)测试安装访问http://localhost/验证是否安装成功 2 apache管理 1)service.msc进行图形化管理 2)命令管理，配
Maven常用内置变量 AILIKES maven
Built-in properties ${basedir} represents the directory containing pom.xml ${version} equivalent to ${project.version} (deprecated: ${pom.version}) Pom/Project properties Al
java的类和对象百合不是茶 JAVA面向对象类对象
java中的类： java是面向对象的语言，解决问题的核心就是将问题看成是一个类，使用类来解决 java使用 class 类名来创建类，在Java中类名要求和构造方法，Java的文件名是一样的创建一个A类： class A{ } java中的类：将某两个事物有联系的属性包装在一个类中，再通
JS控制页面输入框为只读 bijian1013 JavaScript
在WEB应用开发当中，增、删除、改、查功能必不可少，为了减少以后维护的工作量，我们一般都只做一份页面，通过传入的参数控制其是新增、修改或者查看。而修改时需将待修改的信息从后台取到并显示出来，实际上就是查看的过程，唯一的区别是修改时，页面上所有的信息能修改，而查看页面上的信息不能修改。因此完全可以将其合并，但通过前端JS将查看页面的所有信息控制为只读，在信息量非常大时，就比较麻烦。
AngularJS与服务器交互 bijian1013 JavaScript AngularJS $http
对于AJAX应用（使用XMLHttpRequests）来说，向服务器发起请求的传统方式是：获取一个XMLHttpRequest对象的引用、发起请求、读取响应、检查状态码，最后处理服务端的响应。整个过程示例如下： var xmlhttp = new XMLHttpRequest(); xmlhttp.onreadystatechange
[Maven学习笔记八]Maven常用插件应用 bit1129 maven
常用插件及其用法位于：http://maven.apache.org/plugins/ 1. Jetty server plugin 2. Dependency copy plugin 3. Surefire Test plugin 4. Uber jar plugin 1. Jetty Pl
【Hive六】Hive用户自定义函数(UDF) bit1129 自定义函数
1. 什么是Hive UDF Hive是基于Hadoop中的MapReduce，提供HQL查询的数据仓库。Hive是一个很开放的系统，很多内容都支持用户定制，包括：文件格式：Text File，Sequence File 内存中的数据格式： Java Integer/String, Hadoop IntWritable/Text 用户提供的 map/reduce 脚本：不管什么
杀掉nginx进程后丢失nginx.pid，如何重新启动nginx ronin47 nginx 重启 pid丢失
nginx进程被意外关闭，使用nginx -s reload重启时报如下错误：nginx: [error] open() “/var/run/nginx.pid” failed (2: No such file or directory)这是因为nginx进程被杀死后pid丢失了，下一次再开启nginx -s reload时无法启动解决办法：nginx -s reload 只是用来告诉运行中的ng
UI设计中我们为什么需要设计动效 brotherlamp UI ui教程 ui视频 ui资料 ui自学
随着国际大品牌苹果和谷歌的引领，最近越来越多的国内公司开始关注动效设计了，越来越多的团队已经意识到动效在产品用户体验中的重要性了，更多的UI设计师们也开始投身动效设计领域。但是说到底，我们到底为什么需要动效设计？或者说我们到底需要什么样的动效？做动效设计也有段时间了，于是尝试用一些案例，从产品本身出发来说说我所思考的动效设计。一、加强体验舒适度嗯，就是让用户更加爽更加爽的用你的产品。
Spring中JdbcDaoSupport的DataSource注入问题 bylijinnan java spring
参考以下两篇文章： http://www.mkyong.com/spring/spring-jdbctemplate-jdbcdaosupport-examples/ http://stackoverflow.com/questions/4762229/spring-ldap-invoking-setter-methods-in-beans-configuration Sprin
数据库连接池的工作原理 chicony 数据库连接池
随着信息技术的高速发展与广泛应用，数据库技术在信息技术领域中的位置越来越重要，尤其是网络应用和电子商务的迅速发展，都需要数据库技术支持动态Web站点的运行，而传统的开发模式是：首先在主程序（如Servlet、Beans）中建立数据库连接；然后进行SQL操作，对数据库中的对象进行查询、修改和删除等操作；最后断开数据库连接。使用这种开发模式，对
java 关键字 CrazyMizzz java
关键字是事先定义的，有特别意义的标识符，有时又叫保留字。对于保留字，用户只能按照系统规定的方式使用，不能自行定义。 Java中的关键字按功能主要可以分为以下几类：（1）访问修饰符 public,private,protected p
Hive中的排序语法 daizj 排序 hive order by DISTRIBUTE BY sort by
Hive中的排序语法 2014.06.22 ORDER BY hive中的ORDER BY语句和关系数据库中的sql语法相似。他会对查询结果做全局排序，这意味着所有的数据会传送到一个Reduce任务上，这样会导致在大数量的情况下，花费大量时间。与数据库中 ORDER BY 的区别在于在hive.mapred.mode = strict模式下，必须指定 limit 否则执行会报错。
单态设计模式 dcj3sjt126com 设计模式
单例模式（Singleton）用于为一个类生成一个唯一的对象。最常用的地方是数据库连接。使用单例模式生成一个对象后，该对象可以被其它众多对象所使用。 <?phpclass Example{ // 保存类实例在此属性中 private static&
svn locked dcj3sjt126com Lock
post-commit hook failed (exit code 1) with output: svn: E155004: Working copy 'D:\xx\xxx' locked svn: E200031: sqlite: attempt to write a readonly database svn: E200031: sqlite: attempt to write a
ARM寄存器学习 e200702084 数据结构 C++c C#F#
无论是学习哪一种处理器，首先需要明确的就是这种处理器的寄存器以及工作模式。 ARM有37个寄存器，其中31个通用寄存器，6个状态寄存器。 1、不分组寄存器（R0-R7）不分组也就是说说，在所有的处理器模式下指的都时同一物理寄存器。在异常中断造成处理器模式切换时，由于不同的处理器模式使用一个名字相同的物理寄存器，就是
常用编码资料 gengzg 编码
List<UserInfo> list=GetUserS.GetUserList(11); String json=JSON.toJSONString(list); HashMap<Object,Object> hs=new HashMap<Object, Object>(); for(int i=0;i<10;i++) {
进程 vs. 线程 hongtoushizi 线程 linux 进程
我们介绍了多进程和多线程，这是实现多任务最常用的两种方式。现在，我们来讨论一下这两种方式的优缺点。首先，要实现多任务，通常我们会设计Master-Worker模式，Master负责分配任务，Worker负责执行任务，因此，多任务环境下，通常是一个Master，多个Worker。如果用多进程实现Master-Worker，主进程就是Master，其他进程就是Worker。如果用多线程实现
Linux定时Job：crontab -e 与 /etc/crontab 的区别 Josh_Persistence linux crontab
一、linux中的crotab中的指定的时间只有5个部分：* * * * * 分别表示：分钟，小时，日，月，星期，具体说来：第一段代表分钟 0—59 第二段代表小时 0—23 第三段代表日期 1—31 第四段代表月份 1—12 第五段代表星期几，0代表星期日 0—6 如： */1 * * * * 每分钟执行一次。 *
KMP算法详解 hm4123660 数据结构 C++算法字符串 KMP
字符串模式匹配我们相信大家都有遇过，然而我们也习惯用简单匹配法（即Brute-Force算法)，其基本思路就是一个个逐一对比下去，这也是我们大家熟知的方法，然而这种算法的效率并不高，但利于理解。假设主串s="ababcabcacbab",模式串为t="
枚举类型的单例模式 zhb8015 单例模式
E.编写一个包含单个元素的枚举类型[极推荐]。代码如下： public enum MaYun {himself; //定义一个枚举的元素，就代表MaYun的一个实例private String anotherField;MaYun() {//MaYun诞生要做的事情//这个方法也可以去掉。将构造时候需要做的事情放在instance赋值的时候：/** himself = MaYun() {*
Kafka+Storm+HDFS ssydxa219 storm
cd /myhome/usr/stormbin/storm nimbus &bin/storm supervisor &bin/storm ui &Kafka+Storm+HDFS整合实践kafka_2.9.2-0.8.1.1.tgzapache-storm-0.9.2-incubating.tar.gzKafka安装配置我们使用3台机器搭建Kafk
Java获取本地服务器的IP 中华好儿孙 java Web 获取服务器ip地址
System.out.println("getRequestURL:"+request.getRequestURL()); System.out.println("getLocalAddr:"+request.getLocalAddr()); System.out.println("getLocalPort:&quo

【论文翻译】Towards Robust Detection of Adversarial Examples

对抗样本的鲁棒检测

Towards Robust Detection of Adversarial Examples

摘 要

1、介绍

2、准备工作Preliminaries

2.1符号

2.2威胁模型

2.3攻击方法

3、方法Methodology

3.1非最大熵Non-maximal entropy

3.2反向交叉熵训练程序

3.3阈值测试策略

4、实验

4.1设置

4.2对正常样本的分类器

4.3 oblivious攻击下的性能

4.4白盒攻击下的性能

4.5黑盒攻击下的性能

5、结论

附录A

你可能感兴趣的:(论文翻译)

摘要