GS 算法进行一维和二维信号的相位恢复
GS 算法进行一维和二维信号的相位恢复
- 简介
- 一维信号
- 二维信号
- MATLAB代码
简介
Gerchberg-Saxton 算法可通过测量两个变换关系已知的信号的强度恢复出其相位，设原信号为 u u u, 其傅里叶变换为 U = F T [ u ] U=FT[u] U=FT[u]，测得其强度为 I = ∣ u ∣ 2 I=|u|^2 I=∣u∣2，功率谱为 P = ∣ U ∣ 2 P=|U|^2 P=∣U∣2，据此恢复出 u = ∣ u ∣ e j ϕ u=|u|e^{j\phi} u=∣u∣ejϕ的相位，步骤如下
- 初始相位设为0， u ′ = I u'=\sqrt{I} u′=I
- 计算 F T [ u ′ ] FT[u'] FT[u′]的相位 θ ′ \theta' θ′，令 U ′ = ∣ U ∣ e j θ ′ U'=|U|e^{j\theta'} U′=∣U∣ejθ′
- 计算 F T − 1 [ U ′ ] FT^{-1}[U'] FT−1[U′]的相位 ϕ ′ \phi' ϕ′，令 u ′ = ∣ u ∣ e j ϕ ′ u'=|u|e^{j\phi'} u′=∣u∣ejϕ′
- 回到步骤2，直至达到最大步数
一维信号
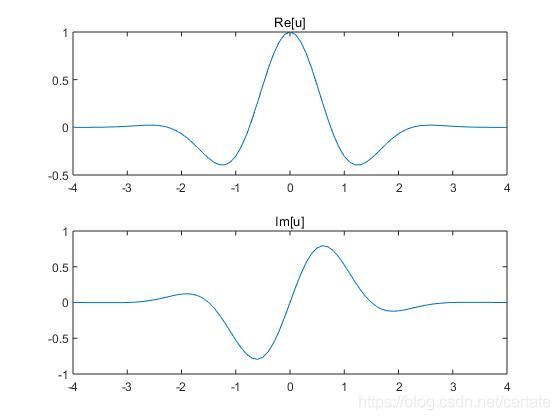
设高斯波包 u ( x ) = e − x 2 / 2 R 2 e j 2 π x / λ u(x)=e^{-x^2/2R^2}e^{j2\pi x/\lambda} u(x)=e−x2/2R2ej2πx/λ，其中 x ∈ [ − 4 , 4 ] , R = 1 , λ = 3 x\in[-4,4],R=1,\lambda=3 x∈[−4,4],R=1,λ=3，图像如下：
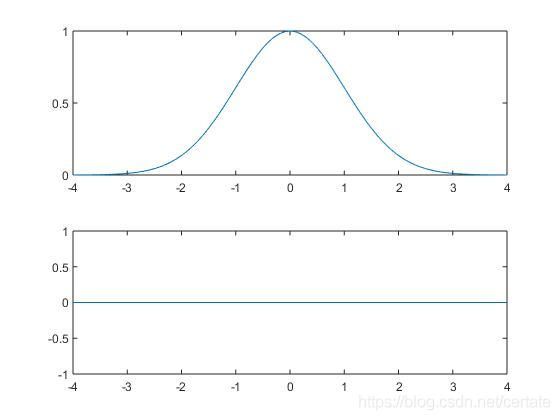
复原时，初始相位设为0，故实部为高斯函数而虚部为0：
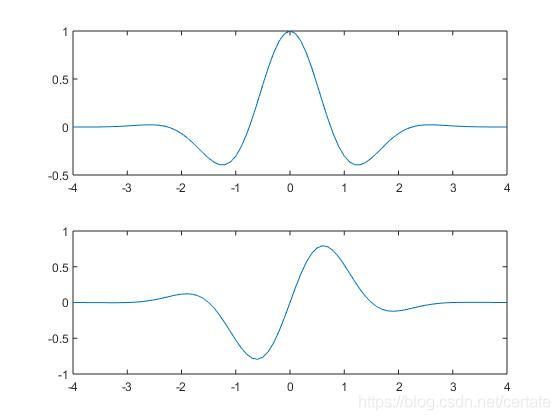
使用GS算法进行相位恢复后：
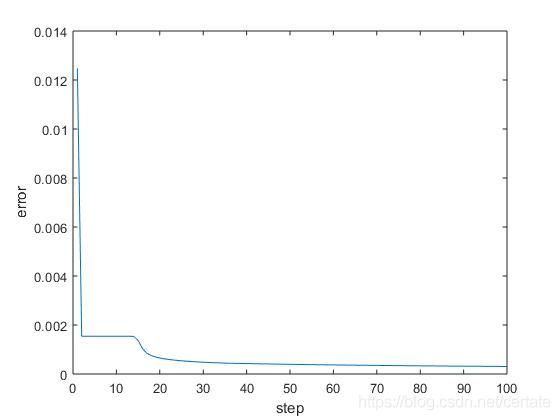
迭代过程中误差 ϵ = m e a n ( ∣ u ′ − u ∣ ) \epsilon=mean(|u'-u|) ϵ=mean(∣u′−u∣)如下:
二维信号
设 u ( x , y ) = p e a k s ( x , y ) e j 2 π r / k , r = x 2 + y 2 u(x,y)=peaks(x,y)e^{j2\pi r/k},r=\sqrt{x^2+y^2} u(x,y)=peaks(x,y)ej2πr/k,r=x2+y2，其中peaks 为MATLAB 中的函数， x , y ∈ [ − 4 , 4 ] x,y\in[-4,4] x,y∈[−4,4]， R = 1 , λ = 4 R=1,\lambda=4 R=1,λ=4, 图像如下：
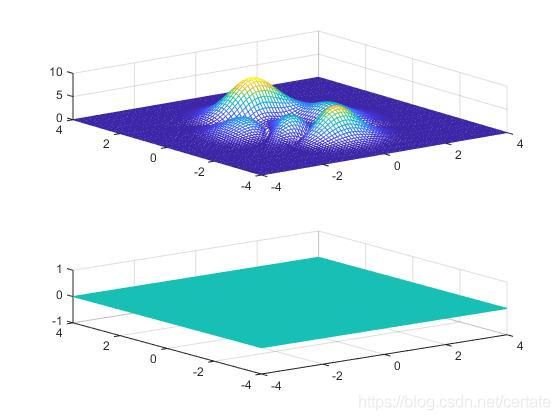
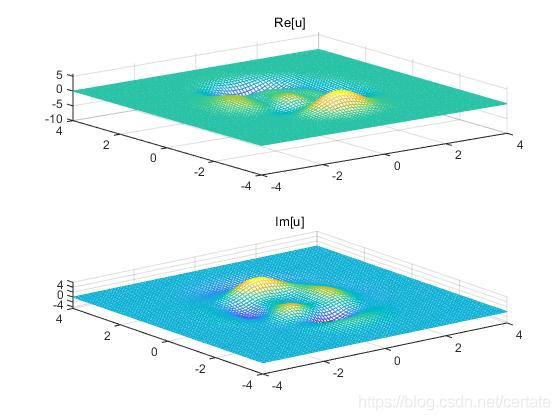初始相位设为0：
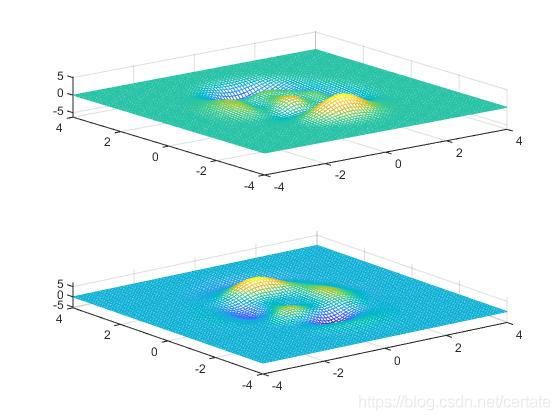
使用GS算法进行相位恢复后：
MATLAB代码
R=1;
lambda=4;
x=-4:.1:4;
N=length(x);
[X,Y]=meshgrid(x,x);
r=sqrt(X.^2+Y.^2);
r_2=sqrt((X-1).^2+(Y-2).^2);
%u=exp(-1/(2*R^2)*r.^2).*exp(1i*2*pi/lambda*r);
u=peaks(X,Y).*exp(1i*2*pi/lambda*r);
figure(1)
subplot(2,1,1)
mesh(X,Y,real(u))
title('Re[u]')
subplot(2,1,2)
mesh(X,Y,imag(u))
title('Im[u]')
u_ft=fft2(u);
figure(2)
fx=1/(N*0.1)*((1:N)-N/2);
[Fx,Fy]=meshgrid(fx,fx);
mesh(Fx,Fy,abs(fftshift(u_ft)))
u_abs=abs(u);
U_abs=abs(u_ft);
N_max=1000;
u_k=u_abs;
figure(3)
subplot(2,1,1)
mesh(X,Y,real(u_k))
subplot(2,1,2)
mesh(X,Y,imag(u_k))
error=zeros(1,N_max);
for k=1:N_max
phi_1=angle(fft2(u_k));
U_k=U_abs.*exp(1i*phi_1);
phi_2=angle(ifft2(U_k));
u_k=u_abs.*exp(1i*phi_2);
u_out=exp(-1i*angle(u_k(floor(N/2),floor(N/2))))*u_k;
error(k)=mean(mean(abs(u_out-u)));
end
figure(4)
subplot(2,1,1)
mesh(X,Y,real(u_out))
subplot(2,1,2)
mesh(X,Y,imag(u_out))
figure(5)
plot(1:N_max,error)