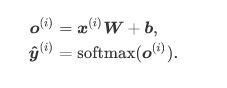动手学深度学习：task01

task01-线性模型、softmax与分类模型、多层感知机

一. 线性回归模型从零开始的实现

0.准备工作

#导入可视化的包和基本包
%matplotlib inline
import torch
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import random

print(torch.__version__)

1.生成数据集
使用线性模型来生成数据集，生成一个1000个样本的数据集，线性关系：

 price=w1⋅area+w2⋅age+b

# 输入特征
num_inputs = 2
# 样本数
num_examples = 1000

# 权重 偏差
true_w = [2, -3.4]
true_b = 4.2

features = torch.randn(num_examples, num_inputs,
                      dtype=torch.float32)
# 线性关系表达式
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()),dtype=torch.float32)

2.读取数据集

#数据迭代器
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)  # random read 10 samples
    for i in range(0, num_examples, batch_size):
        j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)]) # the last time may be not enough for a whole batch
        yield  features.index_select(0,j),labels.index_select(0, j)

3.初始化模型参数

w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32)
b = torch.zeros(1, dtype=torch.float32)

w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)

4.定义模型

def linreg(X, w, b):
    return torch.mm(X, w) + b

5.定义损失函数

#均方误差损失函数
def squared_loss(y_hat, y): 
    return (y_hat - y.view(y_hat.size())) ** 2 / 2

y_hat 是y的预测值 , y.view() 将y改变形状，
因为 y_hat 为X与w的乘积,即[n,m]与[m,1],其中n是数据的个数，m是数据特征的个数，所以 y_hat 为[n,1],而 y 为[n]
6.定义优化函数
随机梯度下降

#小批量随机梯度下降
def sgd(params, lr, batch_size): 
    for param in params:
        param.data -= lr * param.grad / batch_size # ues .data to operate param without gradient track

7.训练

# 超参数
lr = 0.03
num_epochs = 5

net = linreg
loss = squared_loss

# training
for epoch in range(num_epochs):  
    # X is the feature and y is the label of a batch sample
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y).sum()  
        # calculate the gradient of batch sample loss 
        l.backward()  
        # using small batch random gradient descent to iter model parameters
        sgd([w, b], lr, batch_size)  
        # reset parameter gradient
        w.grad.data.zero_()
        b.grad.data.zero_()
    train_l = loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))

二. softmax从零开始实现

0.准备工作

#导入基础包
import torch
import torchvision
import numpy as np
import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l

1.获取训练集数据和测试集数据

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, root='/home/kesci/input/FashionMNIST2065')

2.模型参数初始化

num_inputs = 784
num_outputs = 10
#W 、b初始化 梯度下降
W = torch.tensor(np.random.normal(0, 0.01, (num_inputs, num_outputs)), dtype=torch.float)
b = torch.zeros(num_outputs, dtype=torch.float)
W.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)

3.softmax回归模型

def net(X):
    return softmax(torch.mm(X.view((-1, num_inputs)), W) + b)

4.定义损失函数

#交叉熵损失函数
def cross_entropy(y_hat, y):
    return - torch.log(y_hat.gather(1, y.view(-1, 1)))

y.view(-1,1)是将y变形成2行1列的tensor
然后从y_hat中去取第一行中的第一个元素和第二行中的第三个元素
5.定义准确率

def accuracy(y_hat, y):
    return (y_hat.argmax(dim=1) == y).float().mean().item()

6.训练模型

num_epochs, lr = 5, 0.1

# 本函数已保存在d2lzh_pytorch包中方便以后使用
def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
              params=None, lr=None, optimizer=None):
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X, y in train_iter:
            y_hat = net(X)
            l = loss(y_hat, y).sum()
            
            # 梯度清零
            if optimizer is not None:
                optimizer.zero_grad()
            elif params is not None and params[0].grad is not None:
                for param in params:
                    param.grad.data.zero_()
            
            l.backward()
            if optimizer is None:
                d2l.sgd(params, lr, batch_size)
            else:
                optimizer.step() 
            
            
            train_l_sum += l.item()
            train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
            n += y.shape[0]
        test_acc = evaluate_accuracy(test_iter, net)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
              % (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))

train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, batch_size, [W, b], lr)

7.预测模型

X, y = iter(test_iter).next()

true_labels = d2l.get_fashion_mnist_labels(y.numpy())
pred_labels = d2l.get_fashion_mnist_labels(net(X).argmax(dim=1).numpy())
titles = [true + '\n' + pred for true, pred in zip(true_labels, pred_labels)]

d2l.show_fashion_mnist(X[0:9], titles[0:9])

三. 多层感知机从零开始实现

0.准备工作

import torch
import numpy as np
import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l
print(torch.__version__)

1.获取训练集

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size,root='/home/kesci/input/FashionMNIST2065')

2.定义模型参数

num_inputs, num_outputs, num_hiddens = 784, 10, 256

W1 = torch.tensor(np.random.normal(0, 0.01, (num_inputs, num_hiddens)), dtype=torch.float)
b1 = torch.zeros(num_hiddens, dtype=torch.float)
W2 = torch.tensor(np.random.normal(0, 0.01, (num_hiddens, num_outputs)), dtype=torch.float)
b2 = torch.zeros(num_outputs, dtype=torch.float)

params = [W1, b1, W2, b2]
for param in params:
    param.requires_grad_(requires_grad=True)
``

3.定义激活函数

```python
def relu(X):
    return torch.max(input=X, other=torch.tensor(0.0))

4.定义网络

def net(X):
    X = X.view((-1, num_inputs))
    H = relu(torch.matmul(X, W1) + b1)
    return torch.matmul(H, W2) + b2

5.定义损失函数

loss = torch.nn.CrossEntropyLoss()

6.训练

num_epochs, lr = 5, 100.0
# def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
#               params=None, lr=None, optimizer=None):
#     for epoch in range(num_epochs):
#         train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
#         for X, y in train_iter:
#             y_hat = net(X)
#             l = loss(y_hat, y).sum()
#             
#             # 梯度清零
#             if optimizer is not None:
#                 optimizer.zero_grad()
#             elif params is not None and params[0].grad is not None:
#                 for param in params:
#                     param.grad.data.zero_()
#            
#             l.backward()
#             if optimizer is None:
#                 d2l.sgd(params, lr, batch_size)
#             else:
#                 optimizer.step()  # “softmax回归的简洁实现”一节将用到
#             
#             
#             train_l_sum += l.item()
#             train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
#             n += y.shape[0]
#         test_acc = evaluate_accuracy(test_iter, net)
#         print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
#               % (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))

d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, params, lr)