基于模拟退火法的旅行商问题

基于模拟退火法的旅行商问题Matlab，请关注微信公众号“通信小课堂获取”，回复基于模拟退火法的旅行商问题

 

---

一、绪论

自从科克帕垂克、小哥拉特和瓦克奇在前人对于统计力学的研究“基础上发表了他们开创性的论文”以来，模拟退火算法被赞为解决许多高难度组合最优化问题的“救星”，并且已经被应用于诸如超大规模集成电路的计算机辅助设计、图像处理和计算机视觉、电信、经济以及其它众多工程和科学领域。

二、模拟退火算法简介

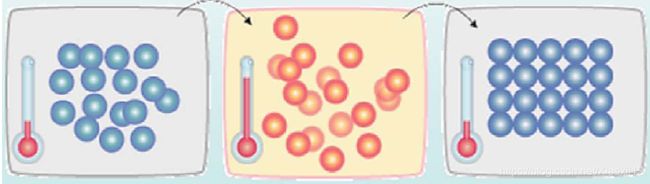
1、固体退火过程
模拟退火算法来源于固体退火原理，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随着温度升高变为无序状态，内能增大，而慢慢冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，此时内能减为最小。

 

2、模拟退火算法原理

模拟退火算法(Simulated Annealing，SA)最早的思想是由N. Metropolis等人于1953年提出。1983年,S. Kirkpatrick等成功地将退火思想引入到组合优化领域。它是基于Monte-Carlo迭代求解策略的一种随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法从某一较高初温出发，伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。模拟退火算法是一种通用的优化算法，通过赋予搜索过程一种时变且最终趋于零的概率突跳性，从而可有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法。

三、模拟退火算法目的

许多实际优化问题的目标函数都是非凸的, 存在许多局部最优解, 但是, 有效地求出一般非凸目标函数的全局最优解至今仍是一个难题。特别是随着优化问题规模的增大, 局部最优解的数目将会迅速增加.

模拟退火算法是利用问题的求解过程与熔化物体退火过程的相似性,采用随机模拟物体退火过程来完成问题的求解，也就是在控制参数(温度)的作用下对参数的值进行调整,直到所选取的参数值最终使能量函数达到全局极小值。

四、模拟退火算法流程

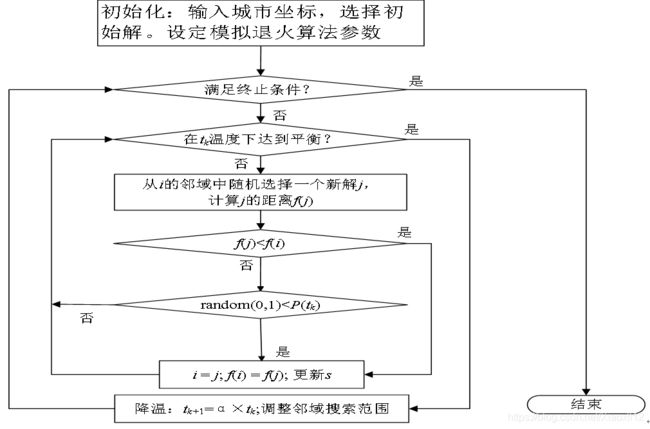
算法步骤：
Step1：针对问题选定合适的目标函数f作为能量函数E；决定初始参数:起始温度T 、终止温度、冷却率α(α∈[0,1])、单一温度迭代次数k。
Step2：设定起始迭代次数t=0，产生初始状态X0，计算其能量E0。
Step3：以目前解为中心由状态产生函数产生新的邻近解X1，计算其能量E1。
Step4：采用Metropolis接受法则比较两状态的能量，判决是否接受X1 , 若接受, 则令当前状态等于X1 , 若不接受,则令当前状态等于X0；
Step5：更新迭代次数，判断是否达到设定的阈值k，若是则进行降温T=T*α，且令t=0。
Step6：判断温度是否达到终止温度，若是则顺序执行step 7;若否则转至step 3重复执行
Step7：当前解作为最优解输出。
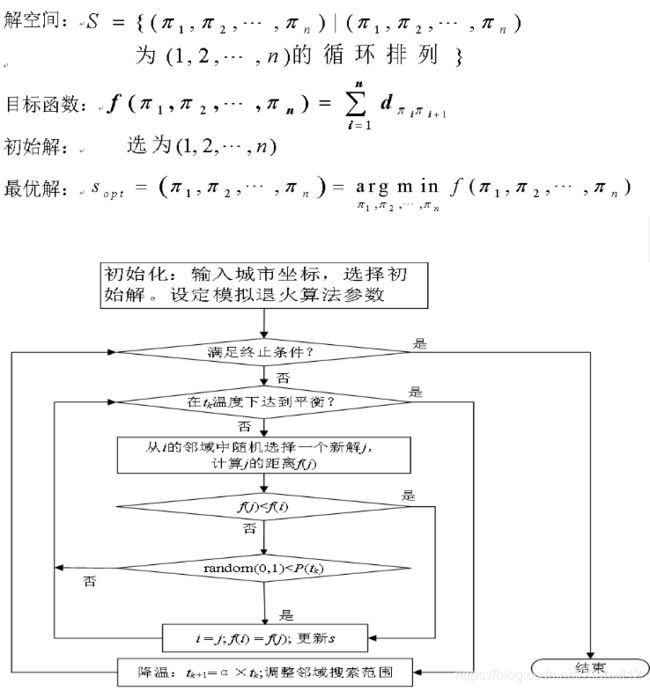
算法流程图：

五、模拟退火算法的优缺点

1、优点
（1）以一定的概率接受恶化解，引入了物理系统退火过程的自然机理，能以一定的概率接受使目标函数值变“差”的试探点,,并不强求后一状态一定优于前一状态。

（2）爬山算法与模拟退火算法比较
爬山算法：假设C点为当前解，爬山算法搜索到A点这个局部最优解就会停止搜索，因为在A点无论向那个方向小幅度移动都不能得到更优的解。
模拟退火其实也是一种贪心算法，但是它的搜索过程引入了随机因素，以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。模拟退火算法在搜索到局部最优解A后，会以一定的概率接受到E的移动。也许经过几次这样的不是局部最优的移动后会到达D点，于是就跳出了局部最大值A。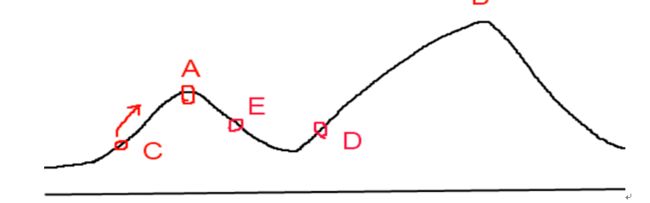
转存失败重新上传取消

（3）引进算法控制参数T
将优化过程分成各个阶段,并决定各个阶段下随机状态的取舍标准,接受函数由Metropolis算法给出一个简单的数学模型。
模拟退火算法的两个重要步骤是:一是在每个控制参数T下,由前迭代点出发,产生邻近的随机状态,由T确定的接受准则决定此新状态的取舍；二是缓慢降低控制参数T,提高接收准则,直至T->0,状态链稳定于优化问题的最优状态,提高模拟退火算法全局最优解的可靠性。

（4）使用对象函数值进行搜索
传统搜索算法不仅需要利用目标函数值,而且往往需要目标函数的导数值等其它一些辅助信息,能确定搜索方向,当这些信息不存在时,算法就失效了。而模拟退火算法仅使用由目标函数变换来的适应度函数值,就可确定进一步的搜索方向和搜索范围,无需其它的辅助信息。

（5）搜索复杂区域
模拟退火算法最善于搜索复杂地区,从中找出期望值高的区域,在求解简单问题上效率并不高。

2、缺点
（1）求解时间太长:在变量多、目标函数复杂时，为了得到一个好的近似解,控制参数T需要从一个较大的值开始,并在每一个温度值T下执行多次Metropolis算法,因此迭代运算速度慢。

（2）算法性能与初始值有关及参数敏感:温度T的初值和减小步长较难确定,如果T的初值选择较大,减小步长太小,虽然最终能得到较好的解,但算法收敛速度太慢；如果T的初值选择较小,减小步长过大, 很可能得不到全局最优解。

（3）搜索过程中由于执行概率接受环节而遗失当前遇到的最优解。

六、改进的模拟退火算法

（1）有记忆的模拟退火算法
模拟退火算法在迭代的过程中不但能够接受使目标函数向好的方向前进的解,而且能够在一定限度内接受使目标函数恶化的解,这使得算法能够有效的跳出局部极小的陷阱。然而,对于具有多个极值的工程问题,该算法就很难保证我们最终得到的最优解是整个搜索过程中曾经到达过的最优解。为了解决这个问题,我们可以给算法增加一个记忆器,使它能够记住搜索过程中曾经达到过的最好结果,这样可以在许多情况下为我们提高最终所得到的解的质量.

（2）带有单调升温的模拟退火算法
当温度T充分大的时候,相应的接受概率趋近于1,此时算法在全局进行搜索;当温度T充分小的时候,相应的接受概率趋近于O,如果搜索在此时陷入局部最优,则跳出局部最优的时间将会相当长。既然跳出局部最优的时间开销大是由于较差解的接受概率过低(也即温度过低)导致的,那么在搜索进入局部最优后,人为的升高温度,提高差解的接受概率,搜索跳出局部最优就相对会容易些,这就是单调升温过程思想的来源。

（3）并行模拟退火
设已给定了一种模拟退火模式,即已经给定了一组退火参数的取值和它们的变化规则,在区域D上按照某种分布独立地选取N个初值,同时进行计算,那么就能够得到N个结果它们可视为独立同分布的随机向量。

（4）增加补充搜索过程。即在退火过程结束后, 以搜索到的最优解为初始状态, 再次执行模拟退火过程或局部趋化性搜索。

（5）选择合适的初始状态;

（6）设计合适的算法终止准则;

七、模拟退火算法的应用

TSP（旅行商）问题是最有代表性的优化组合问题之一，其应用已逐步渗透到各个技术领域和我们的日常生活中.它一开始是为交通运输而提出的，比如飞机航线安排、送邮件、快递服务、设计校车行进路线等等。实际上其应用范围扩展到了许多其他领域，如在VLSI芯片设计、电路板布局、机器人控制、车辆选路、物流配送等方面。

旅行商问题（TSP）是旅行商要到若干个城市旅行，已知各城市之间的费用，为了节省费用，从所在城市出发，遍历所有城市后返回，问怎样才能使所走的总费用最短？

该问题属于NPC问题，主要算法有两种：
（1）穷举法：算法复杂度为O(n！)，当城市数较大时，算法运行时间无法接受，但得出的是精确解。
（2）随机搜索算法:有爬山算法、模拟退火算法、蚁群算法等。

 

 

利用MATLAB仿真结果：

 

 

 

 

八、问题

1、在利用模拟退火算法解决TSP问题的过程中，每次迭代需要产生一个新解，仿真中怎么做，依据是什么？

答：在上面的仿真中，新解的产生采用随机交换二个城市在旅行路线中的顺序的方式，交换次数随着温度的升高而较低，最低为一次。在TSP问题中新解产生方法有很多，其中常用的传统方法有三种，二点变换法、2变换法、3变换法，改进方法针对增大新解空间范围，其中我们使用的是一种改进的二点变换法。在TSP问题中对新解产生方法有一个根本的要求搜索步长足够小，即从任意初始解出发可以遍历所有解（因为任何一个解都可能是最优解），采用二点变换法可以遍历所有可能的解，且从任一解到另一解的最多的交换次数为n×(n-1)/2。除此之外在这过程中，还需要使新解空间足够大，以保证能够跳出局部最优。因为存在希望新解空间大（T较大时，即迭代初期，有利于跳出局部最优）、新解空间小（T较小时，即迭代后期）、新解产生方式可以遍历所有解，因此我们采用交换次数随温度降低而减小的二点变换法。

2、 如何从距离和迭代次数图中，判断迭代是否完成？

答：在模拟退火算法中，一般通过判断退火温度、迭代次数或者长时间未接受新解停止迭代。从距离和迭代次数的图中，若前后二次迭代的距离相差小于一定程度时，可大致判断迭代完成。当迭代次数趋向无穷大时，模拟退火算法的优化结果可以认为以概率1趋向于全局最优解，但当迭代次数有限时，得到可能只是一个较优的解，但不一定是全局最优解。