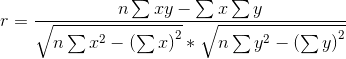python 实现相关系数计算和检验
一般情况下,总体相关系数![]() 是未知的,通常将样本相关系数r作为
是未知的,通常将样本相关系数r作为![]() 的近似估值。
的近似估值。
案例如下:
检验不良贷款与贷款余额之间的相关关系是否显著(![]() =0.05).
=0.05).
假设:![]()
import pandas as pd
import numpy as np
import scipy
import matplotlib.pyplot as plt
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文字体
plt.rcParams['axes.unicode_minus'] = False # 显示负号
columns = {'A':"分行编号", 'B':"不良贷款(亿元)", 'C':"贷款余额(亿元)", 'D':"累计应收贷款(亿元)", 'E':"贷款项目个数", 'F':"固定资产投资额(亿元)"}
data={"A":[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25],
"B":[0.9,1.1,4.8,3.2,7.8,2.7,1.6,12.5,1.0,2.6,0.3,4.0,0.8,3.5,10.2,3.0,0.2,0.4,1.0,6.8,11.6,1.6,1.2,7.2,3.2],
"C":[67.3,111.3,173.0,80.8,199.7,16.2,107.4,185.4,96.1,72.8,64.2,132.2,58.6,174.6,263.5,79.3,14.8,73.5,24.7,139.4,368.2,95.7,109.6,196.2,102.2],
"D":[6.8,19.8,7.7,7.2,16.5,2.2,10.7,27.1,1.7,9.1,2.1,11.2,6.0,12.7,15.6,8.9,0,5.9,5.0,7.2,16.8,3.8,10.3,15.8,12.0],
"E":[5,16,17,10,19,1,17,18,10,14,11,23,14,26,34,15,2,11,4,28,32,10,14,16,10],
"F":[51.9,90.9,73.7,14.5,63.2,2.2,20.2,43.8,55.9,64.3,42.7,76.7,22.8,117.1,146.7,29.9,42.1,25.3,13.4,64.3,163.9,44.5,67.9,39.7,97.1]
}
df = pd.DataFrame(data).rename(columns=columns)
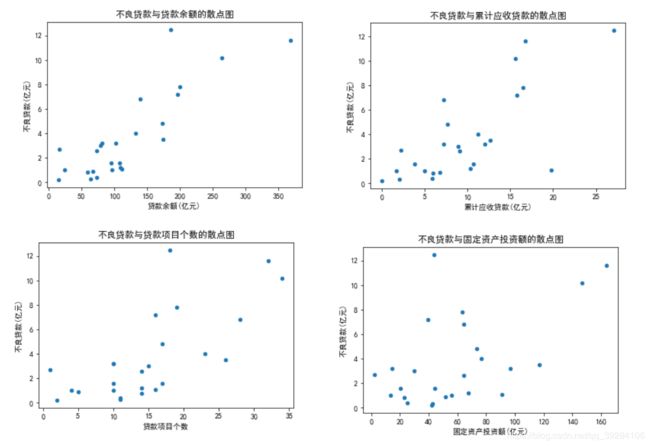
print(df)# 绘制散点图
df.plot(x='贷款余额(亿元)', y='不良贷款(亿元)', kind='scatter', title='不良贷款与贷款余额的散点图')
df.plot(x='累计应收贷款(亿元)', y='不良贷款(亿元)', kind='scatter', title='不良贷款与累计应收贷款的散点图')
df.plot(x='贷款项目个数', y='不良贷款(亿元)', kind='scatter', title='不良贷款与贷款项目个数的散点图')
df.plot(x='固定资产投资额(亿元)', y='不良贷款(亿元)', kind='scatter', title='不良贷款与固定资产投资额的散点图')相关系数公式:
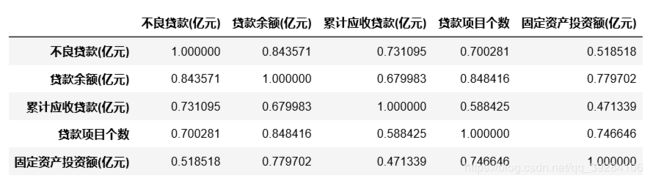
# 计算各变量之间的相关系数
corr = df.drop(columns='分行编号').corr()
print(corr)
相关系数r检验统计量公式:
# r的显著性检验
# 各个相关系数检验的统计量
def r_test_statistic(r, n):
if r==1:
return 0
else:
a = abs(r)
b = np.sqrt((n-2) / (1-r**2))
c = a*b
return c
# 计算各个相关系数检验的统计量
corr_test_stat = corr.applymap(lambda x:r_test_statistic(x, len(df)))
print(corr_test_stat)
# 根据显著性水平0.05和自由度n-2=25-2=23, 计算t分布临界值
alpha = 0.05
t_score = scipy.stats.t.isf(alpha/2, df = len(df)-2)
print(t_score)
>>> 2.068657610419041由于t=7.533515 > t_score=2.0687, 所以拒绝原假设![]() , 说明不良贷款与贷款余额之间存在显著的正线性相关关系。
, 说明不良贷款与贷款余额之间存在显著的正线性相关关系。