【题解】CF1181D Irrigation

题意

传送门

给定$M$个城市，每年会选出一个城市举办比赛，现给出前$N$年城市举办比赛的情况。在接下来的年份中，每年的比赛会在举办比赛次数最小的城市举办，如果有很多城市举办次数均为最小值，则在编号最小的城市举办比赛。现给出 $Q$个询问，每次询问第 $K$ 年在哪个城市举办比赛。

分析

由于个人习惯，把题目中的$n$和$m$意义互换。

我们可以把问题抽象成有$n$个宽度相等高度不同的矩形，给出初始高度，每次选取最矮的矩形中编号最小的，并把它的高度+1，然后不断重复这个操作，要求回答第$K$次选取的矩形的编号。

我们看到要选取编号最小的，那么毫不犹豫先排序。（遇事不决先排序）

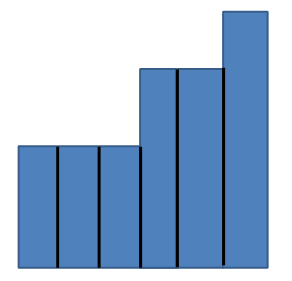
于是我们可以把原问题变成如下图一样：

我们发现有几个高度相同的矩形会组成一段“平台”。于是想想怎么求这种“平台”。

如果我单独地把一段“平台拿出来”，由于高度相同，那么它们被选择的顺序一定是按编号大小排序并形成循环的。那么假如我要在这个平台的基础上求第$k$次选择，那么我们实际上求的是这段平台中编号第$k\%len$小的（其中$len$是平台的长度，并且如果$k\%len=0$，那么就是编号最大的）。

那么这个求平台中第$k$小的操作就可以使用权值线段树平衡树维护。

---

然而很不幸，我们的问题中显然不只一个平台，所以我们考虑从低到高进行“填坑操作”。偷一张官方题解的图。

为了处理方便，我们把询问离线，按照$k$的大小（即先后顺序）排序。

比如在这张图中，前三个矩形构成了两个平台，那么我们发现高度更高的$\{2,5\}$并不会对$3$产生影响，必须得等到$3$到达$\{2,5\}$的高度后才会被影响。那么我们就可以放心地先把$3$填至$\{2,5\}$的高度，然后把$3$加入到平台中形成$\{2,3,5\}$这样的一个平台。显然经过填坑操作后，所有的平台都是原序列的前缀。在填坑过程中，有一些询问是可以被回答的，那么就通过平台的性质进行回答。同时我们也要把新加入到平台的元素插入到权值线段树中，以便下一次查询。

---

实现细节

在处理平台和询问的时候可以分别记录一个指针，表示当前处理到哪一个矩形或询问。同时再维护一个$now$表示当前已经进行了几次选择（初始值为给定的已操作次数）。然后对于矩形，每次向后找到一个平台，在此过程中把平台中的矩形编号插入到权值线段树中。接着向后枚举询问，如果当前的$now$加上下一个平台被填满所需的操作次数大于询问，那么说明这个询问可以在这次填坑中被回答，那么在权值线段树中查询得到答案。最后$now$累加上填坑所需操作次数即可。

复杂度

我们的两个指针都是线性扫描的，所以处理询问部分是$O((n+q)logn)$的，由于前面需要一遍排序也需要$O(nlogn)$的时间，所以总复杂度$O((n+q)logn)$。

代码

#include 
#define ll long long
#define MAX 500005
#define lc(x) (x<<1)
#define rc(x) (x<<1|1)
#define mid ((l+r)>>1)
using namespace std;

namespace sgt{
    int s[MAX*4];

    void push_up(int p){
        s[p] = s[lc(p)]+s[rc(p)];
    }

    void update(int p, int l, int r, int u, int k){
        if(l == r){
            s[p] += k;
            return;
        }
        if(mid >= u) update(lc(p), l, mid, u, k);
        else update(rc(p), mid+1, r, u, k);
        push_up(p);
    }

    int query(int p, int l, int r, int k){
        if(l == r) return l;
        if(s[lc(p)] >= k){
            return query(lc(p), l, mid, k);
        }
        else return query(rc(p), mid+1, r, k-s[lc(p)]);
    }
}
//以上权值线段树模板

struct ask{		//询问离线
    ll k, id;
    friend bool operator <(ask a, ask b){
        return a.k < b.k;
    }
}q[MAX];

struct city{		//矩形
    ll h, id;

    friend bool operator <(city a, city b){
        if(a.h == b.h) return a.id < b.id;
        return a.h < b.h;
    }
}a[MAX];

int n, m;
ll Q, now, p, p1, p2, ans[MAX];

int main()
{
    cin >> m >> n >> Q;
    for(int i = 1; i <= n; ++i){
        a[i].id = i;
    }
    ll x;
    for(int i = 1; i <= m; ++i){
        scanf("%lld", &x);
        a[x].h++;
    }
    sort(a+1, a+n+1);
    for(int i = 1; i <= Q; ++i){
        scanf("%lld", &q[i].k);
        q[i].id = i;
    }
    sort(q+1, q+Q+1);
    //初始化：排序、离线

    p1 = p2 = 1;
    now = m;
    while(p1 <= n){
        p = p1;
        while(a[p].h == a[p1].h){		//向后找平台，并插入到权值线段树中
            sgt::update(1, 1, n, a[p].id, 1);
            p++;
        }
        while(now+(a[p].h-a[p1].h)*(p-1) >= q[p2].k){		//处理在这次填坑范围内的询问
            ll t = (q[p2].k-now)%(p-1);
            if(!t) t = p-1;
            ans[q[p2].id] = sgt::query(1, 1, n, t);
            p2++;
        }
        now += (a[p].h-a[p1].h)*(p-1);		//累加操作次数
        p1 = p;			//下一次平台的开始
    }
    for(int i = 1; i <= Q; ++i){
        //可能还有一些询问没有处理，但此时所有矩形都已形成一个平台，直接回答，甚至不需要权值线段树
        if(!ans[q[i].id]){
            ll t = (q[i].k-now)%n;
            if(!t) t = n;
            ans[q[i].id] = t;
        }
    }
    for(int i = 1; i <= Q; ++i){
        printf("%lld\n", ans[i]);
    }

    return 0;
}