2.2 贪心算法

 贪心算法

    贪心算法就是遵循某种规则，不断贪心的选取当前最优策略的算法设计方法。

 

题一、硬币问题

    有1元、5元、10元、50元、100元、500元的硬币各C1，C5，C10，C50，C100，C500枚。现在要用这些硬币来支付A元，最少需要多少枚硬币？假设本题至少存在一种支付方案。 
    限制条件： 
           0<=C1，C5，C10，C50，C100，C500<=10^9
           0<= A <= 10^9

          输入：C1 = 3   C2 = 2     C10 = 1    C50 = 3    C100 = 0      C500 = 2    A = 620 

          输出： 6（500元硬币1枚，50元硬币2枚，10元硬币1枚，5元硬币2枚，合计6枚） 

         解题思路：为了尽量地减少硬币的数量，我们首先得尽可能多地使用500元硬币，剩余部分尽可能多地使用100元硬币，剩余部分尽可能多地使用50元硬币，剩余部分尽可能多地使用10元硬币，再剩余部分尽可能多地使用5元硬币，最后的部分使用1元硬币支付。

#include 
#include 

//void min(int i,int j)
//{
//	if(i>j)
//		return j;
//	if(j>i)
//		return i;
//}

void solve(int A){	
	const int V[6] = {1,5,10,50,100,500};
	const int C[6] = {100,100,100,100,100,100};
	int ans=0;//硬币枚数 
	
	for(int i=5;i>=0;i--)
	{
		//int t=min(A/V[i],C[i]);
		int t = A/V[i];
		A -= t*V[i];
		ans += t;
	}
	
	printf("%d\n",ans);
}

int main(){
	int A;
	scanf("%d",&A);
	void solve(int A);
	
	solve(A);
}

 

 

题二、区间问题

问题描述：

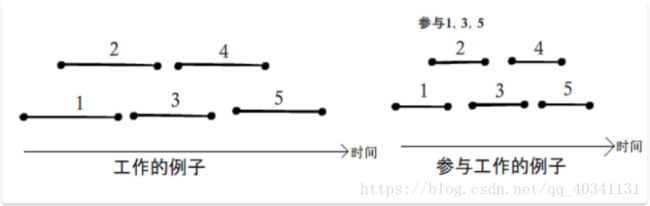
    有n项工作，每项工作分别在si开始，ti结束。对每项工作，你都可以选择参加或不参加，但选择了参加某项工作就必须至始至终参加全程参与，即参与工作的时间段不能有重叠(即使开始的时间和结束的时间重叠都不行)。

限制条件：

    1<=n<=100000

    1<=si<=ti,=10^9

样例：

    输入

        n = 5, s= {1,2,4,6,8}, t={3,5,7,9,10}

    输出

       3(选择工作1, 3, 5)

解题分析：

    对这个问题，如果使用贪心算法的话，可能有以下几种考虑：

    (1)、每次选取开始时间最早的；

    (2)、每次选取结束时间最早的；

    (3)、每次选取用时最短的；

    (4)、在可选工作中，每次选取与最小可选工作有重叠的部分；

只有（2）是正确没有反例的；

#include 
#include 

const int MAX_N = 100000;
int N = 5,S[MAX_N] = { 1,2,4,6,8 }, T[MAX_N] = { 3,5,7,9,10 };
//N项工作，S为开始时间，T为结束时间

//pair itv[MAX_N];//用于对工作排序的pair数组
 pair 默认对first升序，当first相同时对second升序；
//

 
void sort(int S[],int T[])
{
	 int j=0;
	 int sw0,sw1;
 
	 while(j<5)
	 {
		  for(int i=0;i<4;i++)
		 {		 	
		 	if(T[i] > T[i+1])
		 	{	
		 		sw0 = T[i];
		 		sw1 = S[i];
		 		
		 		T[i] = T[i+1];
		 		S[i] = S[i+1];
		 		
		 		T[i+1] = sw0;
		 		S[i+1] = sw1;
			 }
			 
			 if(T[i] == T[i+1])
			 {
			 	if(S[i] < S[i+1])
			 	{
			 		sw0 = T[i];
		 			sw1 = S[i];
		 		
		 			T[i] = T[i+1];
		 			S[i] = S[i+1];
		 		
		 			T[i+1] = sw0;
		 			S[i+1] = sw1;
				 }
			 }
		 }
		 j++; 
	}
	int ans = 0, t = 0;//t是最后所选工作结束的时间
    /*
    结束时间小于下一个最先结束可执行时间，
    */
    for (int i = 0; i < N; i++) 
    {
        if (t < S[i])//判断区间是否重叠  
        {
            ans++;
            t = T[i];
        }
    }
    //cout << ans << endl;
    printf("%d",ans);
	
	
	
 } 

void solve()
{
//    for (int i = 0; i < N; i++)
//    {
//        itv[i].first = T[i];//开始时间 
//        itv[i].second = S[i];//结束时间 
//    }
    /*
    sort:首先根据first进行排序，first数据相同根据second排序【重点（注意sort执行的过程）】
    按照由小及大进行排序，即按照结束时间最小进行排序，结束时间相同按照开始时间最小进行排序。
    */
    sort(S, T);
//    int ans = 0, t = 0;//t是最后所选工作结束的时间
//    /*
//    结束时间小于下一个最先结束可执行时间，
//    */
//    for (int i = 0; i < N; i++) 
//    {
//        if (t < T[i])//判断区间是否重叠  
//        {
//            ans++;
//            t = S[i];
//        }
//    }
//    //cout << ans << endl;
//    printf("%d",ans);
}
int main() {
    solve();
    
    return 0;
}

 

 

题三、Best Cow Line（POJ 3617)

问题描述：

    给定长度为N的字符串S，要构造一个长度为N的字符串T。期初，T是一个空串，随后反复进行下列任意操作：

    1>从S的头部删除一个字符，加到T的尾部； 
    2>从S的尾部删除一个字符，加到T的尾部。

目标是要构造字典序尽可能小的字符串T。

举例：

    比如当N=6，S=”ACDBCB”时，程序应输出ABCBCD。

思路： 
将S反转后的字符串定为S’，比较S和S’的字典序，如果S较小则从S开头取字符加到T的末尾，反之从S末尾取字符加到T的末尾。字典序相同时两者等价，取哪个都行。

字典排序（lexicographical order）是一种对于随机变量形成序列的排序方法。其方法是，按照字母顺序，或者数字小大顺序，由小到大的形成序列。

#include 
#include 

char T[10],S[10],K[10];

int main()
{
	int n,k=0,a=0,b=0;
	while(scanf(" %d",&n) != EOF)
	{
		int L=n;
		for(int i=0;i=0;j--)
		{
			S[j]=T[k];
			k++;
		}
	
		//T[m]是正，S[a]是反 
		for(int m=0;m<=n;m++)
		{
			
			if(T[m]>S[a])
			{
				K[b]=S[a];
				a++;
				b++; 
				m--;
				n--;
			}
			
			if(T[m]==S[a])
			{
				K[b]=S[a];
				a++;
				b++;
				m--;
				n--;
			}
			
			if(T[m]

 

题四、Saruman's Army（POJ 3069）

问题描述：

    直线上有n个点，点i的位置是Xi。从这n个点中选择若干个，给它们加上标记。对每一个点，其距离为R以内的区域里必须有带标记的点（本身为带有标记的点，可以认为与其距离为0的地方有一个带有标记的点）。在满足这个条件的情况下，希望能为尽可能少的点添加标记。求最少要有多少个点被加上标记。

限制条件：

• 1<= N <=1000
• 0<= R <=1000
• 0<= Xi <=1000

/*
6
10
1,7,15,20,30,50
*/
#include 
#include 


void solve(int a[],int N,int R)
{
	int i=0;
	int ans=0;
	
	while (i < N)
	{
		int start1 = a[i++];//标记一个点 
		//一直向右前进直到距离标记点距离大于R 
		while(i < N && start1 + R >= a[i])
		{
			i++;
		}
		
			
		int start2 = a[i-1];//标记点 
		//一直向右前进直到距离标记点距离大于R 
		while (i < N && start2 + R >= a[i])
		{
			i++;
		}
		ans++;
	}
	printf("%d",ans);
}

void sort()
{
}


int main()
{
	int N,R;
	int a[100];
	scanf("%d",&N);
	scanf("%d",&R);

	if(N>=1 && R>=0)
	{
		for(int i=0;i

 

题五、Fence Repair( POJ 3253)

问题描述：

     农夫约翰为了修理栅栏，要将一块很长的木板切割成N块。准备切成的木板长度为L1、L2、···、LN，未切割之前木板的长度恰好为切割后木板长度的总和。每次切割木板时，需要的开销为这块木板的长度。例如长度为21 的木板要切成长度为5、8、8的三块木板。长21的木板切成长为13和8的板时，开销为21.再将长度为13的板切成长度为5和8 的板时，开销是13.于是合计开销为34。请求出按照目标要求将木板切割完最小的开销是多少。（1<=N<=20000,0<=Li<=50000） 
输入样例： 
    N=3，L=（8,5,8） 
输出 
    34

解题思路：

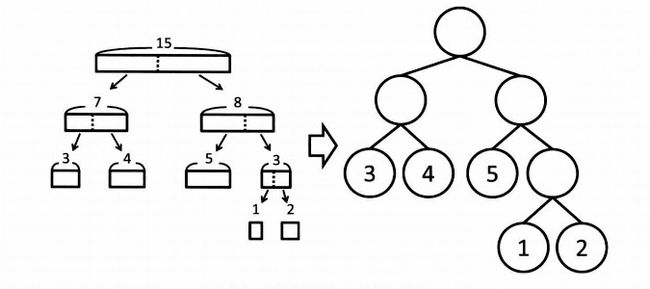
    我们首先试图分割一块长为15的木板：

    

    这里的每一个叶子节点对应了切割出的一块块木板，叶子节点的深度就对应了为了得到对应木板所需的切割次数，开销的合计就是各叶子节点的

    木板的长度 X 节点的深度

    于是可知，此时的最佳切割方法首先应该具有如下性质：

         最短的板与次短的板的节点应当是兄弟节点

    对于最优解来讲，最短的板应当是深度最大的叶子节点之一。所以与这个叶子节点同一深度的兄弟节点一定存在，并且由于同样是最深的叶子节点，所以应该对应于次短的板。

/*
3
8 5 8 
*/ 
#include
using namespace std;
const int max_n=20000;
int l[max_n+1];
int n;
int ans=0;
int main()
{
    cin>>n;
    for(int i=0;i>l[i];
    }

    //计算到木板为1块为止
    while(n>1)
    {
        //求出最短的板mii1和次短的板mii2
        int mii1=0,mii2=1;
        if(l[mii1]>l[mii2]) swap(mii1,mii2);
        for(int i=2;i