FPGA之道(59)时空变换之时域优化
文章目录
- 前言
- 时空变换之基本概念
- 时空概念简介
- 时空变换方案
- 时空变换之时域优化
- 逻辑化简
- 逻辑化简讨论
- 空域方面的颠倒现象
- 时域方面的颠倒现象
- 逻辑化简总结
- 结构调整
- 分布调整
- 思路转换
- 提前进位法提高多级累加器的工作频率
- 布局调整
前言
疫情已经持续到了3月,今天是三月初,前几日在修改论文,想来今天是新的一月的开始,应该更新博客了,日子虽然都是数字,但有些日子注定拥有特殊的记号。
本来想着应该更新数的表示以及数的运算,但是确实在FPGA中完成原本我们认为十分简单的东西具有一定的难度,十分的繁琐,还是更新下FPGA设计的思路,今天是有关时空转换的,为了博文不能太长,选择分为几部分来更新。
本文依然选自《FPGA之道》,让我们站在巨的肩膀上,开始冲鸭。
时空变换之基本概念
时空概念简介
时钟速度决定完成任务需要的时间,规模的大小决定完成任务所需要的空间(资源),因此速度与规模其实就是FPGA设计中时间与空间的体现。对于FPGA设计来说,时间和空间这两因素就好比阴、阳之于太极,乾、坤之于八卦一样,它们相互依存却又相互制约,唯有达到平衡,方可天下太平。
如果要提高FPGA设计的时钟速率,那么每一个时钟周期内组合逻辑所能做的事情通常就越简单,因此为了实现同样的功能往往会造成资源的膨胀。与此同时,由于时钟速度越快,对资源排列关系的要求就越紧凑,可是资源的膨胀会导致资源占用率提高,进而导致在FPGA芯片内进行布局布线的难度增大,这也就导致资源更难变得紧凑,从而又会给时钟速度的提高带来一定的负面影响。
如果要降低FPGA设计的规模,一般来说,以前多个模块做的事情就需要由一个模块来完成,那么为了能在同样的时间内完成同样的任务,那么就必须提高该模块的执行速度,即时钟频率,而时钟频率的提高又可能会导致该模块一定的资源膨胀,从而又会给设计规模的降低带来一定的负面影响。
上面的讨论中蕴含了FPGA设计的时空互换定律,那就是——如果时间吃紧,空间有余,就拿空间来换时间,虽然空间的增加可能对时间又会产生一些负面影响,但是通常利大于弊;反之,如果空间吃紧,时间有余,就拿时间来换空间,虽然时间的减少可能对空间又会产生一定负面影响,但是通常利也是大于弊的。
鉴于此,可以推断出:如果FPGA设计的规模预期比较大,那么它布局布线的难度就会较大,同一功能聚类的资源就较难紧密排列,因此时钟速度就不可能太高,如果FPGA设计的时间预期也比较高,那么由于时钟速度的限制,要在规定的时间内完成同样的任务就需要更多的资源来实现任务分担,这又反过来导致了设计规模的变大。因此现实中,不可能存在时间、空间均最优的FPGA设计,若要这么做,无异于痴人说梦。但是残酷的现实往往会逼迫每一名FPGA开发者朝这个方向进行努力,因为随着集成度的越来越高、功能需求的越来越复杂等等因素,客观环境要求我们必须设计出又快又省的FPGA设计才能够最终完成项目、迅速赢得市场。因此,为了满足各种苛刻的需求,每一个FPGA开发者都必须了解并能运用时空变换的相关技术,以使自己的设计达到时间、空间的综合最优。
那么由时空互换定律出发,凡是能够在这两种因素之间做到随意调配的人,必是FPGA设计师中的“大虾”!凡是能够根据实际情况达到时空完美平衡点的作品,必是FPGA设计中的“杰作”!因此,写HDL代码前先对自己的FPGA设计做一个时空的评估,找准设计的时空平衡点,是指导整个设计走向的重要参考。
时空变换方案
当FPGA设计的性能或者预期的性能不能满足项目的需求时,就是需要运用时空变换定理的时候。总的来说,时空变换定理在运用时可以具体划分为四项工作内容,即——时域优化、空域优化、时间换空间以及空间换时间。 那么当我们需要对FPGA设计的性能进行优化时,通常的做法应该是这样的:
- 首先,利用时域优化来去除设计在时间方面的冗余,利用空域优化来去除设计在空间方面的冗余。如果这样处理后的设计已经能满足需求,那最好不过;即使仍然达不到要求,经过如此处理后的设计也分别在空间和时间上腾出了更多的余量,而余量是时空变换定理得以应用的前提。
- 其次,根据设计与需求之间的矛盾,如果是时间不够了,那么就想办法用空间换时间;如果是空间不够了,那么就想办法用时间换空间。
- 第三,由于一些时空变换的方法会改变原有逻辑电路的组织结构,因此变换后的逻辑电路很可能具有进一步进行时域优化、空域优化的余地,所以可以利用这一点进一步提升逻辑电路的性能。
- 最后,在FPGA设计中,没有什么方案是永远最优的,也没有什么方案是永远最差的,我们所要做的并不是竭尽全力去找寻最优的方案,而应该是集中精力找到最适合当前需求的方案。
上述即为常用的时空变换方案,接下来将具体讨论时空变换时所涉及到的四类工作:
时空变换之时域优化
本小节我们主要关注时域内部的优化方法。注意,在做时域优化时,往往是不以牺牲空域余量为前提的,因为它的目的主要是去除时域内部的一些冗余。接下来,将为大家介绍几类比较常用的时域优化方法:
逻辑化简
逻辑化简讨论
逻辑化简是最最基本的冗余去除方法,也是最最有效的冗余去除利器。无论是针对组合逻辑还是时序逻辑,异或是针对时域还是空域,逻辑化简会给所有方面都带来好处。因为逻辑简化了,首先实现该功能需要的逻辑门和触发器数量往往就会减少,因此组合逻辑和时序逻辑中的冗余都得以剔除,进而对空域带来了优化效果;其次,组合逻辑更加精简了,布局布线更加容易了,时域更容易达到较好的性能,并且逻辑的化简很可能导致组合逻辑的级数减少,而这将直接对时域的性能产生大幅提升。
当然,编译器在对FPGA设计进行编译的过程中,也会同时对逻辑进行一些优化,不过其程度毕竟有限。并且,作为一个合格的FPGA开发者来说,应该更多的掌握自己的命运,而不是交由编译器去处置。因此在进行FPGA设计及HDL代码描述时,我们还是应该注重多做一些逻辑化简工作的,不求将所有逻辑都化简到最简,但求不要在我们的FPGA设计中存在过多较为明显的冗余。
逻辑化简的方法有很多种,这里就不再赘述。不过由于FPGA内部硬件组织结构的特殊性,导致有时候略微复杂一些的逻辑实现起来并不一定比简单的逻辑占用资源多,甚至有时候资源更省,空域性能更好;也会导致有时候略微复杂一些的逻辑实现起来并不一定比简单的逻辑时间延迟大,甚至有时候延迟更小,时域性能更好。当然了,这种由于FPGA硬件结构导致的逻辑时空性能颠倒仅仅是细节方面的微观可能,大部分时候其变化趋势仍然是与逻辑化简的程度保持一致的,而从宏观上来看,仍然是越简单的逻辑,其时空性能越好。
其实,在FPGA中,会导致时空性能出现反常现象的主要原因就是其内部的查找表(LUT)资源。通过【知己知彼篇->FPGA内部资源介绍->逻辑资源块】小节的介绍,我们了解到,FPGA内部实现组合逻辑的主要载体就是LUT资源。通常来说,为了使每个LUT都能够实现功能适中的组合逻辑,FPGA内部的LUT一般都是3、4、5或6输入的,但输出都仅有1个。因此,编译器总是要面临着将我们所描述的组合逻辑映射为多输入、单输出的LUT集合形式的工作,而这一工作,就有可能导致微观上的时空性能颠倒。不过随着编译器版本的不断更新,编译技术的不断进步,这种微观上的时空性能颠倒的可能性也会越来越小,但是作为一个FPGA开发者来说,还是有必要了解一下这种情况的具体表现和成因的,下面就来具体介绍:
空域方面的颠倒现象
有时候,逻辑上的化简并不会为最终的FPGA资源占用带来好处,例如对于以下逻辑:
![]()
这是一个3输入、1输出的组合逻辑,存在着明显的冗余,可以化简为:
F = AB + AC +BC;
化简后的组合逻辑显然会消耗更少的逻辑门,但仍为3输入、1输出的组合逻辑。那么对于一个内部仅有4输入、1输出LUT的FPGA芯片来说,这一逻辑化简过程是毫无任何意义的,因为无论是原来存在冗余的3输入组合逻辑还是化简后的3输入组合逻辑,它们的输出都仅有1个,因此编译器最终都是使用一个4输入、1输出的LUT来实现上述逻辑函数功能的,因此化简前后对于FPGA内部资源的占用没有任何影响。
有时候,逻辑上的化简甚至还会为最终的FPGA资源占用带来更多的负担,例如对于以下逻辑:
F = AB + CD + MN;
这是一个精简的6输入、1输出组合逻辑,并不存在冗余,但是如果FPGA芯片内部仍然仅有4输入、1输出的LUT,那么将该组合逻辑映射为LUT的结果大概如下图所示:
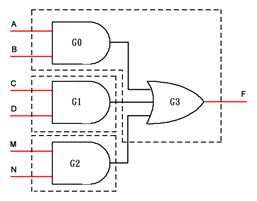
上图中,每一个虚线框内的组合逻辑部分都被映射为FPGA芯片内部的1个LUT资源,因此上述组合逻辑共占用3个4输入、1输出的LUT资源。注意,左下部分的两个小虚线框显然没有充分利用LUT的4输入特性,但是由于它们各有输出,因此也无法合并。
倘若略微复杂一下上述组合逻辑,将其变化为:
F = (AB + CD) + MN;(注意,两个两输入或门比一个三输入或门要耗资源)
那么新的映射结果将如下图所示:

从上图可以看出,这一个略微复杂一点的功能等价组合逻辑,共占用2个4输入、1输出的LUT资源,比之前节省的1个LUT资源。
继续在上述逻辑中添加冗余,将其变化为:
F = (AB + CD) + (MN + (AB + CD));
重新进行映射工作,可得新的结果如下:

由此可见,即便是一个存在如此明显冗余的组合逻辑,最终也仅占用了FPGA芯片中的2个LUT资源。
时域方面的颠倒现象
有时候,逻辑上的化简并不会为最终的FPGA时序指标带来好处,例如对于以下逻辑:
F = (AB + BC)AC;
这是一个3输入、1输出的组合逻辑,存在着明显的冗余,可以化简为:
F = ABC;
化简后的组合逻辑显然具有更少的逻辑门级(原来3级门延迟,现在仅1级门延迟),但仍为3输入、1输出的组合逻辑。那么对于一个内部仅有4输入、1输出LUT的FPGA芯片来说,这一逻辑化简过程是毫无任何意义的,因为无论是原来存在冗余的3输入组合逻辑还是化简后的3输入组合逻辑,它们的输出都仅有1个,因此编译器最终都是使用一个4输入、1输出的LUT来实现上述逻辑函数功能的,因此化简前后LUT的级数都为1,所以化简工作对于FPGA的时序指标是没有任何影响的。
有时候,逻辑上的化简甚至还会为最终的FPGA时间性能带来额外的负担,例如对于以下逻辑:
![]()
上述是一个明显具有冗余的组合逻辑,如果FPGA芯片内部的一个逻辑资源块具有六个4输入、1输出LUT和三个3输入、1输出的LUT,那么上述具有冗余的组合逻辑需要使用五个4输入、1输出的LUT来实现,正好可以放置于一个逻辑资源块内。但若将上述组合逻辑化简为如下形式:
F = ABC + ABD + ACD;
那么此时需要四个3输入、1输出的LUT来实现,由于一个逻辑资源块内最多只有三个这种规格的LUT,因此,为了实现上述化简后的逻辑必须跨越至少两个逻辑资源块。但是,这样做的代价是要增加走线的长度,所以化简后的逻辑在被映射为LUT的形式后,时域方面的性能反而更差了。
逻辑化简总结
综上所述,恰恰也正是由于这种FPGA编译时从逻辑门到LUT的映射过程,会导致太为细节的逻辑化简对时空性能没有影响甚至出现反常的现象,因此再加上编译器本身的优化功能,便为广大FPGA开发者们带来了巨大的福音!那就是我们无需严格按照【共同语言篇->数字逻辑电路基础知识->数字逻辑的化简】章节中介绍的那些化简方法,也无需绞尽脑汁、废寝忘食的去关注每一部分组合逻辑并力求达到最简,而仅需在我们的HDL代码中稍作注意,剔除明显且过分的组合逻辑冗余即可。
结构调整
结构调整是提高时域性能的另一种方法,它是在不改变原有组合逻辑功能的前提下,通过调整其内部逻辑门之间的连接关系,来达到减少逻辑门级数的目的,进而提高时域性能的方法。举例如下:
现在有同步输入总线A、B、C、D,需要在下一时钟周期就能以寄存的方式输出它们的和SUM。那么通常来说,你可能会将HDL代码写成这样:
-- VHDL example
-- all inputs are bus type
process(clk)
begin
if clk'event and clk = '1' then
SUM <= A + B + C + D;
end if;
end process;
// Verilog example
// all inputs are bus type
always@(posedge clk)
begin
SUM <= A + B + C + D;
end
对于上述代码,编译器通常会将它翻译成如下电路:

由此可见,该电路中从“输入A~D”到“输出SUM的寄存器输入”之间,最长的逻辑路径依次经过了3个加法器,也就是说上述电路中的组合逻辑部分有3级加法器,如果一个加法器的时间延迟为T的话,那么整个组合逻辑的时间延迟就是3T。
编译器之所以会给出如此结构的电路,主要是因为在HDL语言中,“+”运算符号对应的运算优先关系为从左至右,因此A、B先参与运算,而其结果再和C一起送入下一个加法器运算,而这次的结果再和D一起送入第三个加法器进行运算,至此才得到组合形式输出的和。通过进一步分析上述电路,我们可以发现,当A、B进行运算时,C、D其实闲着没事干(虽然事实不是这样,但是此时第二、第三个加法器进行的运算都是无效的),因为第一、第二个加法器的输出还没有稳定;而当A、B或C参与有效运算时,D其实一直是闲着没事干的(解释类似同前),因为第二个加法器的输出还没有稳定。由此可见,上述电路中的逻辑结构不是很合理,因为我们更希望编译器得出的电路是同时使用两个加法器分别处理A、B和C、D的求和,然后再使用一个加法器处理这两个加法器的结果即可。为了达到这种效果,我们可以对上例进行一些修改,结果如下:
-- VHDL example
-- all inputs are bus type
process(clk)
begin
if clk'event and clk = '1' then
SUM <= (A + B) + (C + D);
end if;
end process;
// Verilog example
// all inputs are bus type
always@(posedge clk)
begin
SUM <= (A + B) + (C + D);
end
可见,我们仅仅通过添加了两个小括号,就调整了原有算式中不太合理的运算优先级关系,这便是“小括号的妙用”。对应上述代码,编译器给出的电路结构如下:

由此可见,该电路中从“输入A~D”到“输出SUM的寄存器输入”之间,最长的逻辑路径依次经过了2个加法器,也就是说上述电路中的组合逻辑部分仅有2级加法器(虽然从资源的角度上来说它仍然包含3个加法器),那么此时,整个组合逻辑的时间延迟减小到了2T,这极大的提高了上述求和电路在时域方面的性能。
关于上例,有一点需要注意,那就是参与运算的A ~ D全部都是总线,也就是说它们的数据位宽应该都大于1bit。如果数据位宽仅为1bit的话,编译结果会略有不同,因为每个加法器还具有一位进位输入位,这样对于1bit的输入来说,可以完成三个输入的求和,那么此时的小括号就要以3个输入为一组来进行时域优化了。例如,若对于A~J这9个1bit位宽的输入信号求和,时域优化后的写法应该如下:
-- VHDL example
-- all inputs are 1 bit
process(clk)
begin
if clk'event and clk = '1' then
SUM <= (A + B + D) + (E + F + G) + (H + I + J);
end if;
end process;
// Verilog example
// all inputs are 1 bit
always@(posedge clk)
begin
SUM <= (A + B + D) + (E + F + G) + (H + I + J);
end
编译器给出的对应结果电路如下:

当然了,真要是输入全为1bit的话,加法也就完全变成了异或操作,我们也就没有必要使用全加器来实现求和功能。
对比上述两个运用了时域优化后的例子,可以发现结构调整的思路跟组合逻辑内部基本逻辑单元的输入端口数量相关,而结构调整的最终目的是希望把各个输入视为叶子节点,把输出视为根节点,最终组建出深度最小的树。(树的概念可以参考《数据结构》相关书籍)
分布调整
分布调整又叫时间调整,英文用retiming来表示。它是基于这样一个事实而产生的,即一个设计的时间性能取决于其中延迟最大的那部分组合逻辑,这类似短板效应,原理详见下图:

上图中,由于组合逻辑1的复杂度远高于组合逻辑2,因此整个时序电路的时间性能完全受制于组合逻辑1的时间延迟指标,而与组合逻辑2这部分无关。因此,在不牺牲空间余量的前提下,在不改变原有逻辑功能的前提下,为了能够让“短板变长”,可以采用从其它“长板子”上截取一节并拼接到“短板”上的方法,来达到时域性能的提升,原理详见下图:
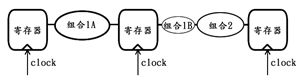
由此可见,该方法的具体操作就是,从时序电路中最复杂的组合逻辑1中拿走一小部分逻辑(组合逻辑1B),并将其移至之前逻辑复杂度较小的组合逻辑2所处的位置,这样将使得原组合逻辑1的剩余部分(组合逻辑1A)与新合并出的组合逻辑(组合逻辑1B+组合逻辑2)的复杂度更加均衡,以此便可以提高整个时序逻辑的时间性能。例如,我们需要对一个数X进行如下操作,先加上常数17,然后再按位取反,然后再减去常数37,最后再乘以常数23并得到结果Y。考虑到整个运算过程比较复杂,因此可以分两步来完成整个求解过程,下图便是一种方案:

仔细观察上图,可以发现后两个寄存器之间的组合逻辑处理了过多的内容,尤其是乘法的处理更是需要消耗更多的时间,所以这将成为整个时序逻辑的短板,限制整个电路的时间性能。若加法、取反、减法操作的组合逻辑延迟均为T,乘法的为3T,那么上述电路的“短板”时间延迟达到5T,而另一块板的时间延迟仅为T,这是非常不合理的。因此,为了提高整个时序逻辑的时间性能,采用分布调整的方法对上述原理电路进行修改,得到新的方案如下图所示:

新的方案中,第一部分组合逻辑的时间延迟为3T,第二部分的组合逻辑时间延迟也是3T,因此整个方案的组合逻辑分配非常均衡,整个时序电路“短板”的时间延迟仅为3T,比之前的方案多出了2T的余量,这便是分布调整方法对于时域优化的作用。
最后需要说明一点,分布调整不同于逻辑拆分,因为它并没有改变原有组合逻辑的块数,而逻辑拆分则会增加原有组合逻辑的块数,并且同时会增加空间方面的开销。关于逻辑拆分的应用将会在【时空变换之空间换时间】小节中详细介绍。
思路转换
要解决一个问题,方法有很多,这其中必然有一些方法更巧妙或在某一方面更巧妙一些,也必然有一些方法更啰嗦或在某一方面更啰嗦一些。由于每个FPGA开发者的水平和经验都有所不同,因此在解决FPGA设计问题时,所能想到的解决思路也会有所不同。那么,当你在进行FPGA设计的时候,你所想出的思路将受限于个人的经验、水平以及思考时间,一般来说很难到达最优或者在某方面最优。很多时候,只要你所想到的方案能够算得上次优的,已经算是很不错了。而思路这个东西是宏观的,它决定了整个FPGA设计大的框架和方向,一旦这个东西确定了,那么最终逻辑电路的时空特性也就大致定了型,即便后续我们做了充分的逻辑化简、结构调整、分布调整等工作,也难对最终逻辑电路的时空特性产生较大的影响。因此,当我们的FPGA设计遭遇了瓶颈,换个解决思路往往能收到豁然开朗的奇效,有时候可能提升了时域性能,有时候可能提升了空域性能,有时候甚至能够对时空两方面的性能都带来大幅的提升,当然,有时候也可能会对其中一方面或者两方面都造成不好的影响。
例如,乘法的实现就有很多种思路:使用内嵌的DSP资源实现,这种思路的时域性能较好,但DSP资源一般比较紧俏;使用寄存器、查找表等逻辑资源实现,这种思路的时域性能较差,并且对逻辑资源的消耗也不小;使用BLOCK RAM建立乘法口诀表来实现,这种思路的时域性能也较好,但是对于位宽比较大的乘法,该口诀表可能会消耗太多的存储空间;使用一个累加器,将A乘以B分解为A+A+……+A(B个A),这种思路很省资源,但是时间上面却消耗太大;如果乘法中乘数是固定的,那么则可以利用这一特性并结合移位运算来轻松实现乘法,这样的话对时域和空域都会比较好;如果重新分析后发现其实这里仅需要一个加法运算即可,那么整个逻辑的时空性能将得到进一步提升;等等。
下面,给出一个思路转换的示例——提前进位多级累加器:
提前进位法提高多级累加器的工作频率
一般在设计多级累加器时,我们大多将代码写成如下形式。以一个3级累加器为例,累加器A的累加范围为0134,累加器B的累加范围为070,累加器C的范围为0~241。
-- VHDL example
signal A, nextA, B, nextB, C, nextC : std_logic_vector(7 downto 0);
process (clk)
begin
if(clk'event and clk = '1')then
if (rst = '1') then
A <= X"00";
B <= X"00";
C <= X"00";
else
A <= nextA;
B <= nextB;
C <= nextC;
end if;
end if;
end process;
process (A, B, C)
begin
nextA <= A;
nextB <= B;
nextC <= C;
if(A = 134)then
nextA <= X"00";
if(B = 70)then
nextB <= X"00";
if(C = 241)then
nextC <= X"00";
else
nextC <= C + 1;
end if;
else
nextB <= B + 1;
end if;
else
nextA <= A + 1;
end if;
end process;
// Verilog example
reg [7:0] A, nextA, B, nextB, C, nextC;
always@(posedge clk)
begin
if(rst)
begin
A <= 8'd0;
B <= 8'd0;
C <= 8'd0;
end
else
begin
A <= nextA;
B <= nextB;
C <= nextC;
end
end
always@(A, B, C)
begin
nextA = A;
nextB = B;
nextC = C;
if(A == 8'd134)
begin
nextA = 8'd0;
if(B == 8'70)
begin
nextB = 8'd0;
if(C == 241)
begin
nextC = 8'd0;
end
else
begin
nextC = C + 1'b1;
end
end
else
begin
nextB = B + 1'b1;
end
end
else
begin
nextA = A + 1'b1;
end
end
这是一个比较正规的写法,思路清晰且容易理解,在绝大多数情况下能够胜任。不过这里有一个问题,那就是存在一条会成为整个设计瓶颈的关键时序路径。
我们仔细分析一下代码就会发现,整个代码只有三个(其实是三组)寄存器,即A、B、C,它们的值每一个时钟周期都会更新。
A的下一拍值nextA,仅仅由关于A的组合逻辑决定;
B的下一拍值nextB,由A和B的组合逻辑决定;
C的下一拍值nextC,由A、B和C的组合逻辑决定;
当A等于134,B等于70的时候,输出一个nextC需要经历最复杂的组合逻辑,这个逻辑可能是这样的(不同的编译器综合结果会有差异,这里仅给出一个示意图):

从上图可以看出来,产生nextC所需要的最长组合逻辑时延很可能为1个8位比较器加3个8位2路选择器的延迟,或者是一个8位加法器和3个8位2路选择器的延迟。如果考虑了布局布线,那么情况可能会更加糟糕。并且随着累加数的位宽进一步扩大或者累加级数的进一步增多,这个组合逻辑的时延将会限制到累加器的性能,从而使其不能达到我们所需要的累加计数速度。
为了能够提高多级累加器的工作频率,我们需要改变上面这种结构,从而使得当A等于134,B等于70时,nextC不再依赖于如此复杂的组合逻辑。
分析一下A到B的进位规则可以发现,与其在A等于134时才考虑nextB的值,不如在A等于133时就给出一个1位的进位信号,这样的话当A等于134时,nextB就可以通过判断这个进位信号来选择自己的值。于是代码改写如下:
-- VHDL example
signal A, nextA, B, nextB, C, nextC : std_logic_vector(7 downto 0);
signal carryA, nextCarryA, carryB, nextCarryB, carryC, nextCarryC : std_logic;
process (clk)
begin
if(clk'event and clk = '1')then
if (rst = '1') then
A <= X"00";
B <= X"00";
C <= X"00";
carryA <= '0';
carryB <= '0';
carryC <= '0';
else
A <= nextA;
B <= nextB;
C <= nextC;
carryA <= nextCarryA;
carryB <= nextCarryB;
carryC <= nextCarryC;
end if;
end if;
end process;
process (A, B, C, carryA, carryB, carryC)
--following are carrys
if(A = 133)then
nextCarryA <= '1';
else
nextCarryA <= '0';
end if;
if(B = 70)then
nextCarryB <= '1';
else
nextCarryB <= '0';
end if;
if(C = 241)then
nextCarryC <= '1';
else
nextCarryC <= '0';
end if;
//following are counts
if(carryA = '1')then
nextA <= X"00";
else
nextA <= A + '1';
end if;
if(carryA = '1')then
if(carryB = '1')then
nextB <= X"00";
else
nextB <= B + 1;
end if;
else
nextB <= B;
end if;
if(carryA = '1' and carryB = '1')then
if(carryC = '1')then
nextC <= X"00";
else
nextC <= C + 1;
end if;
else
nextC <= C;
end if;
end process;
// Verilog example
reg [7:0] A, nextA, B, nextB, C, nextC;
reg carryA, nextCarryA, carryB, nextCarryB, carryC, nextCarryC;
always@(posedge clk)
begin
if(rst)
begin
A <= 8'd0;
B <= 8'd0;
C <= 8'd0;
carryA <= 1'b0;
carryB <= 1'b0;
carryC <= 1'b0;
end
else
begin
A <= nextA;
B <= nextB;
C <= nextC;
carryA <= nextCarryA;
carryB <= nextCarryB;
carryC <= nextCarryC;
end
end
always@(A, B, C, carryA, carryB, carryC)
begin
//following are carrys
if(A == 8'd133)
begin
nextCarryA = 1'b1;
end
else
begin
nextCarryA = 1'b0;
end
if(B == 8'd70)
begin
nextCarryB = 1'b1;
end
else
begin
nextCarryB = 1'b0;
end
if(C == 8'd241)
begin
nextCarryC = 1'b1;
end
else
begin
nextCarryC = 1'b0;
end
//following are counts
if(carryA == 1'b1)
begin
nextA = 8'h0;
end
else
begin
nextA = A + 1'b1;
end
if(carryA == 1'b1)
begin
if(carryB == 1'b1)
begin
nextB = 8'h0;
end
else
begin
nextB = B + 1'b1;
end
end
else
begin
nextB = B;
end
if(carryA == 1'b1 && carryB == 1'b1)
begin
if(carryC == 1'b1)
begin
nextC = 8'h0;
end
else
begin
nextC = C + 1'b1;
end
end
else
begin
nextC = C;
end
end
需要说明的一点是:carryB和carryC的产生原理和carryA不一样,原因是B和C每变化一次都是多时钟周期的,所以不能像carryA一样应用提前进位的方法来产生,不过这并不会拖累多级累加器的性能,因为carryB和carryC都是寄存器,因此它们都起到了阻止前级组合逻辑延迟传递到nextB和nextC的作用。
现在我们再仔细分析一下代码里的寄存器。
carryA的下一拍值nextCarryA,仅仅由A的组合逻辑决定;
carryB的下一拍值nextCarryB,仅仅由B的组合逻辑决定;
carryC的下一拍值nextCarryC,仅仅由C的组合逻辑决定;
A的下一拍值nextA,由carryA和A的组合逻辑决定;
B的下一拍值nextB,由carryA、carryB和B的组合逻辑决定;
C的下一拍值nextC,由carryA、carryB、carryC和C的组合逻辑决定;
由此可见,nextC仍为最复杂的组合逻辑,但当A等于134,B等于70的时候,nextC的逻辑可能是这样的(不同的编译器综合结果会有差异,这里仅给出一个示意图):(&&改为&)

很明显,这个nextC的组合逻辑要明显简单的多,并且没有了复杂的比较器,因此,在一个庞大的设计中,这样的组合逻辑在布局布线后更加容易达到高速的时钟频率要求。
布局调整
当编译器将我们编写的HDL代码转换为门级网表后,编译过程并没有结束,只有将门级网表所代表的内容真正映射到FPGA芯片内部后,FPGA芯片才会具有预期的逻辑功能。所以,一块组合逻辑的时间延迟不仅仅取决于各个基本组合逻辑单元的门延迟,同时也会受到连接各个基本组合逻辑单元的布线的线延迟,有些时候线延迟甚至对组合逻辑的时间延迟影响还要大一些。因此,通过直接调整编译器布局布线后的结果,人为的将某一块组合逻辑所包含的各个基本组合逻辑门排列得更紧凑一些,便可以达到提高FPGA设计时间性能的目的。
当然了,人工的布局调整方法,根据FPGA芯片的集成开发环境不同,具体操作方式也不同。不过这种调整方式操作复杂,并且不具有继承性,因此一般较少采用,更为普遍的一种间接进行布局调整的方法是采用时序约束的方式来指导编译器进行布局、布线,从而达到较好的时间性能,具体的内容请参见本书的【时序分析篇】。