优先队列与堆

优先队列与堆

一 优先队列

1.1 定义

在很多应用中，我们通常需要按照优先级情况对待处理对象进行处理，比如首先处理优先级最高的对象，然后处理次高的对象。最简单的一个例子就是，在手机上玩游戏的时候，如果有来电，那么系统应该优先处理打进来的电话。

在这种情况下，我们的数据结构应该提供两个最基本的操作，一个是返回最高优先级对象，一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue) 。

优先级队列和通常的栈和队列一样，只不过里面的每一个元素都有一个”优先级”，在处理的时候，首先处理优先级最高的。如果两个元素具有相同的优先级，则按照他们插入到队列中的先后顺序处理。

1.2 API

优先队列最重要的操作就是删除最大元素和插入元素
删除最大元素的方法名为 delMax()，插入元素的方法名为 Insert()。定义类 MaxPQ 的API如下：


类似的，我们会在适当的地方使用另一个类 MinPQ。它和 MaxPQ 类似，只是含有一个 delMin() 方法来删除并返回队列中键值最小的那个元素。

1.3 实现

优先级队列可以通过数组，链表，堆或者其他数据结构实现。

最简单的优先级队列可以通过有序、无序数组来实现，当要获取最大值的时候，对数组进行查找返回即可。

• 如果使用无序数组，那么每一次插入的时候，直接在数组末尾插入即可，时间复杂度为 O(1) O ( 1 ) 。但是如果要获取最大值，或者返回最小值的话，则需要进行查找，这时时间复杂度为 O(N) O ( N ) 。
• 如果使用有序数组，那么每一次插入的时候，通过插入排序将元素放到正确的位置，时间复杂度为 O(N) O ( N ) ，但是如果要获取最大值的话，由于数组已经有序，直接返回数组末尾的元素即可，所以时间复杂度为 O(1) O ( 1 ) .

采用普通的数组或者链表实现，无法使得插入和排序都达到比较好的时间复杂度，在这些初级实现中，插入元素和删除最大元素这两个操作之一在最坏情况下需要线性时间来完成 (如表2.4.3所示)。

所以我们需要采用新的数据结构来实现。下面要讨论的基于数据结构堆(heap)的实现能够保证这两种操作都能更快执行。

二 堆

数据结构二叉堆能够很好地实现优先队列的基本操作。
在二叉堆的数组中，每个元素都要保证大于等于另两个特定位置的元素。

2.1 定义

当一棵二叉树的每个结点都大于等于它的两个子结点时，它被称为堆有序。

根节点是堆有序的二叉树中的最大节点。

2.2 表示

可以使用完全二叉树表示二叉堆(以下简称堆)，而无需使用指针。
将二叉树的结点按照层级顺序放入数组中，根节点在位置1（不使用数组的第一个位置），它的子节点在位置2和3，子节点的子节点则分别在位置4、5、6、7，以此类推。

从二叉堆中，我们可以得出：

• 元素 k 的父节点的位置为 ⌊k/2⌋ ⌊ k / 2 ⌋
• 元素 k 的子节点所在的位置为 2k 2 k 和 2k+1 2 k + 1
• 一棵大小为 N N 的完全二叉树的高度为 ⌊lgN⌋ ⌊ l g N ⌋

这样在不使用指针的情况下，也可直接通过计算数组的索引完成结点的上下移动。

2.3 堆的有序化

用长度为 N+1 的数组 pq[] 来表示一个大小为 N 的堆。
注意：不使用 pq[0]，堆元素放在 pq[1] 至 pq[N] 中

堆的有序化：
swim()：当某个结点的优先级上升（例如在堆底加入一个新的元素）时，我们需要由下至上恢复堆的顺序。
sink()：当某个结点的优先级下降（例如将根节点替换为一个较小的元素）时，我们需要由上至下恢复堆的顺序。
现在就来看这两种操作。

1、由下至上的堆有序化（上浮）
当一个结点太大时，它需要 浮（swim）到堆的更高层，直到遇到了一个更大的父节点。

我们只需要将该元素 k 和其父元素 k/2 进行比较，如果比父元素大，则交换，然后迭代一直到比父元素小为止。

//结点比父节点大，上浮
public void Swim(int k)
{
        while (k > 1 && pq[k] > pq[k / 2])   //如果元素比其父元素大，则交换
        {
            Swap(pq, k, k / 2);
            k = k / 2;
        }
}

2、由上至下的堆有序化（下沉）
当一个结点太小时，它需要 沉（sink）到堆的更低层，直到它的子节点都比它更小或者到达了堆的底部。

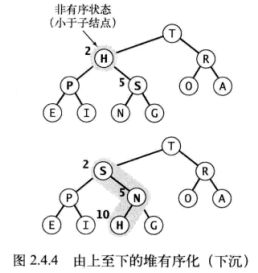
我们只需要将该元素 和 它的两个子节点中的较大者 进行比较，如果比较大者小，则交换。

//结点比子节点小，下沉
public void Sink(int k)
{
        while (2 * k <= N)
        {
            int j = 2 * k;
            if (pq[j] < pq[j + 1]) j++;    //选择左右子节点中的较大者
            if (pq[k] > pq[j]) break;      //如果父节点比这个较大者还大，表示满足要求，退出
            Swap(pq, k, j);                //否则，与子节点进行交换
            k = j;
        }
}

2.4 基于堆的优先队列

swim() 和 sink() 有序化是实现基于堆的优先队列API的基础。
优先队列最重要的操作就是删除最大元素和插入元素

1、插入元素
将新元素加到数组末尾，并让这个新元素上浮 swim() 到合适的位置。

//将N加一并把新元素添加在数组最后，然后用swim()恢复堆的秩序
public void insert(int num){
        pq[++N] = num;
        Swim(N);
}

2、删除最大元素
从数组顶端删去最大的元素，并将数组的最后一个元素放到顶端，再让该元素下沉 sink() 到合适的位置。

//从pq[1]中得到最大元素，然后将pq[N]移动到pq[1]，将N减一并用sink()恢复堆的秩序
public int delMax(){
        int max = pq[1];
        Swap(pq, 1, N--);
        //pq[N + 1] = null;  将不再使用的pq[N+1]设为null，以便系统回收它所占用的空间
        Sink(1);
        return max;
}

3、基于堆的优先队列

对于一个含有N个元素的基于堆的优先队列，
插入元素的操作需要不超过 lgN+1 l g N + 1 次比较
删除最大元素的操作需要不超过 2lgN 2 l g N 次比较

两种操作都需要在根节点和堆底之间移动元素，而路径的长度不超过 lgN。对于路径上的每个节点，删除最大元素需要两次比较(除了堆底元素)，一次用来找出子节点中的较大者，一次用来确定该子节点是否需要上浮。