CUDA学习笔记（LESSON4）——GPU基本算法（Part II）

CUDA系列笔记

CUDA学习笔记（LESSON1/2）——架构、通信模式与GPU硬件

CUDA学习笔记（LESSON3）——GPU基本算法（Part I）

CUDA学习笔记（LESSON4）——GPU基本算法（Part II）

CUDA学习笔记（LESSON5）——GPU优化

CUDA学习笔记（LESSON7）——常用优化策略&动态并行化

---

GPU基本算法（Part II）

Scan应用

压缩（Compact）

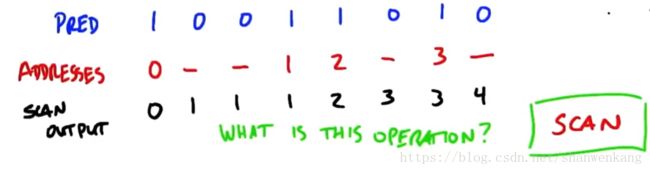
Compact实际上是在一组数据中把我们需要的部分挑出来的一种方法，具体步骤如下：第一步对数据进行一个predicate，将我们需要的数据标为true，其他的数据标为false；第二步开辟一个数组与原数组对应，将prdicate结果为true对应的位置存入1，其他的存入0；第三步，对这个数组进行exclusive scan，就可以得到这些数据在新数组中的地址了，我们把这个地址叫做scatter address；第四步就是将输入元素映射到输出元素中。

分配（Allocate）

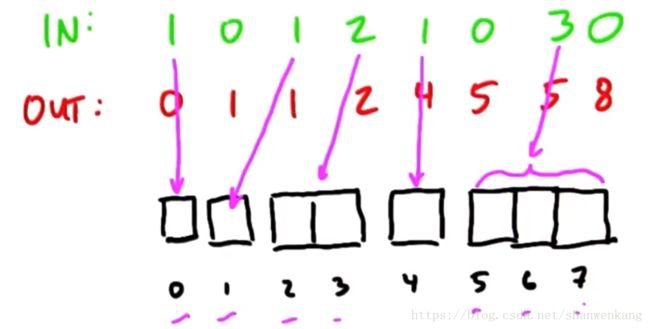
Allocate是类似compact的操作，其中输出的项数可以动态地从输入项计算出。例如下面这个例子，输入的元素个数不固定，然后需要将其映射到输出，那么这种情况我们怎么获取scatter address呢？与compact不同的就是在做predicate的时候我们不再用0和1表示，而是写出输入元素的个数，之后进行exclusive scan，这样我们就能得到地址的值了。

 

稀疏矩阵向量乘法（SpMv）

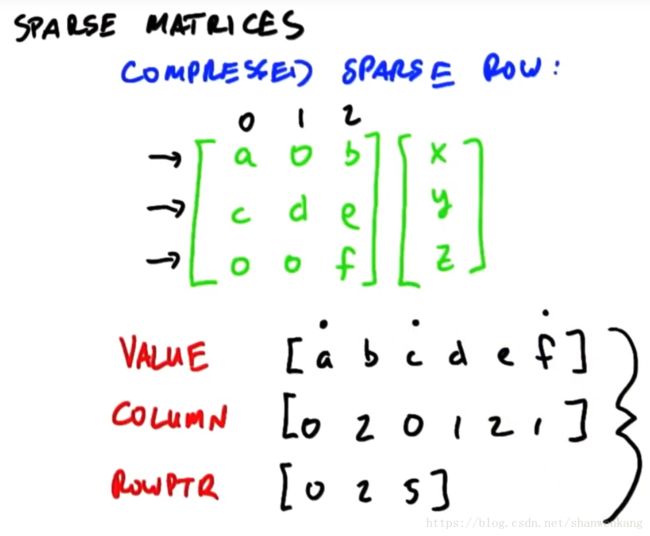
当一个矩阵0的个数远大于有值位置的个数的时候，我们把这个矩阵称为稀疏矩阵，对于稀疏矩阵与向量相乘，效率是非常低的，因为会有大量的0*0，而这种计算是没有意义的。所以我们需要一种更加高效的算法。表示稀疏矩阵向量的方法叫做压缩稀疏行（compressed sparse row），我们对于一个稀疏矩阵用三个向量表示：value、column与rowptr。其中value是按顺序写下矩阵中的每个元素，column是记录下value中的值分别对应哪一列，rowptr记录下每一行开始元素对应其在value中的索引。

下面让我们来看怎么用CSR来进行稀疏矩阵向量乘法，首先我们根据value与rowptr的值生成分段的元素，其次我们根据column来计算元素对应与向量中哪个元素相乘，进行乘法运算得到一个新的结果，在对这个结果进行分段扫描（segmented scan）就可以得到最终的结果了。在这个过程中我们可以看出scan仍是计算最主要的部分，利用并行计算可以大大地加速。

 

排序（Sort）

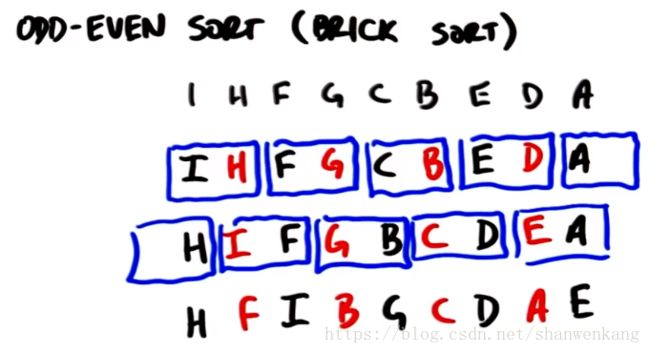
奇偶排序（odd-even sort/brick sort）

在并行世界中的算法跟串行世界中的算法还是有一些区别的，在并行世界中最简单的算法就是奇偶排序（odd-even sort/brick sort）。这种算法不断交换相邻元素的位置最终使元素达到有序，这种相邻位置元素的交换跟bubble sort很像，因此这种算法的复杂度并不是很让人满意，step complexity为O（n），work complexity为O（n^2）。

 

归并排序

如果我们想有什么串行算法最适合并行计算的，那无疑就是归并排序了，但是如果我们仔细想想就会发现归并排序中也存在并行不是特别好的部分，下面我们来解决如何将这部分用并行计算来表示。对于一个数据量很大的排序（如下图），我们可以把它分为三个部分：第一个部分是由许多个小的排序构成，我们往往将每一个任务分给它一个线程，这个任务就足够得以解决。第二部分与第一部分有一个临界值，是shared memory的大小值，因为我们在之前学到如果把需要频繁访问的数据放到shared memory中可以提高效率，因此对于第一部分数据量小的时候我们可以把数据全放进shared memory中。而这部分数据我们往往不采用归并排序，而是有更高效的排序网络；然后到第二部分，这一部分数据量多了起来，一个排序任务的数据量比较多，因此我们将每个任务分给一个block处理，因此这个阶段在运行的SM是与任务数相当的；到了第三个阶段我们每次排序的数据量非常多，而任务数很少，这种情况我们将一个大任务分成许多个小任务，交由不同的SM处理，这样子我们就让每一个SM都有任务可以做，大大提高了GPU的效率。

第二部分

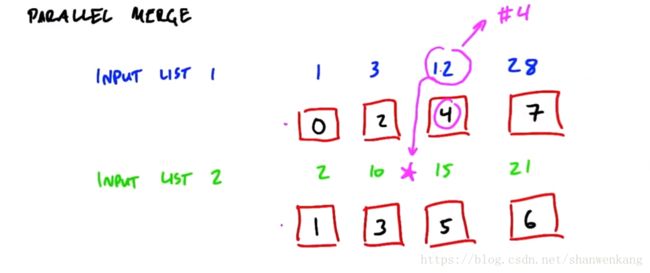
我们先来看第二阶段归并排序的并行版本改进。我们知道对于两个有序序列要合成一个有序序列需要一个串行处理器，在两个有序序列的头部挑一个最小的元素作为输出元素，如此反复，知道两个有序序列全部读完，这时候我们得到的输出序列就是一个有序序列。

我们可以看出这种串行算法很显然不适合并行计算，对于较长的序列，需要很久的处理时间，那我们怎么讲其分解为并行的任务呢？答案就是我们对于每一个元素都算出它在输出序列中的地址，然后由输入到输出映射即可。那么如何得到这个地址呢？我们知道这个地址是由当前元素在本序列的位置加上在另外一个序列中按大小排序的位置相加得到的。例如下图中的12在本序列中的索引是2，而将这个数放到序列2中按大小排序得到的位置索引也是2，因此这个元素在输出序列中的位置索引是4。那么这个数值应该如何计算呢？首先这个元素在自己序列的索引很容易知道，那么我们需要知道的就是它在另一个序列中的位置，计算方法就是把这个元素放到另一个序列中进行二分搜索，就能得到第二个位置索引了。而二分搜索的过程就可以采用并行计算了。

第三部分

我们知道当数据量很多，任务数很少的时候，如果我们还是让一个block负责一个任务的话，就会有很多SM处于空闲状态，为了解决这个问题我们可以将大任务分解成很多小任务。首先我们在大序列中取出一些元素称为（splitter），然后可以利用上述的方法对其进行排序，也可以求出当前元素在另外一个序列中的位置，这样我们就将本来很大序列分为了许多小块，为了使最终排序的高效性，我们可以将splitter的间隔限制在一定的范围，以保证最终排序的元素都能放入shared memory中。当我们将序列分为许多区间以后，我们就可以对其进行排序了。例如FC之间，我们已经确定了F与C的位置，那么输出序列中FC之间的元素都在下图的红色区域中，因此我们只需要对这两个子序列进行排序就可以得到最终输出序列FC之前的元素顺序。这样我们就将本来两个大的有序序列分为了很多个成对的小有序序列，之后我们采用第二部分的方法就可以对子任务进行计算了。

 

第一部分

在这一部分我们需要考虑与输入无关的算法，也就是不管输入数据是以什么顺序排列的，其计算复杂度是一样的。我们把这一部分称为排序网络（Sorting network），而最常用的算法就是双调排序（Bitonic sort），我们把序列先上升后下降（或先下降后上升的序列）称为双调序列，我们将双调序列内部对应元素进行比较，将大的元素放在一个数组中，小的元素放在另一个数组中，我们可以得到两个双调序列，而且第一个双调序列中的元素全部大于第二个双调序列中的元素。这样重复进行最终就能得到排序完成的序列了。而我们刚才谈的是对双调序列的排序，那么对于任意一个普通的序列我们如何生成它的双调序列的，过程就是上述的逆过程，从相邻的两个元素开始生成小的双调序列，然后对于小双调序列排序，得到有序的小序列，将两个小的有序序列以相反的方向拼接在一起就得到一个大的双调序列了，这样重复进行最终就能得到原序列对应的双调序列了。之前浙大考核的时候我也做过双调序列更详细的学习，具体内容：戳我。对于这个过程在GPU的实现，我们只需要给每个元素分配一个线程来保存比较后元素的值，这样每次进行一组比较后我们进行一次同步就可以开始下一次比较了。

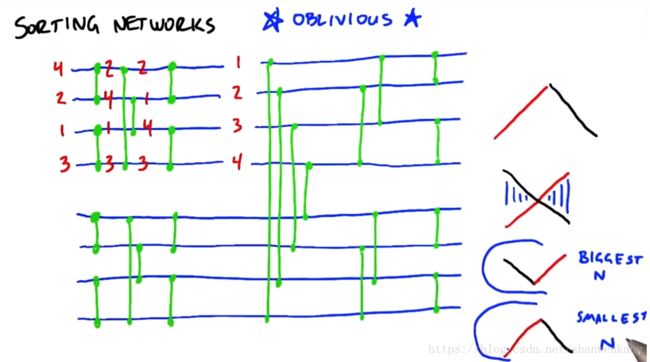如果能将输入元素全都放进shared memory中，那么排序网络是一种非常有效的方法，需要注意的是双调排序并不是排序网络的唯一算法，还有奇偶归并排序（odd-even merge sort）等算法也可以用作排序网络。

基数排序（Radix sort）

最后要讲的是在GPU中效率最高的方法：基数排序。到目前为止我们讲的排序方法都是比较排序，也就是交换元素的顺序，而比较排序是依赖于数字位置的比较方法。我们将一个数用二进制位来表示，从最低位到最高位开始扫描，把每一位是0的放在上面，是1的放在下面，之后开始扫描第二位，重复这个过程直到最高位扫描结束，得到的序列就是排序好的序列。这个算法在GPU上运行流畅的原因有两个，第一个就是其优越的复杂度，为O（kn），k是表示一个数的比特位。第二个就是每一次排序过程都可以用我们之前学过的算法表示，也就是compact，我们对一个特定的比特位进行扫描就能得到元素的在新序列中的地址索引。通过每次扫描多个比特位我们还能提高这个算法的效率。

快速排序

快速排序也是我们在串行世界中用的很多的算法，我们选用一个参考元素（pivot element），之后把元素分为小于该元素，等于该元素，大于该元素的三个数组，再分别对这三个数组用同样的方法重复进行，直到排序完毕。

在并行实现的时候我们可以通过distribute、map、compact的操作将原数组分段，然后再段内开启另外的线程来达到与递归类似的效果。