智能优化算法：绯鲵鲣优化算法-附代码

智能优化算法：绯鲵鲣优化算法-附代码

摘要：绯鲵鲣优化算法[1]（Yellow Saddle Goatfish Algorithm ，YSGA）是由 Erik Cuevas等于2018年提出的一种新型的仿生智能优化算法．该算法模拟绯鲵鲣群协作狩猎行为以实现对搜索空间的探索和开采，同时通过选定追逐者与拦截者的代理搜索学习机制以改善种群的个体多样性和算法的迭代寻优能力；鉴于该算法待调节参数少、迭代寻优效率高且易于实现等优点，将具有较好的可拓展改进空间和应用前景。

1.算法原理

YSGA 算法是锁定狩猎区域后，通过 K-means方法将绯鲵鲣种群划分为 k 个相互独立的簇以实现空间邻域内的并行搜索，并使绯鲵鲣在探索空间内扮演两种搜索代理角色，即追击鱼和拦截鱼以执行不同的搜索路径操作。在狩猎过程中，因鱼群随机游走可发生角色互换机制，若狩猎区域被过度开采，绯鲵鲣鱼群将执行区域更新策略以寻找新的捕食区域继续狩猎。根据绯鲵鲣群体协作狩猎行为的特点，YSGA 算法通过初始化、追击鱼、拦截鱼、角色互换与更改区域 5 种不同行为模式的数学化描述以实现问题的优化求解。

1.1初始化阶段

种 群 $P=\{p_1,p_2,...,p_n\}$在 $n$ 维 搜 索 空 间$[b^{high},b^{low}]$内随机生成且均匀分布，并按式(1)进行初始化。
$$p_i^j=rand.(b_j^{high}-b_j^{low})+b_j^{low},i=1,2,...,m;j=1,2,...,n\text{\hspace{1em}(1)}$$
其中，$m$为种群规模的大小，$p_i$为决策变量向量$p_i=p_i^1,p_i^2,...,p_i^n$,$rand$是[0,1]中的随机数。

YSGA 模型运用 K-means 算法进行聚类分析，将种群$p$划分为$k$个相互独立的簇$\{c_1,c_2,...,c_k\}$ ，通过计算$k$个簇中的每个决策变量与该簇中心的欧氏距离之和来定义该算法的适应度值，以表示捕获猎物的成功率，具体记为:
$$E(C)=\sum _{i=1}^{k}e(c_l)\text{\hspace{1em}(2)}$$

$$e(c_l)=\sum _{p_gϵc_l}||p_g-u_l||\text{\hspace{1em}(3)}$$

其中$e(c_l)$表示每个簇$c_l$ 的均值$u_l$与簇中每个决策变量之间的欧氏距离,$g=1,2,...,h;l=1,2,...,k$。

1.2追击鱼路径

每个簇中适应度值较高的绯鲵鲣被暂定为该区域的追击鱼以引领捕猎，在搜索区域内利用列维飞行模型产生随机移动以寻找猎物的藏身之处，其位置更新表达式为
$${\Phi }_l^{t+1}={\Phi }_l^t+S\text{\hspace{1em}(4)}$$

$$S=\alpha \oplus Levy(\beta )\sim \alpha (\frac{u}{|v{|}^{1/\beta }})({\Phi }_l^t-{\Phi }_{best}^t)\text{\hspace{1em}(5)}$$

其中，${\Phi }_l^t$表示追击鱼当前的位置，$S$为列维飞行模型通过列维分布生成的随机步距；参数$\alpha$ 为步长控制因子且$\alpha =1$ ，参数$\beta$ 称为 Lévy 指数且 $0<\beta \le 2$ ，参数 $u$ 和 $v$ 服从正态分布；${\Phi }_{best}^t$是当前所有集群中最佳追击鱼，其位置更新表达式为:
$${\Phi }_l^{t+1}={\Phi }_l^t+S^{\prime }\text{\hspace{1em}(6)}$$

$$S^{\prime }=\alpha (\frac{u}{|v{|}^{1/\beta }})\text{\hspace{1em}(7)}$$

其中， $S^{\prime }$ 为新定义的随机步距。

1.3拦截鱼路径

每个簇中确定追击鱼后，剩余的绯鲵鲣就成为拦截鱼对猎物实行包围策略以阻止其逃跑，并沿着螺旋路径围绕在此时试图捕食猎物的追击鱼周围，其位置更新表达式为 :
$${\phi }_g^{t+1}=D_g.e^{b\rho }.cos2\pi \rho +{\Phi }_l\text{\hspace{1em}(8)}$$
其中，$D_g$ 是干扰距离，即拦截鱼${\phi }_g^t$ 和追击鱼${\Phi }_l$ 在簇$c_l$ 中当前位置的距离，$\rho$是[0,1]中的随机数，$b$ 是一个常数且 $b=1$。

1.4 角色互换

在追捕猎物过程中，若簇中的拦截鱼比追击鱼距离猎物更近，即具有更高的适应度值，则意味着寻找到了更优的解决方案，在迭代 t+1 中执行角色互换机制以更新最佳追击鱼的位置。

1.5 更改区域

YSGA 模型所选狩猎区域一旦被完全开发，即通过猎杀锁定的狩猎区域内所有猎物，对簇中所有的绯鲵鲣将执行区域更新策略，具体数学描述如下：
$$p_g^{t+1}=\frac{{\Phi }_{best}+p_g^t}{2}\text{\hspace{1em}(9)}$$
其中，$p_g^{t+1}$ 是绯鲵鲣的新狩猎区域，$p_g^t$是当前簇中绯鲵鲣(追击鱼或拦截鱼)成员的位置， ${\Phi }_{best}$是目前为止所有簇中适应度值最高的最佳追击鱼，即问题的最优解。

2.算法流程

step1.设置YSGA模型参数
step2.初始化绯鲵鲣种群．
step3.计算初始绯鲵鲣群每条鱼的适应度值．将每条绯鲵鲣的适应度值并比较大小，确定最大者为全局最优的绯鲵鲣追逐者，并保存当前最优值所对应的参数．再将种群分为ｋ个集群，计算每个集群中绯鲵鲣的适应度值，确定每个集群的追逐者和拦截者．
step4.对两种不同的搜索个体进行路径操作．对追逐者使用 Ｌéｖｙ飞行机制进行路径操作，将α的递变函数作为Ｌéｖｙ飞行的步长控制因子，对最优追逐者的位置进行更新；对拦截者执行对数螺旋路径，更新拦截者的当前位置．
step5.最优追逐者的更新．鱼群中追逐者和拦截者每进行一次路径操作，便计算一次当前集群的适应度值：若有一条绯鲵鲣拦截者的适应度值大于已保存的最优追逐者，则用当前的拦截者替换最优追逐者，使其成为新的最优个体，并保存该最优追逐者所对应的 参数，否则仍保存原追逐者位置和最优值所对应的参数．
step6.搜索空间更新．根据step5所计算的追逐者的适应度值，若其适应度值没有提高，则增加
该区域的搜索次数，直至达到过度开采参数；当超过过度开采参数时，则变换搜索区域．
step7.判断YSGA算法是否满足终止条件，即判断当前迭 代次数t是否达到 最 大迭代次数：若达到最大，则输出最优的追逐者和最优值所对应的参数，反之迭代次数t加１，并跳转执行step3．

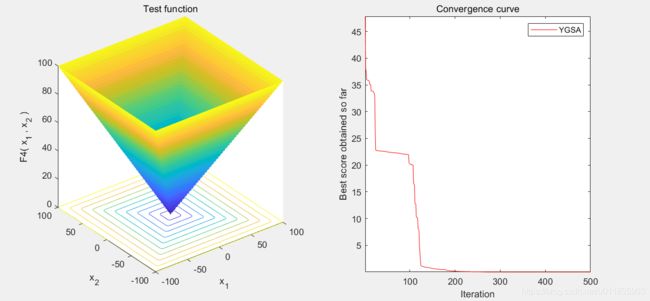
3.算法结果

4.参考文献

[1]Daniel Zaldívar,Bernardo Morales,Alma Rodríguez,Arturo Valdivia-G,Erik Cuevas,Marco Pérez-Cisneros. A novel bio-inspired optimization model based on Yellow Saddle Goatfish behavior[J]. BioSystems,2018,174.

[2]高雷阜,荣雪娇.融合递减策略与Fuch混沌机制的改进YSGA算法[J/OL].计算机科学与探索:1-16[2020-08-05].http://kns.cnki.net/kcms/detail/11.5602.TP.20200720.1328.008.html.

[3]高雷阜,荣雪娇.混合动态步长递变与局部混沌搜索的YSGA改进及其应用[J].辽宁师范大学学报(自然科学版),2019,42(01):16-24.

5.MATLAB代码

https://mianbaoduo.com/o/bread/Z5mUlJY=