遗传算法的简单讲解与matlab实现

1.简单介绍
略过遗传算法的发展史，本文直接讲解遗传算法的基本原理与实现。在生活中很多问题都可以转换为函数优化问题，大部分函数优化问题都可以写成求最大值或者最小值的形式，本文我们就用遗传算法来求一元函数最大值（最小值问题可以转化为最大值）。
遗传算法就是先产生出一定数量的个体，通过繁衍，交叉，变异产生更多的个体，对这些新的个体按一定条件进行筛选，始终留下一定数量的个体，如此反复，便能有最优解出现。
2.算法的实现
例：求函数 f(x)=x∗sin(3πx) f ( x ) = x ∗ s i n ( 3 π x ) 的最大值，定义域为 [−1,2] [ − 1 , 2 ] 。
1.参数设定

参数	设定值
编码类型	十进制数
种群大小	50
编码长度	5
最大迭代次数	100
适应度函数	f(x) f ( x )
交叉概率	0.8
变异概率	0.1

2.遗传过程
①.编码个体，当编码长度取5时，定义域被分为100000份， [0,99999] [ 0 , 99999 ] 对应着 [−1,2] [ − 1 , 2 ] 。
例如：基因 12345 12345 对应着 1234599999×[2−(−1)]+(−1) =0.6296 12345 99999 × [ 2 − ( − 1 ) ] + ( − 1 )   = 0.6296 。基因 00000 00000 代表x = −1 − 1 ， 99999 99999 代表 2 2 。
②.随机产生种群，包含50个个体。这些函数就是定义域上的点。

dna = randi([0, 9], [50, 5]); 

③.遗传时，产生0-1的随机数，当随机数小于交叉概率0.8时，就开始交叉。
交叉时 先选定两个个体，如13579和02468。
选择交叉断点，如2。
就产生新的个体13468与02579。
④.遗传时，产生0-1的随机数，当随机数小于变异概率0.1时，就开始变异。
变异时 先选定一个个体，如13579。
选择变异位置，如2。
产生一个0-9的随机数替代13579里面的3，
产生了新个体1?579。
⑤.现在的种群变成了，原始那一批+交叉的后代+变异的后代，对齐进行筛选。
先将现在的种群对应的 f(x) f ( x ) 解出，按从大到小的顺序排名。
⑥.开始筛选，产生一个随机0-1数，与 个体排名−1个体总数 个 体 排 名 − 1 个 体 总 数 进行比较，
产生的随机数小于 个体排名−1个体总数 个 体 排 名 − 1 个 体 总 数 是，淘汰这个个体。直到种群个体数变为50个。
⑦.如此循环100次，越来越接近最优解。

3.完整代码与效果
这是我学习的代码：

clear;  
clc;  
close all;  

f = @(x) x.*sin(3*pi*x) ;   % 函数表达式  
ezplot(f, [-1, 2]);             % 画出函数图像  

N = 50;                          % 种群上限  
ger = 100;                       % 迭代次数  
L = 5;                           % 基因长度  
pc = 0.8;                        % 交叉概率  
pm = 0.1;                        % 变异概率  
dco = [10000; 1000; 100; 10 ;1]; % 解码器  
dna = randi([0, 9], [N, L]);     % 基因  
hold on  
x = dna * dco / 99999 * 3-1;  % 对初始种群解码  
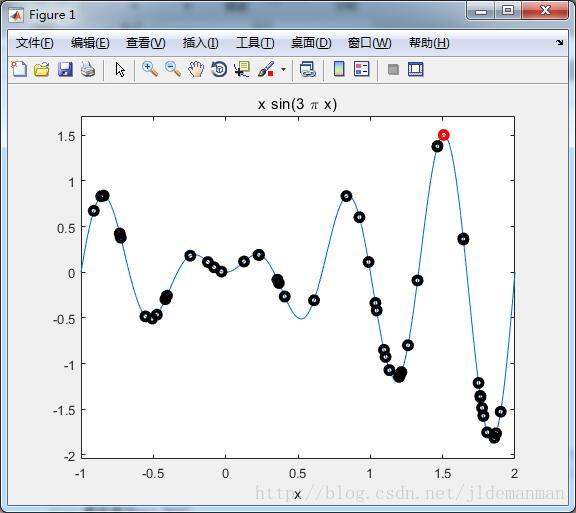
plot(x, f(x),'ko','linewidth',3) % 画出初始解的位置  

x1 = zeros(N, L);                % 初始化子代基因，提速用  
x2 = x1;                         % 同上  
x3 = x1;                         % 同上  
fi = zeros(N, 1);                % 初始化适应度，提速  

for epoch = 1: ger               % 进化代数为100  
    for i = 1: N                 % 交叉操作  
        if rand < pc             % 确定这个个体是否要交叉操作
           d = randi(N);            % 确定另一个交叉的个体
           m = dna(d,:);            % 确定另一个交叉的个体  
           d = randi(L-1);          % 确定交叉断点  
           x1(i,:) = [dna(i,1:d), m(d+1:L)];  % 新个体 1          
           x2(i,:) = [m(1:d), dna(i,d+1:L)];  % 新个体 2  
        end  
    end  
    x3 = dna;  
    for i = 1: N                           % 变异操作  
        if rand < pm  
            x3(i,randi(L)) = randi([0, 9]);  
        end  
    end  
    dna = [dna; x1; x2; x3];               % 合并新旧基因  
    fi = f(dna * dco / 99999 * 3-1);    % 计算适应度，容易理解  
    dna = [dna, fi];  
    dna = flipud(sortrows(dna, L + 1));    % 按照适应度进行排名  
    while size(dna, 1) > N                 % 自然选择  
        d = randi(size(dna, 1));           % 排名法  
        if rand < (d - 1) / size(dna, 1)   % 淘汰个体
            dna(d,:) = [];  
             fi(d,:) = [];  
        end  
    end  
    dna = dna(:, 1:L);  
    t(epoch)=max(fi);
end  
x = dna * dco / 99999 * 3-1;            % 对最终种群解码  
plot(x, f(x),'ro','linewidth',3)           % 画出最终解的位置  
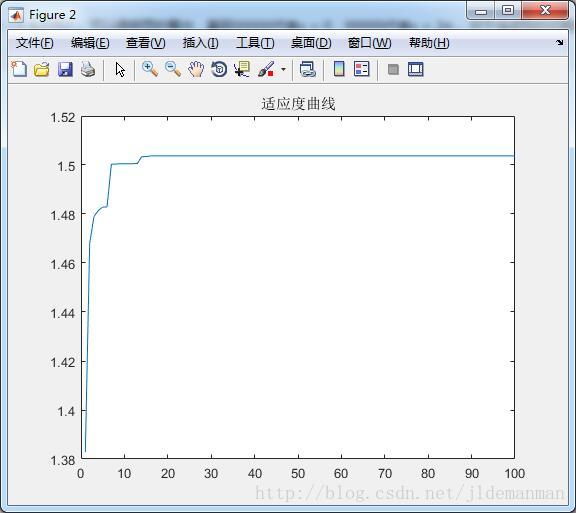
figure(2);plot(t);title('适应度曲线')
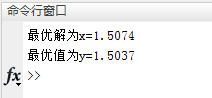
disp(['最优解为x=',num2str(x(1))]);  
disp(['最优值为y=',num2str(fi(1))]);