机器学习“傻瓜式”理解(13)混淆矩阵(评价分类结果)
之前的章节我们介绍了多种机器学习算法:
KNN->用于解决分类问题
线性回归->用于解决回归问题
逻辑回归->既可以解决分类问题,又可以解决回归问题
。。。
总体来说,我们机器学习的算法要解决的问题分为两大类,分别为:分类问题和回归问题。
从之前的内容来看,我们通过众多的机器学习算法得到的模型需要进行评估。
评价回归问题:MSE,MAE,RMSE,R^2(目前学习为止最好的评价算法)
评价分类问题:分类准确度(accuracy_score)
经验之谈,评价分类问题要比评价回归问题要复杂的多。
小引子:
我们搭建一个新冠肺炎检测系统,输如我们想要测试的人的数据进行检测,来根据得到的结果判断此人是否得了新冠肺炎。假设我们通过学习得到的模型预测的准确度为99.9%,
并且得有新冠肺炎的概率为0.1%,那么我们就算系统什么都不做,还是会有99.9%的预测准确度。
通过分析原因我们便得到,对于极度偏斜的数据(Skewed data),只使用分类准确度的方法来评估是远远不够的。
极度偏斜的数据:不同类型之间的样本的数量相差特别大,假设新冠肺炎感染概率1:10000
面对这种极度偏斜的数据,即使系统什么都不做,也可以达到十分大的准确度,此时我们可以通过混淆矩阵来进行进一步的分析。
对于各种概念,通过一张图进行相关介绍分析:

混淆矩阵代码实现:
'''Confusion Matrix'''
def TN(y_true,y_predict):
'''check'''
assert len(y_true) == len(y_predict)
return np.sum((y_true==0) & (y_predict==0))
def TP(y_true,y_predict):
'''check'''
assert len(y_true) == len(y_predict)
return np.sum((y_true==1) & (y_predict==1))
def FN(y_true,y_predict):
'''check'''
assert len(y_true) == len(y_predict)
return np.sum((y_true==1) & (y_predict==0))
def FP(y_true,y_predict):
'''check'''
assert len(y_true) == len(y_predict)
return np.sum((y_true==0) & (y_predict==1))
def confusion_matrix(y_true,y_predict):
return np.array([
[TN(y_true,y_predict),FP(y_true,y_predict)],
[FN(y_true,y_predict),TP(y_true,y_predict)]
])
def Precision(y_true,y_predict):
tp = TP(y_true,y_predict)
fp = FP(y_true,y_predict)
try:
return tp / (tp+fp)
except:
return 0.0
def Recall(y_true,y_predict):
fn = FN(y_true,y_predict)
tp = TP(y_true,y_predict)
try:
return tp / (tp + fn)
except:
return 0.0
评价分类结果的另外一种方式:F1 Score
在进行模型预测的过程中,通常会遇到下面的问题,例如我们需要单独考虑模型的精准率或者召回率,还可能出现我们需要同时考虑精准率和召回率两种指标,由此便产生了新的评价分类方式:F1_Score
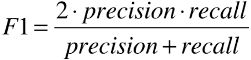
F1指的是精准率和召回率的调和平均值。
评价分类结果的另一种方式:P-R曲线
上面我们谈到的是我们可以通过精准率和召回率进行评价分类的结果,然而我们也可以通过调整阈值(threshold)来调整精准率和召回率的比重。
阈值越大,精准率提高,召回率降低。
阈值越小,精准率降低,召回率提高。
精准率和召回率是相互制约相互矛盾的两个变量,不能同时增高。
根据前面所讲到的精准率和召回率的定义,我们可以通过下面的几个案例进行相关分析:
假设我们所关注的事件还是为1
1.thershold = 0

精准率:4/5 = 0.8
召回率:4/6 = 0.67
2.threshold > 0
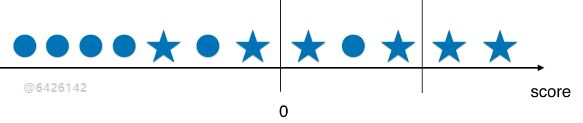
精准率:2/2 = 1
召回率:2/6 = 0.33
3.threshold < 0
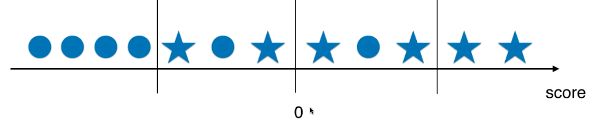
精准率:6/8 = 0.75
召回率:6/6 = 1
代码演示
#实例:调整阈值大小,进行调整精准率和召回率
import numpy as np
# 导入数据
from sklearn import datasets
# 导入模式数字集
digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()
# 为了更好的实验效果,将数据更改成极度偏斜的数据,解决二分类问题
y[digits.target == 9] = 1
y[digits.target !=9] = 0
# 划分训练数据集和测试数据集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 666)
# 进行逻辑回归预测
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X_train,y_train)
# 1.阈值threshold = 0
y_predict_1 = log_reg.predict(X_test)
# 得到混淆矩阵
from sklearn.metrics import confusion_matrix
con_m = confusion_matrix(y_test,y_predict_1)
print(con_m)
# 计算精准率
from sklearn.metrics import precision_score
p_s = precision_score(y_test,y_predict_1)
print(p_s)
# 计算召回率
from sklearn.metrics import recall_score
r_s = recall_score(y_test,y_predict_1)
print(r_s)
# 更改阈值
# 思路:基于决策函数decision_function方法,改变score的值,不在通过predict方法
# 阈值threshold = 5
decision_score = log_reg.dicision_function(X_test)
y_predict_5 = np.array(decision_score >= 5,dtype='int')
# decision_score >= -5便是将阈值更改为-5
con_m_5 = confusion_matrix(y_test,y_predict_5)
# 混淆矩阵:array([[404, 1],
# [ 21, 24]], dtype=int64)
precision_score(y_test,y_predict_5)
# 精准率:0.96
recall_score(y_test,y_predict_5)
# 召回率:0.5333333333333333
P-R曲线
代码部分只是通过for循环或者通过scikit也可以得出,不在此处演示,只讲解P-R曲线。
如图所示:
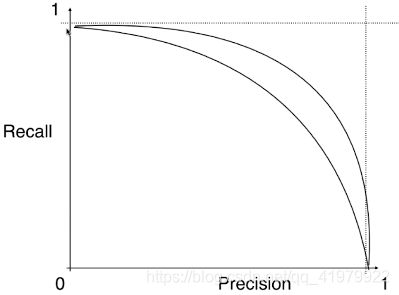
①这是两条P-R曲线
②图中曲线开始急剧下降的点便是精准率和召回率平衡的点。
③与坐标轴面积越大的模型越优。
④p-r曲线对于选择算法,超参数等等十分有好处,但是一般用的是roc曲线。
评价分类结果的另一种方式:ROC曲线
ROC(Receiver Operation Characteristic Curve)
通过一张图来详细的理清roc的种种概念。

封装代码:
def TPR(y_true,y_predict):
fn = FN(y_true,y_predict)
tp = TP(y_true,y_predict)
try:
return tp / (tp + fn)
except:
return 0.0
def FPR(y_true,y_predict):
fp = FP(y_true, y_predict)
tn = TN(y_true, y_predict)
try:
return fp / (fp + tn)
except:
return 0.0
混淆矩阵解决多分类问题
在具体介绍之前,首先介绍一种极其重要的思想:
在机器学习的过程中,我们不可避免的会出现很多的问题,但是这些问题并不一定全都来源于算法本身,我们要学会从样本数据的层面分析出现的问题,理解数据特征。
