拓展欧几里德
各位大佬,转载必须注明一下博客,自己写的不容易。/流眼泪
一 引例:
求两个数的gcd(a,b)=a和b两个数的最大公倍数?
-
短除法
-
更相减损法
-
辗转相除法
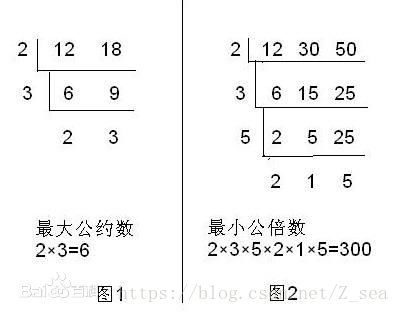
1、短除法:
百度百科——短除法
其实短除法的核心 唯一分解定理。我们要求的最大公约数,其实也是它本身的一部分因子。
复杂度 ![]()
注意:K=gcd(n,m)这个数的因子个数。
百度百科——唯一分解定理
我们演示一遍即可。
2、更相减损术:
百度百科——更相减损术
这个方法是来自我国数学:《九章算术》可以求最大公约数。
复杂度:O(N)
3、辗转相除法:(欧几里德)
百度百科——辗转相除法
复杂度: ![]()
图像 小部件
贴上代码:以上三种方法的使用。
#include
using namespace std;
void DC(){
int a=888,b=664,gcd=1;
while(1){
int flag=0;
for(int i=2;i<=min(a,b);i++){
if(a%i==0&&b%i==0){
gcd*=i;
a/=i,b/=i;
flag=1;
break;
}
}
if(flag==0){ //两者为互质
break;
}
}
printf("最大公约数:gcd(664,888)=%d\n",gcd);
printf("最小公倍数:lcm(664,888)=%d\n",gcd*a*b);
}
void XJ(){ //更相减损术
int a=888,b=664,temp=0,cnt=0;
while(a-b!=0){
//printf("%d %d %d\n",a,b,temp);
temp=a-b;
a=b;
b=temp;
if(a
二 拓展欧几里德:
上面提到了欧几里德,大家都看出来了,仅仅处理了一个小问题,就是计算一个最大公约数。
但是,这个计算公约数速度非常快,可以达到log级别的都是优质算法。
我们只是提及一下短除法和更相减损法,但是有时候面对小的数字,我们可以笔算一下这个最大公约数。
更多选择第一第二种。我们以后用的就是log级别的gcd来处理问题。
我们介绍一下通常拓展欧几里德给我们拓展了哪些问题。
-
求解 不定方程
-
求解 同余方程
-
求解 模的逆元
1.1 求解不定方程 引例
计算2809和6731的最小公倍数和最大公约数,并将两者的最大公约数表示成两者的线性组合?
——《离散数学》·张小峰 P25 第4小题。
1.2 、解题过程:
模拟辗转相除法:
6731=2809*2+1113
2809=1113*2+583
1113=583*1+530
583=530*1+53
530=53*10+0
上述过程就是辗转相除法。求得53是最大公因数。
然后我们需要求出 6731 和 2890 的关系。所以我们需要求出他们和最大公因数53的关系。
我们通过上面的式子倒推回去,不断表示两者中小的数字。
求特解过程:
53= 53 - 0
= 583 - 530
= 583 -(1113 - 583)=583*2 - 1113
=(2809 - 1113*2)*2-1113=2809*2 - 1113*5
= 2809*2 -(6731 - 2809*2)*5
= 12 * 2809 - 5 * 6731
通过倒推的过程大家其实意识到了,就是用上面的式子来操作,就好比辗转相除法的逆运算。
上面的推导过程就是拓展欧几里德求解 最小解 x, y 的过程了。
1.2.1、在模拟辗转相除法的过程中发现:
最开始的a和b:被 b 和 a%b 所代替。(这个就辗转相除的核心)
每次辗转的都是除数和余数交替相除的过程。
被除数变成除数: ![]()
除数变成余数: ![]()
所以在公式推导过程有:
![]()
1.2.2、在求特解的过程中发现:
上面的式子可能有问题!!!
问题出现在哪里呢,我们发现,其实a,b在变化的过程中,系数x,y也会对应发生变化。
我们推导一下它的变化过程吧!!!
![]()
![]()
![]()
上面的过程中,a和b都是相同的,我们可以去掉下标。
![]()
因为我们需要得到x1=****x2 y1=*****y2;
这样的关系。所以我们用到了待定系数法(听着很炫,其实就是表示为 **a+**b的形式).
把对应a和b当作变量,把对应的系数相等起来得到:
我们现在推导出来了的东西进行运用。
1.2.3、再次回顾辗转相除法:
我们通过这个辗转相除法得到的就是一个公约数。
然后我们可以通过两个数 a,b来推导出一组关系来表示这个gcd(a,b)
求解其中的系数关系x,y。
下面式子关键是弄清楚辗转相除法的核心进行推导:
1.2.4、关键思想:
不断用上一个式子的除数和余数来交替表示式子中的被除数 a 和除数 b
(你要是问我为什么会这样能弄出来最大公约数,我真不知道,那要问问欧几里德) \逃
a x1 + b y1 = gcd(a,b)
b x2 + ( a % b ) y2 = gcd( b , a % b )
………………………………
第n次辗转后——求到最大公约数时:
n *1 + 0 * 0 = gcd(a,b)
这个过程解释清楚了吧!!!这里挺难理解的,就是辗转到最后,
突然发现没有余数了,那么就说明这个 上一个式子的除数 n=gcd(a,b)
我们已经求出来了,并且我们能确保当前位置的 xn=1,yn=0;
我们刚才不是推导了吗?
x1,y1 是上一个式子,x2,y2代表是下一个式子。
我们不就是进行回溯过去不断用式子来表示 x1,y1。
最后回溯到最开始的 a,b不就是我们想要求出来的答案吗!!!
1.2.5、代码表示过程:
#include
int exgcd(int a,int b,int &x,int &y){//返回的是最大公约数.
//此时 a,b代表的是上一个式子的除数和余数
if(b==0){//余数为0
x=1;
y=0;
return a;
}
int r=exgcd(b,a%b,y,x);//递归求解gcd(a,b);
y=y-a/b*x;//不要在乎细节,这里就是x,y的值调换,公式还是那样.
return r; //别忘了这一句,不然得不到最大公约数
}
int main(){
int x,y,a=6731,b=2809;
int gcd=exgcd(a,b,x,y);
printf("%d = (%d)*%d + (%d)*%d",gcd,x,a,y,b);
}
1.2.6、运行结果:
1.3、再次回顾ax+by=c:
1.3.1、求特解:
上面说的,只能解决一个式子:那就是:ax+by=gcd(a,b)
大家思考一下,其实ax+by=c可能没有解。
那就是 c%gcd(a,b)!=0
这就是我们解决这个式子的第一步!!!
第一步:
通过c%gcd(a,b)==0来判断是否有通解。
第二步:
求解满足ax+by=c的一组特解
若有通解的情况下,代入上面的代码我们解出来的一个x0,y0只是符合ax+by=gcd(a,b)
但 不是我们题目要求的ax+by=c的方程的根。
聪明如你是否想到了????
因为判断通解的过程就说明这个c一定是gcd(a,b)倍数关系。
所以我们求解的过程可以弯曲一下。
已知:
![]()
凑一下:
![]()
再看看已知:我们就可以得出一组特解:
得出:
1.3.2、求多组整数解:
我们其实知道这样的二元一次方程组,可以有很多解。
那么我们怎么做才行呢????
一个字就是: 凑!!!!!!
我们想一下,其他解是怎样的形式!!!
![]() 其中(x1,y1是上面)
其中(x1,y1是上面)
为了保持左边的值等于右边,我们凑一下出来了;
???满足:在a*???+b*???=0;
那么我们用gcd(a,b)作分母,只要分子有另一方的倍数即可。
所以有:
一个词总结再好不过:彼消此长
1.3.3、求最小正整数解 :(x or y)
通过上面的此消彼长.
只要我们让x的不断减少,当减少到负数,那么上一次的x的必定是最小正整数解。
其实我们可以用for循环历遍。
不妨设:
只要满足:
![]()
后来发现这个最小正整数解不就是:
![]()
但是注意细节:(x1可能为负数)
![]()
还要注意:(a,b,c可能为负数,使得 t 为负数)
![]()
到时候还会补充逆元,同余方程等数论知识!!!!