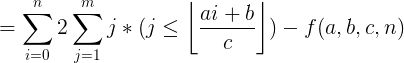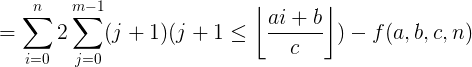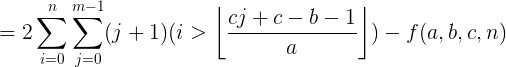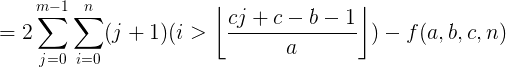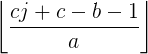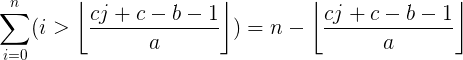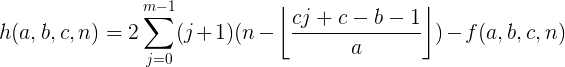【类欧几里得】推导过程
参考博客:类欧几里得算法小结
例题:HDU 6275 Mod, Xor and Everything
题目描述
You are given an integer n.
You are required to calculate (n mod 1) xor (n mod 2) xor ... xor (n mod (n - 1)) xor (n mod n).
The “xor” operation means “exclusive OR”.
输入
The first line contains an integer T (1≤T≤5) representing the number of test cases.
For each test case, there is an integer n (1≤n≤1012) in one line.
输出
For each test case, print the answer in one line.
推导过程主要参考以上博客:
但是有些细节我觉得自己还是不太明白,自己重新写一次博客加深印象!!!!
1、F(a,b,c,n)
1、当 a>=c 或者 b>=c 时:
(此时,a和b都可以分成 整除部分 和 余数部分 表示 ):
2、当 a
在推导之前先给大家一个思想用不等式求和的方式更换一个数:
譬如:
左边: 等差数列求和 , 右边: i 分解成从1~i 个1累加
i=1时: j = 1 满足条件. i = 1 = 1
i=2时: j = 1 , 2 满足条件 i = 1 + 1 = 2
i=3时: j = 1 , 2 , 3 满足条件 i = 1 + 1 + 1 = 3
i=4时: j = 1 , 2 , 3 , 4满足条件 i = 1 + 1 + 1 + 1 = 4
开始推导:
换元法:令 k = j-1 , 因为变量名字可以换回来,所以 j = j - 1
符号两边同时乘以C 不改变 符号方向:同时满足以下式子:
把在乘法过程把下取整符号去掉
把≥变成>
移项作除法得到:
需要用下取整来规范
∵下取整左边变小
∴不改变不等号方向
交换两个求和次序,不改变结果
当i >=[ (cj+c-b-1) / (a) ] +1 为真,
∴起点是:[ (cj+c-b-1) / (a) ] +1 , 终点是:n
共有n - [ (cj+c-b-1) / (a) ] 项,前缀和
形如: 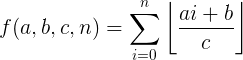 进行类比
进行类比
![]()
2、g(a,b,c,n)
1、当 a>=c 或者 b>=c 时:
2、当 a 分解成不等式累加的形式 换元:k=j-1,最后把 j = k 换回来 省略了一些过程,首先左右乘以c(去掉下取整符号),移项,两边同除以a,添加下取整符号 到了整个化简g的最难的一步了!!! 涉及等差数列求和: 当 i >= [ (cj+c-b-1) / a ] + 1 为真 起点为:i = [ (cj+c-b-1) / a ] + 1 ,终点为:n 当在该区间内时才统计i的求和的值: 所以这个就是等差数列求和 首项为:[ (cj+c-b-1) / a ] + 1 公差为:1 共有 n- [ (cj+c-b-1) / a ] 项 1、当 a>=c 或 b>=c 2、a 在推导之前引入一个等价代换: 此时需要分两部分来讨论:后面显然是f(a,b,c,n),主要是看前半段 注意看这一步,把第二个求和符号的 结束 位置 变成常量 比如: 只看第二个求和符号, i =1 时 , j = 1 i =2 时, j = 1 + 2 i =3 时, j = 1 + 2 + 3 等价于, j ~[1,n] ,当( j <= i )时,这个情况才被考虑. 所以就是: 通过上面的式子进行照葫芦画瓢: 换元法:k=j+1 ,再用 j = k 换回来 省略了一些过程,首先左右乘以c(去掉下取整符号),移项,两边同除以a,添加下取整符号 交换求和次序 前缀和求出: 最后代码是从参考博客那里拿过来的. You are given an integer n. The first line contains an integer T (1≤T≤5) representing the number of test cases. For each test case, print the answer in one line.
![]()
3、h(a,b,c,n)
![]()
![]()
dong likegcd(ll a,ll b,ll c,ll n){
if (!a){
gjx.f=gjx.g=gjx.h=0;
return gjx;
}
if (a>=c||b>=c){
zlt=likegcd(a%c,b%c,c,n);
gjx.f=((ll)(a/c)*n%mo*(n+1)%mo*ni2%mo+(ll)(b/c)*(n+1)%mo)%mo;
(gjx.f+=zlt.f)%=mo;
gjx.g=((ll)(a/c)*n%mo*(n+1)%mo*(2*n+1)%mo*ni6%mo+(ll)(b/c)*(n+1)%mo*n%mo*ni2%mo)%mo;
(gjx.g+=zlt.g)%=mo;
gjx.h=(ll)(a/c)*(a/c)%mo*n%mo*(n+1)%mo*(2*n+1)%mo*ni6%mo;
(gjx.h+=(ll)(b/c)*(b/c)%mo*(n+1)%mo)%=mo;
(gjx.h+=(ll)(a/c)*(b/c)%mo*n%mo*(n+1)%mo)%=mo;
(gjx.h+=(ll)2*(a/c)%mo*zlt.g%mo)%=mo;
(gjx.h+=(ll)2*(b/c)%mo*zlt.f%mo)%=mo;
(gjx.h+=zlt.h)%=mo;
return gjx;
}
ll m=((ll)a*n+(ll)b)/(ll)c;
zlt=likegcd(c,c-b-1,a,m-1);
gjx.f=((ll)n*m%mo-(ll)zlt.f)%mo;
gjx.g=((ll)(n+1)*n%mo*m%mo-(ll)zlt.f-(ll)zlt.h)%mo;
gjx.g=(ll)gjx.g*ni2%mo;
gjx.h=((ll)n*m%mo*(m+1)%mo-(ll)2*zlt.g%mo-(ll)2*zlt.f%mo-(ll)gjx.f)%mo;
return gjx;
}
例题:HDU 6275 Mod, Xor and Everything
题目描述
You are required to calculate (n mod 1) xor (n mod 2) xor ... xor (n mod (n - 1)) xor (n mod n).
The “xor” operation means “exclusive OR”.输入
For each test case, there is an integer n (1≤n≤1012) in one line.输出
#include

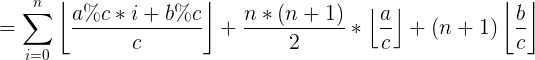
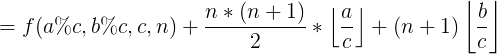
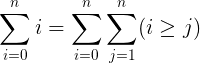
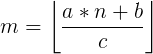
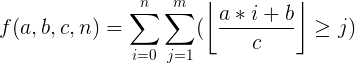
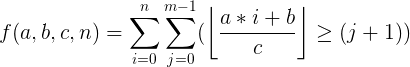

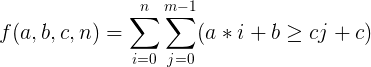
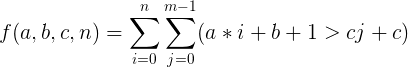

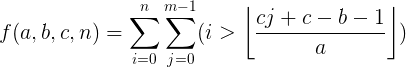
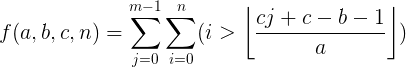
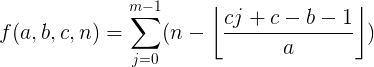

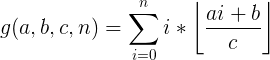

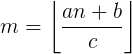

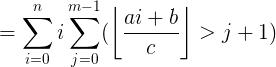

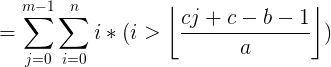
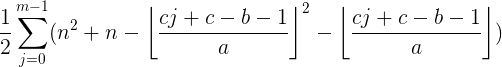
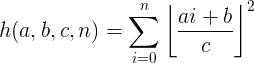
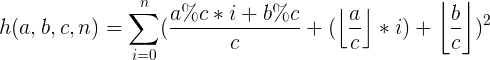


![\large =\sum_{i=0}^{n}[2*\sum_{j=0}^{\frac{ai+b}{c}}j-\frac{ai+b}{c}]](http://img.e-com-net.com/image/info8/d893d44ac7384880a797bcf7369a0a6d.gif)