简单理解卷积码
卷积码(convolutional code)是信道编码的一种。信道编码被用于物理层,目的是减少因不完美信道造成的误码。卷积码的生成方式是将待传输的信息序列通过线性有限状态移位寄存器。接收方使用最大似然法解码(maximum likelihood decoding)。
1. 编码
1.1. 从编码器的角度理解编码过程
卷积码的编码器如图 1 所示,由 K K K 个能存储 k k k 个比特的 stage 和 n n n 个莫二加法运算器以及一个 n n n 位寄存器组成。它的功能是将 k k k 个比特的原始信息比特编成 n n n 比特的信道码。每轮编码只能有 k k k 个比特作为输入, n n n 个比特作为输出。
当编码器运作时执行以下操作:
- stage K K K 先将原先存储的比特丢弃,stage i i i 将存储的比特转移至 stage i + 1 i+1 i+1;
- 向 stage 1 1 1 输入 k 个欲被编码的信息比特;向 stage 1 1 1 输入 k 个欲被编码的信息比特;
- 每个 stage 将其所存储的比特按照预先设定的方式输入至莫二加法器做莫二加法运算,所得结果被存储在 n n n 位寄存器中;每个 stage 将其所存储的比特按照预先设定的方式输入至莫二加法器做莫二加法运算,所得结果被存储在 n n n 位寄存器中;
- 将 n n n 位寄存器的存储作为该轮输入的编码结果输出。将 n n n 位寄存器的存储作为该轮输入的编码结果输出。
- 以上步骤执行至所有信息比特被编码为止。以上步骤执行至所有信息比特被编码为止。
图 1 为 n = 3 n=3 n=3, k = 1 k=1 k=1, K = 3 K=3 K=3 卷积码编码器,这意味着每轮编码只能输入一个比特,有三个比特作为输出。输出序列 C = C 1 C 2 C 3 C=C_1 C_2 C_3 C=C1C2C3 与 stage 之间的关系为: C 1 = S 1 C_1=S_1 C1=S1、 C 2 = S 1 ⨁ S 2 ⨁ S 3 C_2=S_1⨁S_2⨁S_3 C2=S1⨁S2⨁S3、 C 3 = S 1 ⨁ S 3 C_3=S_1⨁S_3 C3=S1⨁S3。
以输入比特“ 1 1 1”作为例子,编码器需要执行以下操作:
- stage 3 3 3 将原先存储的比特“ 0 0 0” 丢弃,stage 2 2 2 将存储的比特“ 0 0 0”转移至 stage 3 3 3,而 stage 1 1 1 将存储的比特“0” 转移至 stage 2 2 2;
- 输入比特“ 1 1 1”最后被存入 stage 1 1 1 中;输入比特“ 1 1 1”最后被存入 stage 1 1 1 中;
- 通过莫二加法运算后输出序列为 C = C 1 C 2 C 3 = 111 C=C_1 C_2 C_3=111 C=C1C2C3=111;通过莫二加法运算后输出序列为 C = C 1 C 2 C 3 = 111 C=C_1 C_2 C_3=111 C=C1C2C3=111;
- 该轮编码结果“ 111 111 111”被输出。该轮编码结果“ 111 111 111”被输出。
1.2. 从 trellis diagram 的角度理解编码过程
一般会将编码的结果在如图 2 所示的 trellis diagram上用箭头表示,这些箭头被称为 branch。trellis diagram 上每一行代表编码的 state,其由 stage 2 2 2 至 stage K K K 内存储的比特排列而成,记为 S = S 2 S 3 … S K S=S_2 S_3…S_K S=S2S3…SK; trellis diagram 上每一列代表被编码比特的第几轮输入。trellis diagram 上每一行与每一列的交汇点被称为 node,代表每轮编码时的 state; branch 上标有一些码字,代表每轮编码的结果,也即上文提到的 n n n 位寄存器的存储内容;所有 branch 组合成一条 path,标识整个编码过程中 state 的变化情况。
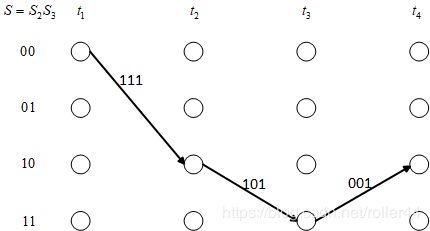
图 2 是以“ 110 110 110”作为图 1 编码器编码输入的 trellis diagram,编码步骤如下:
- 当时刻为 t = t 1 t=t_1 t=t1 时,输入比特“ 1 1 1”,此时移位寄存器的存储为 S 1 S 2 S 3 = 100 S_1 S_2 S_3=100 S1S2S3=100,state 为 S = S 2 S 3 = 00 S=S_2 S_3=00 S=S2S3=00,编码输出为 C = C 1 C 2 C 3 = 111 C=C_1 C_2 C_3=111 C=C1C2C3=111;
- 当时刻为 t = t 2 t=t_2 t=t2 时,再次输入比特“ 1 1 1”,此时移位寄存器的存储为 S 1 S 2 S 3 = 110 S_1 S_2 S_3=110 S1S2S3=110,因此 state 变为 S = S 2 S 3 = 10 S=S_2 S_3=10 S=S2S3=10,而编码输出为 C = C 1 C 2 C 3 = 101 C=C_1 C_2 C_3=101 C=C1C2C3=101;当时刻为 t = t 2 t=t_2 t=t2 时,再次输入比特“ 1 1 1”,此时移位寄存器的存储为 S 1 S 2 S 3 = 110 S_1 S_2 S_3=110 S1S2S3=110,因此 state 变为 S = S 2 S 3 = 10 S=S_2 S_3=10 S=S2S3=10,而编码输出为 C = C 1 C 2 C 3 = 101 C=C_1 C_2 C_3=101 C=C1C2C3=101;
- 当时刻为 t = t 3 t=t_3 t=t3 时,输入比特“ 0 0 0”,此时移位寄存器的存储为 S 1 S 2 S 3 = 011 S_1 S_2 S_3=011 S1S2S3=011,因此 state 变为 S = S 2 S 3 = 11 S=S_2 S_3=11 S=S2S3=11,而编码输出为 C = C 1 C 2 C 3 = 001 C=C_1 C_2 C_3=001 C=C1C2C3=001;当时刻为 t = t 3 t=t_3 t=t3 时,输入比特“ 0 0 0”,此时移位寄存器的存储为 S 1 S 2 S 3 = 011 S_1 S_2 S_3=011 S1S2S3=011,因此 state 变为 S = S 2 S 3 = 11 S=S_2 S_3=11 S=S2S3=11,而编码输出为 C = C 1 C 2 C 3 = 001 C=C_1 C_2 C_3=001 C=C1C2C3=001;
完整信道编码的结果为“ 111101001 111 101 001 111101001”。值得说明的是,在编码前所有的 stage 默认携带比特“ 0 0 0”,所以无论编码器的输入是什么,trellis diagram 上的 path 都从“ 00 00 00” state 开始。
2. 解码
卷积码解码利用最大似然法(maximum likelihood),其包含两个步骤:
- 对于一串接收的序列 R \bf R R,在所有输入方式所能产生的编码序列 C \bf C C 中找到一串与 R 最相似的序列 C ∗ \bf C^{* } C∗ 作为接收原码;
- 根据 C ∗ \bf C^{*} C∗ 在 trellis diagram 中表示的 path 反推出所有输入的原始信息比特。
最大似然法解码在 trellis diagram 上的表现为寻找一条与代表接收序列 R \bf R R 的 path P a t h R Path_{\bf R} PathR 相似度最高的一条 path P a t h C ∗ Path_{\bf C^{* }} PathC∗。
然而遍历所有可能产生的序列伴随着巨大的开销,所以在实际中采用 Viterbi 算法解码 [11]。Viterbi 算法在解码的过程中删减去与接收序列相似度较低的序列,在 trellis diagram 上表现为删除与代表 R \bf R R 的 path P a t h R Path_{\bf R} PathR 中 branch 相似度低的 branch。
卷积码的解码还分为硬解码(hard decision decoding)和软解码(soft decision decoding)两种,前者先将所采样的信号做判别再进行解码,后者直接用被采样信号做解码运算。
下面以硬解码为例结合 trellis diagram 解释 Viterbi 算法。
在硬解码中,判断序列相似度的指标是汉明距离,即要判断 R \bf R R 与 C \bf C C 对应比特不同的位数。在使用 Viterbi 算法进行解码时,需要计算累计错误度量(accumulated error metrics),即每一条可能属于 P a t h C ∗ Path_{\bf C^{* }} PathC∗ 的 branch 所能产生的码字与 P a t h R Path_{\bf R} PathR 对应 branch 的汉明距离之累加。图 1 的 trellis diagram 说明了 Viterbi 算法的执行过程,其假设发送端使用图 1 的接收机如图 2 编码,所发送序列为 C = 111101001 C=111101001 C=111101001;又假设所接收的序列为 R = 110100001 R=110100001 R=110100001。
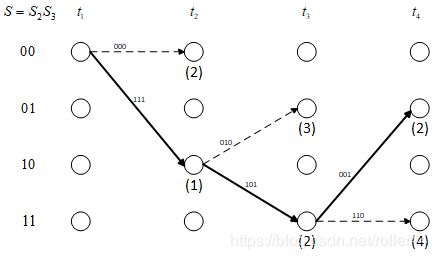
Viterbi 算法具体执行过程如下:
- 卷积码的编码都从“ 00 00 00” state 开始,所以从该 state 开始搜寻属于 P a t h C ∗ Path_{\bf C^{* }} PathC∗ 的 branch。因为 k = 1 k=1 k=1,发送方发送的被编码比特只有“0”或者“1”两种可能,当 t = t 1 t=t_1 t=t1 时,按照图 1 中编码器的编码方式,若发送方编码前输入的比特为“ 0 0 0”,则产生的码字为“ 000 000 000”,其对应 branch 的累计错误度量为 2 2 2;若发送方编码前输入的比特为“ 1 1 1”,则产生的码字为“ 111 111 111”,其对应 branch 的累计错误度量为 1 1 1。说明输入“ 1 1 1”产生的 branch 于 P a t h R Path_{\bf R} PathR 的第一条 branch 最相似,因此被保留,而输入“ 0 0 0”产生的 branch 被删除。
- 而后承接上一步,当 t = t 2 t=t_2 t=t2 时,由于只有到达“ 10 10 10” state 的 branch 被保留,因此解码由“ 10 10 10” state 开始,按照图 1 中编码器的编码方式,若发送方编码前输入的比特为“ 0 0 0”,则产生的码字为“ 010 010 010”,其对应 branch 的累计错误度量为 1 + 2 = 3 1+2=3 1+2=3;若发送方编码前输入的比特为“ 1 1 1”,则产生的码字为“ 101 101 101”,其对应 branch 的累计错误度量为 1 + 1 = 2 1+1=2 1+1=2,少于前者,所以该 branch 被保留、前者被删除。
- 承接上一步,当 t = t 3 t=t_3 t=t3 时,由于只有到达“ 11 11 11” state 的 branch 被保留,因此解码由“11” state 开始,按照图 1 中编码器的编码方式,若发送方编码前输入的比特为“ 0 0 0”,则产生的码字为“ 001 001 001”,其对应 branch 的累计错误度量为 2 + 0 = 2 2+0=2 2+0=2;按照图 1 中编码器的编码方式,若发送方编码前输入的比特为“ 1 1 1”,则产生的码字为“ 110 110 110”,其对应 branch 的累计错误度量为 2 + 2 = 4 2+2=4 2+2=4,多于前者,所以该 branch 被删除、前者被保留。
由此判断 C ∗ = 111101110 C^{*}=111101110 C∗=111101110,而被编码的序列应为“ 110 110 110”。
软解码执行 Viterbi 算法的方式和硬解码执行 Viterbi 算法的方式相似,唯一的区别在于软解码计算累计误差度量 E r r s o f t {\bf Err}_{soft} Errsoft 如下公式而非汉明距离。
E r r s o f t = ∑ i = 1 N ( R i − C i ) 2 {\bf Err}_{soft}=\sum_{i=1}^N (R_i-C_i )^2 Errsoft=i=1∑N(Ri−Ci)2