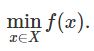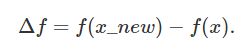爬山算法 ( Hill Climbing )/模拟退火(SA,Simulated Annealing)

一. 爬山算法 ( Hill Climbing )

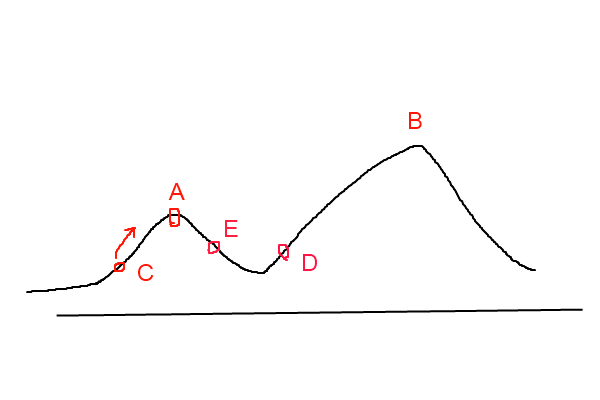
爬山算法是一种简单的贪心搜索算法，该算法每次从当前解的临近解空间中选择一个最优解作为当前解，直到达到一个局部最优解。爬山算法实现很简单，其主要缺点是会陷入局部最优解，而不一定能搜索到全局最优解。假设C点为当前解，爬山算法搜索到A点这个局部最优解就会停止搜索，因为在A点无论向那个方向小幅度移动都不能得到更优的解。

 

二. 模拟退火(SA,Simulated Annealing)思想

在实际日常中，人们会经常遇到如下问题：在某个给定的定义域X内，求函数f(x)对应的最优值。此处以最小值问题举例（最大值问题可以等价转化成最小值问题），形式化为： 

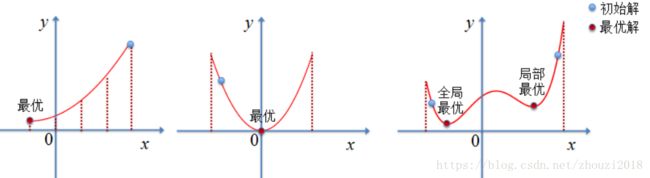
如果X是离散有限取值，那么可以通过穷取法获得问题的最优解；如果X连续，但f(x)是凸的，那可以通过梯度下降等方法获得最优解；如果X连续且f(x)非凸，虽说根据已有的近似求解法能够找到问题解，可解是否是最优的还有待考量，很多时候若初始值选择的不好，非常容易陷入局部最优值。 

随着日常业务场景的复杂化，第三种问题经常遇见。如何有效地避免局部最优的困扰？模拟退火算法应运而生。其实模拟退火也算是启发式算法的一种，具体学习的是冶金学中金属加热-冷却的过程。由S.Kirkpatrick, C.D.Gelatt和M.P.Vecchi在1983年所发明的，V.Čern在1985年也独立发明此演算法。

不过模拟退火算法到底是如何模拟金属退火的原理？主要是将热力学的理论套用到统计学上，将搜寻空间内每一点想像成空气内的分子；分子的能量，就是它本身的动能；而搜寻空间内的每一点，也像空气分子一样带有“能量”，以表示该点对命题的合适程度。演算法先以搜寻空间内一个任意点作起始：每一步先选择一个“邻居”，然后再计算从现有位置到达“邻居”的概率。若概率大于给定的阈值，则跳转到“邻居”；若概率较小，则停留在原位置不动。

一、模拟退火算法基本思想

模拟退火其实也是一种贪心算法，但是它的搜索过程引入了随机因素。在迭代更新可行解时，以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。以下图为例，假定初始解为左边蓝色点A，模拟退火算法会快速搜索到局部最优解B，但在搜索到局部最优解后，不是就此结束，而是会以一定的概率接受到右边的移动。也许经过几次这样的不是局部最优的移动后会到达全局最优点D，于是就跳出了局部最小值。 

根据热力学的原理，在温度为T时，出现能量差为dE的降温的概率为p(dE)，表示为: 

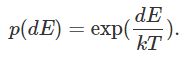
其中k是波尔兹曼常数，值为k=1.3806488(13)×10−23，exp表示自然指数，且dE<0。因此dE/kT<0，所以p(dE)函数的取值范围是(0,1)。满足概率密度函数的定义。其实这条公式更直观意思就是：温度越高，出现一次能量差为p(dE)的降温的概率就越大；温度越低，则出现降温的概率就越小。

在实际问题中，这里的“一定的概率”的计算参考了金属冶炼的退火过程。假定当前可行解为x，迭代更新后的解为x_new，那么对应的“能量差”定义为： 

其对应的“一定概率”为： 

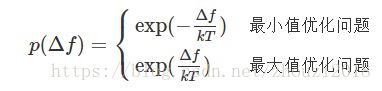
注：在实际问题中，可以设定k=1。因为kT可以等价于一个参数T。如设定k=2、T=1000，等于直接设定T=2000的效果。

二、模拟退火算法描述

1. 初始化：初始温度T（充分大），温度下限Tmin（充分小），初始解状态x(是算法迭代的起点)，每个T值的迭代次数L；
2. 对l=1,2,...,L做第3至第6步；
3. 产生新解x_new: (x_new=x+Δx)；
4. 利计算增量Δf=f(x_new)−f(x)，其中f(x)为优化目标；
5. 若Δf<0(若寻找最大值，Δf>0)则接受x_new作为新的当前解，否则以概率exp(−Δf/(kT))接受x_new作为新的当前解；
6. 如果满足终止条件则输出当前解作为最优解，结束程序。(终止条件通常取为连续若干个新解都没有被接受时终止算法。)；
7. T逐渐减少，且T>Tmin，然后转第2步。

 

 

三、模拟退火算法的优缺点

模拟退火算法的应用很广泛，可以高效地求解NP完全问题，如货郎担问题(Travelling Salesman Problem，简记为TSP)、最大截问题(Max Cut Problem)、0-1背包问题(Zero One Knapsack Problem)、图着色问题(Graph Colouring Problem)等等，但其参数难以控制，不能保证一次就收敛到最优值，一般需要多次尝试才能获得（大部分情况下还是会陷入局部最优值）。观察模拟退火算法的过程，发现其主要存在如下三个参数问题：

　　(1) 温度T的初始值设置问题 
　　温度TT的初始值设置是影响模拟退火算法全局搜索性能的重要因素之一、初始温度高，则搜索到全局最优解的可能性大，但因此要花费大量的计算时间；反之，则可节约计算时间，但全局搜索性能可能受到影响。

　　(2) 退火速度问题，即每个TT值的迭代次数 
　　模拟退火算法的全局搜索性能也与退火速度密切相关。一般来说，同一温度下的“充分”搜索是相当必要的，但这也需要计算时间。循环次数增加必定带来计算开销的增大。

　　(3) 温度管理问题 
　　温度管理问题也是模拟退火算法难以处理的问题之一。实际应用中，由于必须考虑计算复杂度的切实可行性等问题，常采用如下所示的降温方式： 

T=α×T.α∈(0,1).

注：为了保证较大的搜索空间，α一般取接近于1的值，如0.95、0.9。

　　关于爬山算法与模拟退火，有一个有趣的比喻：

　　爬山算法：兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法，它不能保证局部最优值就是全局最优值。

　　模拟退火：兔子喝醉了。它随机地跳了很长时间。这期间，它可能走向高处，也可能踏入平地。但是，它渐渐清醒了并朝最高方向跳去。这就是模拟退火。

附上模拟退火算法伪代码：

四. 使用模拟退火算法解决旅行商问题

　　旅行商问题 ( TSP , Traveling Salesman Problem ) ：有N个城市，要求从其中某个问题出发，唯一遍历所有城市，再回到出发的城市，求最短的路线。

　　旅行商问题属于所谓的NP完全问题，精确的解决TSP只能通过穷举所有的路径组合，其时间复杂度是O(N!) 。

　　使用模拟退火算法可以比较快的求出TSP的一条近似最优路径。（使用遗传算法也是可以的，我将在下一篇文章中介绍）模拟退火解决TSP的思路：

1. 产生一条新的遍历路径P(i+1)，计算路径P(i+1)的长度L( P(i+1) )

2. 若L(P(i+1)) < L(P(i))，则接受P(i+1)为新的路径，否则以模拟退火的那个概率接受P(i+1) ，然后降温

3. 重复步骤1，2直到满足退出条件

　　产生新的遍历路径的方法有很多，下面列举其中3种：

1. 随机选择2个节点，交换路径中的这2个节点的顺序。

2. 随机选择2个节点，将路径中这2个节点间的节点顺序逆转。

3. 随机选择3个节点m，n，k，然后将节点m与n间的节点移位到节点k后面。

五. 算法评价

        模拟退火算法是一种随机算法，并不一定能找到全局的最优解，可以比较快的找到问题的近似最优解。 如果参数设置得当，模拟退火算法搜索效率比穷举法要高。