基于Trie树的多模匹配算法实现和及优化
1.多模匹配算法简介
多模式匹配在这里指的是在"一个字符串"中寻找"多个模式字符字串"的问题。一般来说，给出一个长字串和很多短模式字符串，如何最快最省的求出哪些模式字符串出现在长字串中是我们需要思考的(因为基本上大多数情况下是在给定的长字串中出现我们给的模式字串的其中几个)该算法的应用领域有很多，例如:（1）关键字过滤
（2）入侵检测
（3）病毒检测
（4）分词等
多模匹配算法是一个概念性的称呼，它的具体实现有很多，例如:
（1）Trie树
（2）AC算法
（3）WM算法
2.Trie树实现多模匹配的过程
2.1构造前缀树
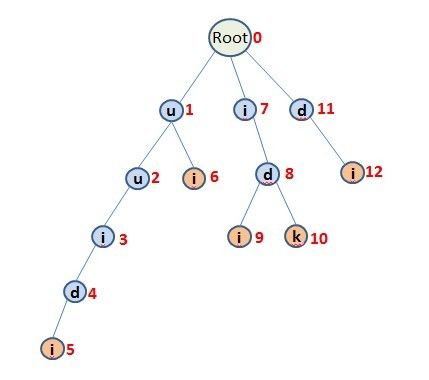
比如我们现在有5个待搜索模式串："uuidi"、"ui"、"idi"、"idk"、"di"，建立如下图所示的前缀树：
（图1）
其中，根节点Root为空，不表示任何字符，其ID为0。依次读取每一个模式串，将模式串的每一个字符添加到树上，并依次顺序编号，编号用
红色数字显示在节点的右边，每一个叶子节点用
黄色背景表示（5,6,9,10,12号节点），表示这里到达一个模式串的结尾（下文称之为尾节点）。如果2个模式串有相同的前缀，则相同的前缀共用相同的节点。例如"uuidi"、"ui"有共同前缀"u"，"idi"、"idk"有共同前缀"id"。
从根节点Root开始，每一个节点的孩子节点表示在此节点可以匹配哪些字符，例如根节点有三个孩子节点1、7、11，则根节点处可以匹配u、i、d三个字符，如果目标字符串相应位置上是这3个字符中的一个，则匹配上某一个孩子节点，接下来的匹配将从该孩子节点继续下去。这是可以匹配上的情况，还有不匹配的情况，对于不匹配的情况我们不是跳回到根节点处重新进行匹配（这样会造成目标字符串的回溯），而是模仿KMP算法中失配时，跳转到FailureNode（失配跳转节点）。例如目标字符串是"uuidk"，我们按照上面构造出的树，会依次经过1、2、3、4节点（匹配上uuid），4的孩子节点5是i，不能匹配上目标串中的k，这个时候我们应该从4跳转到节点8，我们称8是4的FailureNode。
对于每一个树上的节点都应该有对应的FailureNode，以指示在不匹配的情况应该跳转到哪个节点继续进行匹配。
2.2设置每一个节点的FailureNode
其目的和KMP算法很类似，核心的思想是避免不必要的回溯，让搜索始终沿着向前的方向，尽最大可能减小时间复杂度。
上面我们举了一个例子，在节点4失配时，应该跳转到节点8去继续进行匹配，这和KMP算法中在失配时根据失配跳转next数组中记录的位置来进行跳转的原理是一样的，目的是避免对目标串进行回溯匹配。 在KMP算法中求next数组值可以用迭代的方法计算出来，类似的，在多个模式串的情况下，我们计算FailureNode也可以用迭代的方式计算出来。因此FailureNode的作用和KMP中的next数组值是一样的，查找的原则也是一样的，就是 在模式串中查找最长前缀能够匹配上当前失配位置处的最长后缀。
仍以上面图中的节点4来举例，到达节点4的模式串为uuid，对应的后缀为"uid","id","d",我们要找树的前缀中，能匹配上这三个后缀且长度最长的那个位置，首先看"uid",从树的根节点开始（因为要找前缀）没有能匹配上的，在找"id"，找到能匹配上的节点7,8。所以我们设置4的FailureNode为8。如果没有找到能匹配的前缀，则设置FailureNode为根节点Root。
注：可能有看过KMP算法的同学会注意到，我们在找到最长后缀的同时还要看后面的孩子节点是否一样，如果找到的位置后面的孩子节点和本节点的孩子节点一样，那么跳转过去，也必然导致失配。实际上确实如此，但我们仍然简单处理，只看前缀和后缀是否匹配，而不管后面的孩子节点是否一样，其原因我们在后面说明。
针对上图的12个节点，每个节点对应的FailureNode如下表：
（图2）
将每个FailureNode不为0的节点，和其对应的FailureNode节点，用绿色虚线连接起来，形成上图。
每个节点K的FailureNode节点的深度不会超过该节点K的深度，因为从跟节点到FailureNode节点是一个前缀。
另外 每个节点K的FailureNode节点只有一个，不会有多个。因为FailureNode节点的定义是长度最长的前缀匹配失配位置的后缀，长度最长的只可能找到一处，不可能找到两处，如果有两处长度一样，且都是能够匹配的前缀，那么这两个分支按照前缀树的构造方法应该是重合在一起的。
构造完前缀树，设置好每一个节点的FailureNode之后，我们还有一件重要的事情没有做，观察上面的前缀树，当我们来到节点3时，节点2,3组成的字串"ui"其实已经匹配上一个模式串了，但节点3不是一个模式串的尾字符，所以我们无法报告给查询者，我们其实已经匹配上一个模式串了；另外看节点5，当到达节点5时，我们除了匹配上了"uuidi"字串之外，其实我们也匹配上了"idi","di"字符串。为了解决这个问题，我们需要收集每一个节点的模式串匹配情况。
2.3收集每个节点的所有匹配模式串信息
其实要收集每个节点的所有匹配模式串也很简单，观察图2，在节点3位置，应该报告匹配上了模式串"ui"，我们可以看到节点3的FailureNode指向的是节点6。所以获取每个节点的所有匹配模式串的信息可以从该节点的FailureNode入口，如果节点K的FailureNode是一个尾节点，那么到达节点K相当于匹配上了一个模式串。另外，我们再观察节点5，节点5本身就是一个尾节点，所以它有自己的匹配模式串，再看5的FailureNode，指向9,节点9也是尾节点，所以5的匹配模式串除了自身的一个模式串（uuidi）之外还包括9所代表的模式串（idi），而9的FailureNode指向12,12也是一个尾节点，所以节点5也也应该包含节点12的匹配模式串（di）…… 这样进行下去，一直到FailureNode指向了根节点，遍历结束，遍历过程中遇到的所有尾节点都是可匹配的模式串。
在具体的代码实现中，我用一个std::verctor容器来保存一个节点所有的可匹配模式串信息。
另外现在我们可以回答一下上面注一提到的问题。为什么我们没有去检查节点和其FailureNode节点是否有相同的孩子，比如图2中的节点8，我们上面计算出来8的FailureNode是11，但其实因为8有2个孩子9,10，如果8接下来的匹配失配，也就说明目标串中现在出现的字符不是i（9）,k（10），而11的孩子节点12表示（i），则通过FailureNode到达11也必然是会匹配失败的。但是我们仍然设置8的FailureNode为11，是因为如果漏掉过了节点11，我们有可能会漏掉匹配的模式串。例如，5的FailureNode是9，9的FailureNode是12,12的FailureNode是7，如果我们因为5,9，12都没有孩子节点，而直接设置节点5的FailureNode为节点7，那么我们在收集所有的匹配模式串信息时，会漏掉尾节点9,12。
可以考虑一个更极端的情况，比如这样的模式串集："aaaa","aaa","aa","a"，如果我们考虑到节点K的FailureNode的孩子结点不应该全都包含在节点K的孩子节点中(和KMP求NEXT数组前缀和后缀的后一个字符不应该一样同理)，那么我们在目标串"aaaaaaaaaaa"查找模式串集时会漏掉一些匹配的模式串信息报告。
3.1穿线算法
顾名思义，穿线算法就是把符合一定规则的节点用指针连接起来，在进行匹配的时候程序就可以沿着这 条穿好的线进行跳转，不断前进。把各个节点进行穿起来的方法就是设置每个节点的FailNode。
如何设置各个节点的FailNode？这里使用递推的方法来建立。在程序中，一个节点的数据结构中，failjump域用来存放节点的FailNode。可以用如下的方法来建立：
（1）设置Trie树的第一层的不匹配的转移节点
（2）广度遍历Trie树，设置其余层次的不匹配转移节点。在这里设置某节点的failjump域的时候要注意，如果fail.failjump孩子不存在的话，要一直向后迭代直到遇见fail存在孩子或者到达根节点才能停止，否则最后匹配的时候结果不全。伪代码如下：
child= current.child
fail= current;
while(fail!=根节点)
{
fail=fail.failjump;
entry= fail节点的孩子中value等于child.value的节点;
if(entry存在)break;
}
if(entry存在)
child.failjump= entry;
else
child.failjump=根节点;
（3）对算法的说明：假设有三个节点G、P、S，他们的关系为：G -> P -> S。上面的伪代码中，如果current为P节点，那么child就是S节点。这个过程设置了节点P的孩子S的failjump域，该节点（P节点）本身的failjump域是由父节点（G节点）中设置的。因为 这个过程是由树的根部开始的，并且第一层的节点的failjump都被初始化为根节点，因此后续的过程中可以保证出现的每个节点的failjump域都是已经设置过的。因此，按照广度优先遍历树的原则，算法可以不断进行直至树中所有的节点都被设置完毕。
（4）在这个过程中，同时要利用一个vector
3.2 穿线算法的优化
上面的算法中已经把字母相同的节点都穿在了一起，如果匹配过程中发现当前节点（假设当前节点所代表的是a）不存在某个子节点（假设为c），就把failjump指向的节点作为新的当前节点，继续进行查找（按照failjump的定义，该节点也代表a）。若新的当前节点也没有为c的子节点，就一直顺着failjump找下去，直到找到子节点中包含c的a节点或者到达根节点为止。在这个过程中，failjump指向的肯定是离当前节点距离（指的是高度差）最近的且是最大后缀的点点，因此能够保证在寻找过程中首先找到的就是正确的跳转节点。
仔细分析上述过程，还可以做进一步的优化，为什么每次都要按照上面的流程从最近的开始找，一直找到所需要的节点？为什么不直接跳转到目的节点？这个思路固然好，但是当前节点只有一个failjump域，可是当前节点可能有好多个不能匹配的孩子，这些不匹配的孩子未必都会跳向同一个节点。因此需要为每个节点增加一个数据结构，为每个未匹配的孩子都增加一个fail域，发生不匹配的情况时直接读取fail域的信息。这样势必增加存储的开销，但是要获得性能的提升就必须付出代价嘛，因此这点开销是值得的。节点的fail域，实际上是一个长度为26的数组，里面保存了对应的字母要跳转的目标的指针。那么匹配过程是怎样的呢？别着急，听我慢慢道来。
每个节点中其实存在两个数组，一个是son[]数组，一个是fail[]数组，数组长度都是26。其中son[]数组存储的是该节点的孩子节点，若26个字母中对应的孩子存在，则对应的位置存储孩子的指针，否则为空。对于26个字母中不存在的那些孩子，程序肯定要跳转了，那么跳到哪里去呢？3.1中已经给出了如何跳转的描述，这里讲跳转的位置提前计算好，存入fail[]对应的位置就可以了。简单点，可以这么理解，son[]中存放的是当前节点的亲儿子，fail[]存放的是当前节点的干儿子。当亲儿子不存在时，就要找干儿子，这两个肯定儿子会存在一个（当然也只会存在一个）。程序运行时，优先寻找亲儿子，找不到的时候才会寻找干儿子，这样就能保证每次跳转都是有意义的。每跳转一次，要比较的字符串都会向前移动过一个字符。这样，要比较的字符串就不会回溯，提高了效率。
4.算法的时间复杂度分析
多模匹配算法中穷举匹配算法的时间最坏复杂度为O(m*n)，其中n为目标字符串的长度，m为模式串的平均长度。类似Kmp的多模匹配算法的时间复杂度为O(n)。同时通过实验进行了验证，试验结果如下：
Trie树多模匹配时间
| 词典词长 |
建树时间（ms） |
穿线时间（ms） |
穷举匹配 |
KMP匹配 |
加速比 |
||
| 每字符跳转次数 |
匹配用时（ms） |
每字符跳转次数 |
匹配用时（ms） |
||||
| 5～10 |
241 |
461 |
4.75 |
216 |
1 |
130 |
1.66 |
| 15～20 |
670 |
1612 |
5.01 |
551 |
1 |
206 |
2.67 |
| 25～30 |
1068 |
2824 |
5.08 |
923 |
1 |
288 |
3.20 |
| 45～50 |
1863 |
5292 |
5.13 |
1632 |
1 |
443 |
3.68 |
| 65～70 |
2481 |
7477 |
5.15 |
2293 |
1 |
585 |
3.92 |
| 75～80 |
2963 |
9061 |
5.16 |
2771 |
1 |
673 |
4.11 |
其中，词典为随机生成的英语字母序列，规模为10万条。目标字符传为这10万个单词拼接起来的长字符串。从上图中可以可以看出：
（1）穷举法匹配平均每比较一个字符需要跳转5次左右，也就是平均时间复杂度在O(5*n)左右。词典规模越大时该系数越大，但是推测就在5左右，不会大很多。
（2）类似KMP的匹配算法确实做到了每一步跳转都是有效的。但是获得的加速比随着单词长度的增长会逐渐增大。
（3）根据图中的信息可以推测，对随机产生的序列穷举匹配法平均5次就可以后移目标串中的一个字符，理论上的O(m*n)的时间复杂度一般很难遇到。
（4）根据图中的信息可以推测，加速比最高应该在5左右。理论上加速比和穷举匹配中每字符的跳转次数应该非常接近。
5.源代码
如下：
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int MAX = 5000000;
const int Son_Num = 26; //每个孩子的最大分支个数
const int dict_max_len = 30; //词典中单词的最大长度
//---------------------Trie树的定义----------------------------
//节点定义
class Node{
public:
int flag; //节点的是否有单词出现的标记
int count; //单词出现的次数
string word; //到达该节点时出现的单词
vector word_set;//到达该节点时能够匹配上的单词
Node* failjump; //匹配失败时指针的跳转目标
Node* son[Son_Num]; //指向分支节点的指针，这里为26个
Node* fail[Son_Num]; //指向各个分支跳转节点的指针，26个
public:
Node() : flag(0),count(0),word(""){
failjump = NULL;
memset(son, NULL, sizeof(Node*) * Son_Num);
memset(fail, NULL, sizeof(Node*) * Son_Num);
}
};
//trie树的操作定义
class Trie{
private:
Node* pRoot;
private:
void print(Node* pRoot);
public:
Trie();
~Trie();
void insert(string str); //插入字符串
bool search(string str, int &count); //查询字符串
bool remove(string str); //删除字符串
void destory(Node* pRoot); //销毁Trie树
void printAll(); //打印Trie树
void failjump(); //穿线算法
void multi_match_1(string &str, int begin, int end, vector &result); //多模匹配（回溯）
void multi_match_2(string &str, int begin, int end, vector &result); //多模匹配（KMP）
};
//构造函数
Trie::Trie(){
pRoot = new Node();
}
//析构函数
Trie::~Trie(){
destory(pRoot);
}
//打印以root为根的Trie树
void Trie::print(Node* pRoot){
if(pRoot != NULL){
if(pRoot -> word != ""){
cout << pRoot -> count << " " << pRoot -> word << endl;
}
if((pRoot -> word_set).size()){
for(int i = 0; i < (pRoot -> word_set).size(); i++){
cout << "--" << (pRoot -> word_set)[i];
}
cout << endl;
}
for(int i = 0; i < Son_Num; i++){
print(pRoot -> son[i]);
}
}
}
//打印整棵树
void Trie::printAll(){
print(pRoot);
}
//插入新的单词
void Trie::insert(string str){
int index = 0;
Node* pNode = pRoot;
//不断向下搜索单词的字符是否出现
for(int i = 0; i < str.size(); i++){
index = str[i] - 'a';
//字符在规定的范围内时，才进行检查
if(index >= 0 && index < Son_Num){
//父节点是否有指针指向本字符
if(NULL == pNode -> son[index]){
pNode -> son[index] = new Node();
}
//指针向下传递
pNode = pNode -> son[index];
}else{
return;
}
}
//判断单词是否出现过
if(pNode -> flag == 1){
//单词已经出现过，计数器加1
pNode -> count++;
return;
}else{
//单词没有出现过，标记为出现，计数器加1
pNode -> flag = 1;
pNode -> count++;
pNode -> word = str;
}
}
//搜索指定单词，并返回单词出现次数（如果存在）
bool Trie::search(string str, int &count){
Node* pNode = pRoot;
int index = 0;
int i = 0;
while(pNode != NULL && i < str.size()){
index = str[i] - 'a';
if(index >= 0 && index < Son_Num){
//字符在指定的范围内时
pNode = pNode -> son[index];
i++;
}else{
//字符不再指定的范围内
return false;
}
}
//判断字符串是否出现过
if(pNode != NULL && pNode -> flag == 1){
count = pNode -> count;
return true;
}else{
return false;
}
}
//删除指定的单词
bool Trie::remove(string str){
Node* pNode = pRoot;
int i = 0;
int index = 0;
while(pNode != NULL && i < str.size()){
index = str[i] - 'a';
if(index >= 0 && index < Son_Num){
pNode = pNode -> son[index];
i++;
}else{
return false;
}
}
if(pNode != NULL && pNode -> flag == 1){
pNode -> flag = 0;
pNode -> count = 0;
return true;
}else{
return false;
}
}
//销毁Trie树
void Trie::destory(Node* pRoot){
if(NULL == pRoot){
return;
}
for(int i = 0; i < Son_Num; i++){
destory(pRoot -> son[i]);
}
delete pRoot;
pRoot == NULL;
}
//穿线算法
void Trie::failjump(){
queue q;
//将根节点的孩子的failjump域和fail[]域都设置为根节点
for(int i = 0; i < Son_Num; i++){
if(pRoot -> son[i] != NULL){
pRoot -> son[i] -> failjump = pRoot;
q.push(pRoot -> son[i]);
}else{
pRoot -> fail[i] = pRoot;
}
}
//广度遍历树，为其他节点设置failjump域和fail[]域
while(!q.empty()){
Node *cur = q.front();
q.pop();
if(cur -> failjump != NULL){
for(int j = 0; j < Son_Num; j++){
//循环设置跳转域
Node* fail = cur -> failjump;
Node* cur_child = cur -> son[j];
if(cur_child != NULL){
//当孩子存在时，设置孩子的failjump
while(fail != NULL){
if(fail -> son[j] != NULL){
//设置failjump域
cur_child -> failjump = fail -> son[j];
//设置word_set集合
if((fail -> son[j] -> word_set).size()){
cur_child -> word_set = fail -> son[j] -> word_set;
}
if(cur_child -> flag == 1){
(cur_child -> word_set).push_back(cur_child -> word);
}
break;
}else{
fail = fail -> failjump;
}
}
if(cur_child -> failjump == NULL){
cur_child -> failjump = pRoot;
if(cur_child -> flag == 1){
(cur_child -> word_set).push_back(cur_child -> word);
}
}
q.push(cur_child);
}else{
//当孩子不存在时，设置父节点fail[]域
while(fail != NULL){
if(fail -> son[j] != NULL){
//设置对应的fail[j];
cur -> fail[j] = fail -> son[j];
break;
}else{
if(fail == pRoot){
cur -> fail[j] = pRoot;
break;
}else{
fail = fail -> failjump;
}
}
}
}
}
}
}
}
//多模匹配算法1（穷举匹配）
void Trie::multi_match_1(string &str, int begin, int end, vector &result){
int count = 0;
for(int pos = 0; pos < end; pos++){
Node* pNode = pRoot;
int index = 0;
int i = pos;
while(pNode != NULL && i < pos + dict_max_len && i < end){
index = str[i] - 'a';
if(index >= 0 && index < Son_Num){
//字符在指定的范围内时
pNode = pNode -> son[index];
count++;
i++;
//若字符串出现过，输出
if(pNode != NULL && pNode -> flag == 1){
//cout << pNode -> word << endl;
result.push_back(pNode -> word);
}
}
}
}
cout << " 跳转次数：count = " << count << endl;
cout << " 每个字符平均跳转次数：" << double(count)/(end - begin) << endl;
}
//多模匹配算法2（类KMP匹配）
void Trie::multi_match_2(string &str, int begin, int end, vector &result){
int count_1 = 0, count_2 = 0, count_3 = 0;
Node* pNode = pRoot;
int index = 0;
int i = begin;
int word_set_size = 0;
while(pNode != NULL && i < end){
index = str[i] - 'a';
if(index >= 0 && index < Son_Num){
//字符在指定的范围内时
if(pNode -> son[index]){
//该孩子存在，继续向下搜索
pNode = pNode -> son[index];
count_1++;
}else if(pNode != pRoot){
//该孩子不存在，并且当前不是根节点，进行跳转
pNode = pNode -> fail[index];
count_2++;
}else{
//该孩子不存在，并且当前已经是跟节点
count_3++;
}
//若该位置有匹配词语，输出
if(word_set_size = (pNode -> word_set).size()){
for(int i = 0; i < word_set_size; i++){
//cout << (pNode -> word_set)[i] << endl;
result.push_back((pNode -> word_set)[i]);
}
}
//目标串前移
i++;
}
}
cout << " 跳转次数：count_1 = " << count_1 << " count_2 = " << count_2 << " count_3 = " << count_3 << endl;
}
//----------------------辅助代码----------------------------
//生成随机字符串
string rand_string(int min, int max){
char a[MAX+1];
int len = rand()%(max - min) + min;
for(int i = 0; i < len; i++){
a[i] = rand()%26 + 'a';
}
a[len] = '\0';
string str(a);
return str;
}
//-----------------测试代码---------------------------
//获取当前时间（ms）
long getCurrentTime(){
struct timeval tv;
gettimeofday(&tv, NULL);
return tv.tv_sec*1000 + tv.tv_usec/1000;
}
//树的基本操作，增删查改测试
void Test_1(){
//1.建立对象
Trie trie;
string str;
ifstream fin;
fin.open("dict.txt");
//2.建立Trie树
long time_1 = getCurrentTime();
while(getline(fin, str, '\n')){
trie.insert(str);
}
long time_2 = getCurrentTime();
fin.close();
//3.查找单词
str = "siubetamwm";
int count = -1;
long time_3 = getCurrentTime();
bool isFind = trie.search(str, count);
cout << "要查找的字符串：" << str << endl;
long time_4 = getCurrentTime();
if(isFind){
cout << " 该单词存在，存在次数：" << count << endl;
}else{
cout << " 该单词不存在！" << endl;
}
//4.删除单词
str = "lutgjrxjavgfkij";
cout << "要删除的字符串：" << str << endl;
bool isRemove = trie.remove(str);
if(isRemove){
cout << " 该单词存在，删除成功！" << endl;
}else{
cout << " 该单词不存在，删除失败！" << endl;
}
}
//调用词典，多模匹配测试
void Test_2(){
//1.建立对象
Trie trie;
string str;
ifstream fin;
fin.open("dict.txt");
//2.建立Trie树
long time_1 = getCurrentTime();
while(getline(fin, str, '\n')){
trie.insert(str);
}
long time_2 = getCurrentTime();
fin.close();
//3.将短字符串组合为长字符串
string long_str;
ostringstream string_out;
fin.open("dict.txt");
while(getline(fin, str, '\n')){
string_out << str;
}
fin.close();
long_str = string_out.str();
//long_str = rand_string(MAX - 20, MAX);
vector result_1;
vector result_2;
//4.在长字符串中搜索字典中的字符串（方法一：穷举）
cout << "穷举匹配：" << endl;
long time_3 = getCurrentTime();
trie.multi_match_1(long_str, 0, long_str.size(), result_1);
long time_4 = getCurrentTime();
cout << "穷举匹配完毕！" << endl;
//5.进行穿线处理
cout << "穿线处理" << endl;
long time_5 = getCurrentTime();
trie.failjump();
long time_6 = getCurrentTime();
cout << "穿线完毕" << endl;
//6.在长字符串中搜索字典中的字符串（方法二）
cout << "KMP匹配：" << endl;
long time_7 = getCurrentTime();
trie.multi_match_2(long_str, 0, long_str.size(), result_2);
long time_8 = getCurrentTime();
cout << "KMP匹配完毕" << endl;
//7.输出结果
cout << "目标字符串长度：" << long_str.size() << endl;
cout << "穷举匹配结果数量：" << result_1.size() << endl;
cout << "KMP匹配结果数量：" < result_1;
vector result_2;
//4.在长字符串中搜索字典中的字符串（方法一：穷举）
cout << "穷举匹配：" << endl;
long time_5 = getCurrentTime();
trie.multi_match_1(long_str, 0, long_str.size(), result_1);
long time_6 = getCurrentTime();
cout << "穷举匹配完毕！" << endl;
//5.进行穿线处理
cout << "穿线处理" << endl;
trie.failjump();
cout << "穿线完毕" << endl;
//6.在长字符串中搜索字典中的字符串（方法二）
cout << "KMP匹配：" << endl;
long time_7 = getCurrentTime();
trie.multi_match_2(long_str, 0, long_str.size(), result_2);
long time_8 = getCurrentTime();
cout << "KMP匹配完毕" << endl;
//7.输出结果
cout << result_1.size() << endl;
cout << result_2.size() << endl;
sort(result_1.begin(), result_1.end());
sort(result_2.begin(), result_2.end());
cout << "目标字符传长度：" << long_str.size() << endl;
if(result_1 == result_2){
cout << "两种多模匹配方式结果相符：True" << endl;
}else{
cout << "两种多模匹配方式结果不相符：False" << endl;
}
cout << "多模匹配1用时（ms）：" << time_6 - time_5 << endl;
cout << "多模匹配2用时（ms）：" << time_8 - time_7 << endl;
}
int main(){
//Test_1();
Test_2();
//Test_3();
}