多智能体强化学习综述-Lucian Busoniu

Multi-Agent Reinforcement Learning: A Survey
Lucian Busoniu Robert Babuska Bart De Schutter，2006

这篇文章对多智能体强化学习（MARL）的背景，目的，代表性的算法进行了调研。

多智能强化学习算法分类图下图。

1. 背景知识(Backgrounds)

A. 单智能体强化学习

谈多智能体强化学习，首先需要有一般强化学习的概念，一般的强化学习可以参考这里。单智能体情况下，使用马尔可夫决策过程（Markov Decision Process, MDP）来建模:

$$<X,U,f,\rho >$$

其中，$X$是状态空间，$U$是动作空间，$f$是转移概率分布，$\rho$是奖励函数。$k$时刻的长期奖励

$$R_k=\sum _{j=0}^{\infty }{\gamma }^j{r}_{k+j+1}\text{\hspace{1em}(1)}$$

在给定策略$h$下的状态动作函数为$Q^h(x,u)=E\{R_k|x_k=x,u_k=u,h\}$，求解最优策略$h^{\ast }$来最大化$Q$函数。使用Q-learning算法求解：

$$Q_{k+1}(x_k,u_k)=Q_k(x_k,u_k)+\alpha [r_{k+1}+\gamma \underset{u^{\prime }}{\max }{Q}_{k+1}(x_{k+1},u^{\prime })-Q_k(x_k,u_k)]\text{\hspace{1em}(2)}$$

B. 多智能体强化学习

随机博弈（stochastic game, SG）,或称马尔可夫博弈可以定义为

$$<A,X,\{U_i{\}}_{i\in A},f,\{{\rho }_i{\}}_{i\in A}>$$

其中$A=\{1,...,n\}$表示$n$个智能体，$X$是环境状态空间，$\{U_i{\}}_{i\in A}$是动作空间，则联合动作集合$U={\times }_{i\in A}{U}_i$，$f:X\times U\times X\to [0,1]$是状态转移概率分布，${\rho }_i:X\times U\times X\to \mathbb{R},i\in A$是奖励函数。

此时的转移概率、即时奖励、长期回报都依赖联合动作$u_k=[u_{1,k},...,u_{n,k}{]}^{\top }$，$u_k\in U$，$u_{i,k}\in U_i$。此时的策略也是联合策略$h=\{h_i\}$，$h_i:X\times U_i\to [0,1]$。每个智能体的Q函数依赖联合动作和联合策略$Q_i^h=X\times U\to \mathbb{R}$。

如果$X=\varnothing$，SG简化为静态博弈。当${\rho }_1=\cdots ={\rho }_n$，SG是完全合作的；当$n=2,{\rho }_1=-{\rho }_2$，SG是完全竞争的。静态博弈下，纳什均衡（Nash Equilibrum）是对对手的最佳策略。

合作的目的就是确保所有的智能体合理地选择期望联合策略中自己的部分。在多均衡的博弈中，合作归结为均衡的选择，智能体需要不断的选择同一均衡中自己的部分。

2. 多智能体学习目标(Multi-Agent Learning Goal)

完全合作的随机博弈，可以通过最大化联合回报来解决。但是在其他的情况下，确定一个MALRL的目标并不容易，因为智能体的回报函数彼此之间相互关联，难以独立最大化。收敛到均衡点是多智能体学习的基本要求，并且纳什均衡是用的最多的。

聚焦稳定性的文献一般认为智能体之间常常是独立的。而考虑适应能力的话，一般就会考虑其他智能体的行为。如果只考虑稳定性不考虑收敛性，那么就变成对其他智能体的跟踪了。

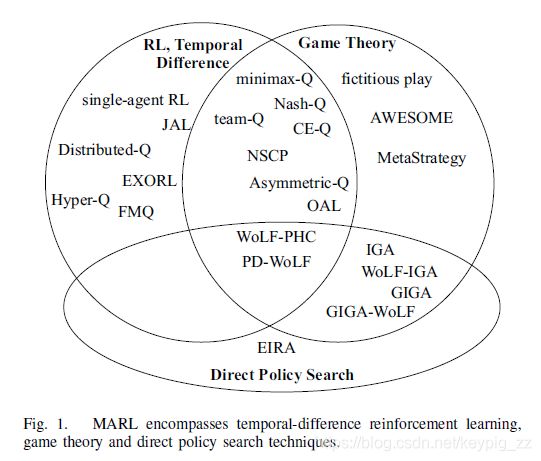
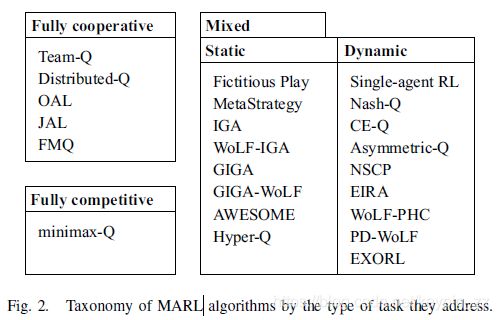
下表对多智能体强化学习算法进行了分类

3. 多智能体强化学习算法简介(Multi-Agent Reinforcement Learning Algorithms)

这里将涉及到的算法按任务进行分类：完全合作、完全竞争、混合任务。

A. 完全合作任务

前面说过，完全合作时${\rho }_1=\cdots ={\rho }_n$，如果存在控制空心，学习目标简化为MDP，动作空间为联合动作空间，此时的Q学习形式为：

$$Q_{k+1}(x_k,{\mathbf{u}}_k)=Q_k(x_k,{\mathbf{u}}_k)+\alpha [r_{k+1}+\gamma \underset{{\mathbf{u}}^{\prime }}{\max }{Q}_{k+1}(x_{k+1},{\mathbf{u}}^{\prime })-Q_k(x_k,{\mathbf{u}}_k)]\text{\hspace{1em}(3)}$$

如果所有的智能体都是独立决策的，并且都采用贪婪策略，协作问题就会出现，即使所有的智能体都使用相同的算法并行学习共同的最优Q函数。理论上他们可以使用贪婪策略最大化共同回报，但是贪婪的动作选择机制以随机的方式打破了协作，最终导致联合动作是次优的。

无需协作模型
Team Q-learning¹假设最优联合动作是唯一的（实际很少发生），因此原来的最优贝尔曼方程可以直接使用。Distributed Q-learning²没有假设协作的条件，但是这种方法只在确定性的场景下有效。每个智能体$i$只通过它自己的动作来维护一个策略$h_i(x)$和一个局部Q函数$Q_i(x,u_i)$，更新方向都是朝着怎加$Q_i$进行的：

$$Q_{i,k+1}(x_k,u_{i.k})=\max \{Q_{i,k}(x_k,u_{i,k}),r_{k+1}+\gamma \max Q_{i,k}(x_{k+1},u_i)\}\text{\hspace{1em}(4)}$$
$$h_{i,k+1}=\{\begin{array}{ll}{u}_{i,k}& \text{if}{\max }_{u_i}{Q}_{i,k+1}(x_{k+1},u_i)̸={\max }_{u_i}{Q}_{i,k}(x_{k+1},u_i)\\ h_{i,k}(x_k)& \text{otherwise}\end{array}\text{\hspace{1em}(5)}$$

在$Q_{i,0}=0$以及共同奖励为正的情况下，可以证明策略会收敛到最佳联合粗略${\mathbf{h}}^{\ast }$
直接协作方法
在随机选择动作的时候有合作或者协商

• Social conventions³和roles⁴会限制智能体的动作选择
• Coordination graph简化协作，如果全局Q函数可以加性的分解为局部Q函数⁵-⁶
• 在协商选择动作的过程中需要通信

非直接协作方法
这类方法使动作选择朝着产出更大的值得方向进行，从而控制智能体走向协作。

• 联合动作学习（Joint Action Learner, JAL）⁷经验地使用从别的智能体行为学习到的模型。
• 频率最大Q值算法主要考虑那些在过去产生好的值的动作出现的频率。
• 最优动态学习（Optimal Adaptive Learning, OAL）⁸，朝着最近被选择的纳什均衡进行。使用其他的方法确保最优纳什均衡最终能够达到。
• JAL和FMQ都是静态博弈。

备注以及一些开放问题
方法的队员之间是相互独立的，而非直接协作方法是队员已知的。直接协作方法在只使用公共知识的情况下队员之间是相互独立的，在有协商的情况下是队员已知的。

为了提高算法的实用能力，我们需要弄清楚算法适用的规模以及在不确定或者部分可观测下的健壮性。免协作方法特备容易受到不确定观测的影响。

交流是MARL中解决协作问题最直接有效的方法，而这部分的研究目前不是很充分。

B. 完全竞争任务

在完全竞争博弈下（两个智能体，${\rho }_1=-{\rho }_2$），使用了最大最小值的概念：假设对手会怎么做会造成我的收益最小，那么把这个最小收益最大化。这种思想催生了像$\text{minimax}-Q$这样的算法:

$$h_{1,k}(x_k,\cdot )=\text{arg}\mathbf{m}1(Q_k,x_k)\text{\hspace{1em}(6)}$$
$$Q_{k+1}(x_k,u_{1,k},u_{2,k})=Q_k(x_k,u_{1,k},u_{2,k})+\alpha [r_{k+1}+\gamma \mathbf{m}1(Q_k,x_{k+1})-Q_k(x_k,u_{1,k},u_{2,k})]\text{\hspace{1em}(7)}$$
其中$\mathbf{m}1$是智能体1的最小最大值：
$$\mathbf{m}1(Q,x)=\underset{h_1(x,\cdot )}{\max }\underset{u_2}{\min }\sum _{u_1}{h}_1(x,u_1)Q(x,u_1,u_2)\text{\hspace{1em}(8)}$$

在上面的算法中Q值没有使用智能体作为下标索引，因为方程隐含的假设了$Q_1=Q=-Q_2$。minmax-Q是真正的与对手无关，因为即使最小最大解有很多方案可以达到，每一种都至少会达到最小最大值这一回报，并且与对手怎么做无关。

如果智能体有一个关于对手的模型（对手已知），实际上可以达到比最小最大值更优的回报。对手模型可以使用$M^{\ast }$这样的算法学习获得⁹。

C. 混合任务

一般情况下，奖励函数不会有什么限制，但是多智能体情况下会产生兴趣冲突，比如竞争资源等。这种情况下，像均衡这样的博弈理论会产生很大的影响。在多均衡的博弈中，智能体需要持续选择同一均衡中自己对应的部分。

接下来先介绍静态重复的博弈，然后介绍动态博弈。

1）重复博弈

• 智能体跟踪方法（Agent-tracking）
• 智能体可知方法（Agent-aware）
• 其他一些问题

2）动态随机博弈

混合动态任务对应于无限制的随机博弈，此时需要考虑所有的MARL问题：延迟奖励、非平稳智能体、冲突目标等。

• 单智能体强化学习（Single-agent RL）应用于MARL存在的问题
  MARL的非平稳特性会导致单智能体RL大部分算法失效，这些算法没有考虑其他智能体的行为影响（智能体只爱），智能体之间智能体之间会产生严重的干扰。尽管有局限性，但是因为比较简单也有不少应用。这些应用中经常将其他智能体的信息编码输入智能体中，相当于间接的是基于别的智能体在做决策。
• 智能体独立方法（Agent-independent）
  这类算法一般都基于Q-learning，并且使用博弈理论求解器求解随机博弈各个阶段的策略和值¹⁰¹¹。在$k$时刻：

$$h_{i,k}(x,\cdot )={\mathbf{s}\mathbf{o}\mathbf{l}\mathbf{v}\mathbf{e}}_i\{Q_{\cdot ,k}(x_k,\cdot )\}\text{\hspace{1em}(9)}$$
$$Q_{i,k+1}(x_k,{\mathbf{u}}_k)=Q_{i,k}(x_k,{\mathbf{u}}_k)+\alpha [r_{i,k+1}+\gamma \cdot {\mathbf{e}\mathbf{v}\mathbf{a}\mathbf{l}}_i\{Q_{\cdot ,k}(x_{k+1},\cdot )\}-Q_{i,k}(x_k,{\mathbf{u}}_k)]\text{\hspace{1em}(10)}$$

其中，${\mathbf{s}\mathbf{o}\mathbf{l}\mathbf{v}\mathbf{e}}_i$返回第$i$个智能体对应部分的均衡（策略），${\mathbf{e}\mathbf{v}\mathbf{a}\mathbf{l}}_i$给出使用此均衡的期望回报。目标设置为在每一个状态收敛到均衡。在更新过程中会用到包含所有智能体的一个Q值表，所有智能体使用相同的算法，所有的动作、奖励都是可观测的。

举例$\mathbf{s}\mathbf{o}\mathbf{l}\mathbf{v}\mathbf{e}$和$\mathbf{e}\mathbf{v}\mathbf{a}\mathbf{l}$，纳什Q学习(Nash Q-learning)：

$$\{\begin{array}{l}{\mathbf{e}\mathbf{v}\mathbf{a}\mathbf{l}}_i\{Q_{\cdot ,k}(x,\cdot )\}=V_i(x,\mathbf{N}\mathbf{E}\{Q_{\cdot ,k}(x,\cdot )\})\\ {\mathbf{s}\mathbf{o}\mathbf{l}\mathbf{v}\mathbf{e}}_i\{Q_{\cdot ,k}(x,\cdot )\}={\mathbf{N}\mathbf{E}}_i\{Q_{\cdot ,k}(x,\cdot )\}\end{array}\text{\hspace{1em}(11)}$$

其中$\mathbf{N}\mathbf{E}$表示计算纳什均衡，${\mathbf{N}\mathbf{E}}_i$表示均衡中智能体的第$i$个策略。$V_i(x,\mathbf{N}\mathbf{E}\{Q_{\cdot ,k}(x,\cdot )\})$表示第$i$个智能体在均衡条件下在状态$x$能获得的反馈期望。Correlated Q-learning¹²以及asymmetric Q-learning工作原理类似，基于相关或者Stackelberg（领航-追随）均衡。在symmetric-Q里面，追随者不需要建立领航者的Q值表，但是领航者必须要知道追随者的动作选择。

• 智能体跟踪方法（Agent-tracking）
  智能体跟踪这类算法会适应学习到的其他智能体的非平稳策略模型而不考虑收敛性。动作必须是可观测的。Non-Stationary Converging Policies（NSCP）算法计算一个模型的最佳反应并用其来估计值函数¹³。
• 智能体可知方法（Agent-aware）
  智能体可知方法一般会考虑收敛的问题。Win-or-Learn-Fast Policy Hill-Climbing (WolF-PHC)算法在WoLF-IGA中将基本的Q学习和梯度策略方法组合¹⁴：

$$h_{i,k+1}(x_k,u_i)=h_{i,k}(x_k,u_i)+\{\begin{array}{ll}{\delta }_{i,k}& \text{if}{u}_i=\arg {\max }_{{\tilde{u}}_i}{Q}_{i,k+1}(x_k,{\tilde{u}}_i)\\ -\frac{{\delta }_{i,k}}{|U_i|-1}& \text{otherwise}\end{array}\text{\hspace{1em}(12)}$$

当智能体要输的时候梯度步长${\delta }_{i,k}$为${\delta }_{\text{l}}$，要赢的时候为${\delta }_{\text{w}}$，${\delta }_{\text{l}}>{\delta }_{\text{w}}$。赢的标准可以是当前策略略和平均策略的比较(WoLF-PHC)或者是策略的二阶差分(PD-WoLF¹⁵)。基本原理就是在要输的时候要尽快逃离目前的形式，而在赢的时候要小心的调整来达到收敛。

Extended Optimal Response (EXORL) 在双智能体任务中，策略朝着最小化另一个智能体奖励的方向更新。

Environment-Independent Reinforcement Acceleration (EIRA) 不对环境做任何假设，这一点来说，这个算法十分通用，但是也使得它无法利用任务的特殊结构。

一些说明
博弈论倾向于在动态情况下使用静态（阶段方式）的解决方案。但是阶段式的解决方案在在混合任务中是否适用现在没有定论。

混合随机博弈中，一般认为智能体是自利的。因此，合作协同技术，像沟通、社会约定、规则等都没有研究。然而在很多混合任务中，智能体是相互合作的，只在某些情况下存在竞争，比如竞争同一个资源。在这样的任务中，合作协同方式是一个可行的选择。

许多混合随机博弈算法都受限于规模和不完整观测，而不完整观测对智能体独立的方法影响较大。

4. 结论与展望（Conclusion and Future Perspectives）

前面回顾了多智能体强化学习面临的挑战，以及针对这些挑战提出的方法，我们对这些方法进行了总结并给出了自己的思考。接下来给出一些更一般的问题。

首先，阶段性地使用博弈论在环境和智能体都是动态变化的场景下不是最合适的。目前为止（本文发表于2006年），基于博弈论的分析仅仅用在动态学习里面。

我们希望学习过程是稳定的，这样智能体的行为更易于控制和分析。我们也希望智能体可以自适应于其他智能体，因为它们的动态特性往往是难以预测的。这样一来，MARL算法不应该仅仅是智能体独立或者仅仅是智能体跟踪。控制论里面的鲁棒理论可以将稳定性和适应性整合为统一的目标。如果一个学习算法可以做到对其他智能体的非平稳特性鲁棒稳定，那么就能在其他智能体行为有限变化的情况下收敛。

从实用的角度出发，现实的学习目标出了通常的非对称要求外，还应该包含暂态表现的边界，如期望达到相应水平的最大时间、暂态表现的下界等。这些方面已经有一些研究了¹⁶。

认为机器学习、博弈论以及控制论的相互结合可以大大促进MARL的发展。

---

1. M. L. Littman, Value-function reinforcement learning in Markov games, Journal of Cognitive Systems Research, vol. 2, pp. 55-66, 2001. ↩︎

2. M. Lauer and M. Riedmiller, An algorithm for distributed reinforcement learning in cooperative multi-agent systems, in Proceedings Seventeenth International Conference on Machine Learning (ICML-00), Stanford University, US, 29 June 2 July 2000, pp. 535-542. ↩︎

3. C. Boutilier, Planning, learning and coordination in multiagent decision processes, in Proceedings Sixth Conference on Theoretical Aspects of Rationality and Knowledge (TARK-96), De Zeeuwse Stromen, The Netherlands, 17-20 March 1996, pp. 195-210. ↩︎

4. M. T. J. Spaan, N. Vlassis, and F. C. A. Groen, High level coordination of agents based on multiagent Markov decision processes with roles, in Workshop on Cooperative Robotics, 2002 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS-02), Lausanne, Switzerland, 1 October 2002, pp. 66-73. ↩︎

5. C. Guestrin, M. G. Lagoudakis, and R. Parr, Coordinated reinforcement learning, in Proceedings Nineteenth International Conference on Machine Learning (ICML-02), Sydney, Australia, 812 July 2002, pp. 227-234. ↩︎

6. J. R. Kok, M. T. J. Spaan, and N. Vlassis, Non-communicative multirobot coordination in dynamic environment, Robotics and Autonomous Systems, vol. 50, no. 2-3, pp. 99-114, 2005. ↩︎

7. C. Claus and C. Boutilier, The dynamics of reinforcement learning in cooperative multiagent systems, in Proceedings 15th National Conference on Articial Intelligence and 10th Conference on Innovative Applications of Articial Intelligence (AAAI/IAAI-98), Madison, US, 26-30 July 1998, pp. 746-752. ↩︎

8. S. Kapetanakis and D. Kudenko, Reinforcement learning of coordination in cooperative multi-agent systems, in Proceedings 18th National Conference on Articial Intelligence and 14th Conference on Innovative Applications of Articial Intelligence (AAAI/IAAI-02), Menlo Park, US,
   28 July 1 August 2002, pp. 326-331. ↩︎

9. D. Carmel and S. Markovitch, Opponent modeling in multi-agent systems, in Adaptation and Learning in Multi-Agent Systems, G. Wei and S. Sen, Eds. Springer Verlag, 1996, pp. 40-52. ↩︎

10. M. Bowling, Multiagent learning in the presence of agents with limitations, Ph.D. dissertation, Computer Science Dept., Carnegie Mellon University, Pittsburgh, US, May 2003. ↩︎

11. A. Greenwald and K. Hall, Correlated-Q learning, in Proceedings Twentieth International Conference on Machine Learning (ICML-03), Washington, US, 21-24 August 2003, pp. 242-249. ↩︎

12. V. K¨on¨onen, Asymmetric multiagent reinforcement learning, in Proceedings IEEE/WIC International Conference on Intelligent Agent Technology (IAT-03), Halifax, Canada, 13-17 October 2003, pp. 336-342. ↩︎

13. M. Weinberg and J. S. Rosenschein, Best-response multiagent learning in non-stationary environments,” in Proceedings 3rd International Joint Conference on Autonomous Agents and Multiagent Systems (AAMAS-04), New York, US, 19-23 August 2004, pp. 506-513. ↩︎

14. M. Bowling and M. Veloso, Multiagent learning using a variable learning rate, Articial Intelligence, vol. 136, no. 2, pp. 215-250, 2002. ↩︎

15. B. Banerjee and J. Peng, Adaptive policy gradient in multiagent learning, in Proceedings 2nd International Joint Conference on Autonomous Agents and Multiagent Systems (AAMAS-03), Melbourne, Australia, 14-18 July 2003, pp. 686-692. ↩︎

16. M. Bowling, Convergence and no-regret in multiagent learning, in Advances in Neural Information Processing Systems 17 (NIPS-04), Vancouver, Canada, 13-18 December 2004, pp. 209-216. ↩︎