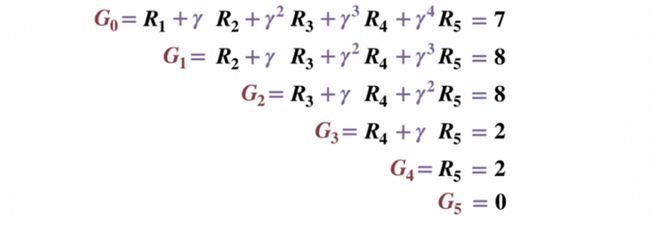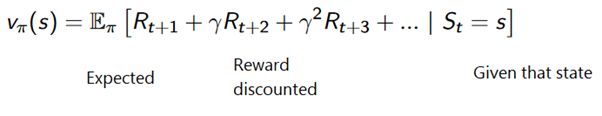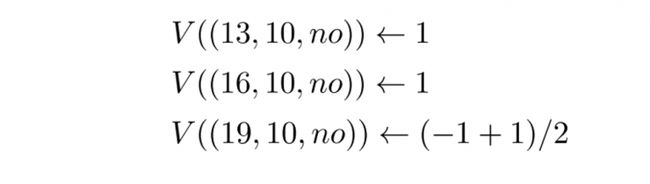强化学习决策涉及因素太多,要知道确切的概率几乎不可能?
强化学习已经席卷了整个 AI 世界。从 AlphaGo 到 AlphaStar,由强化学习提供动力的 AI 智能体已经战胜了越来越多由人类主导的传统活动。通过在某一环境中对智能体行为进行优化以实现最大奖励是强化学习的关键,但是绝大多数强化学习方法需要对环境有完整的了解,而现实中这是难以实现的,基于样本的学习方法(例如蒙特卡洛)则可以解决这一痛点。本文以 21 点游戏为例,对蒙特卡洛方法进行了在强化学习中的应用进行了介绍,雷锋网 AI 科技评论编译如下。
一、引言
强化学习已经席卷了整个 AI 世界。从 AlphaGo 到 AlphaStar,由强化学习提供动力的 AI 智能体已经战胜了越来越多传统上由人类主导的活动。简而言之,这些成就通过在某一环境中对智能体行为进行优化以实现最大奖励而取得。
此前关于 GradientCrescent 的一些文章中,我们对强化学习的各基本方面进行了研究,从基础的强盗系统和基于策略的方法,到在马尔可夫环境中优化基于奖励的行为。所有这些方法都要求我们对环境有全面了解,例如,动态规划要求我们掌握所有可能发生状态转换的完整概率分布。但是,实际上,我们发现大多数系统不可能完全了解完整概率分布,并且由于复杂性、固有的不确定性或计算的局限性,不能显式地表示出概率分布。以气象学家的工作进行类比:预测天气背后涉及的因素非常之多,以至于要知道其中的确切概率几乎是不可能的。
-
GradientCrescent 相关文章阅读可参考:https://medium.com/gradientcrescent
图 1:你能确定飓风形成的准确概率吗?
对于这些情况,基于样本的学习方法(例如蒙特卡洛)是一种解决方案。蒙特卡洛一词通常用于描述任何依赖于随机抽样的估计方法。换句话说,我们并不假设我们了解环境,而是仅通过与环境交互获得的状态、动作和奖励的样本序列从经验中学习。这些方法通过直接观察模型在正常运行时的奖励反馈来判断其状态的平均值。有趣的是,有研究表明,即使不了解环境的动态(可以认为是状态转换的概率分布),我们仍然可以获得最佳行为来最大化奖励。
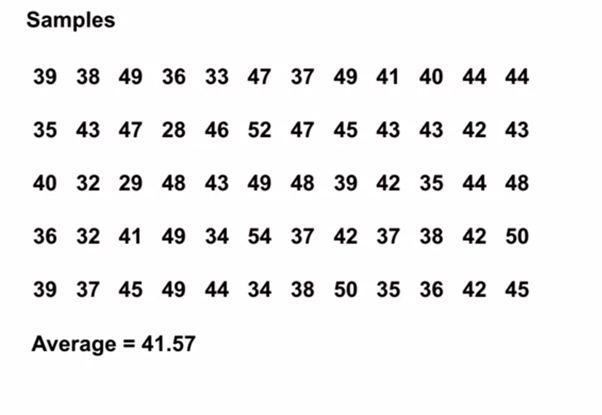
例如,考虑掷 12 个骰子得到的返回值。通过将这些滚动视为单个状态,我们可以对这些返回值进行平均以接近真正的预期返回值。随着样本数量的增加,我们越接近实际的期望返回值。
图 2:掷 12 个骰子 60 次的平均期望值(阿尔伯塔大学)
我忠实的读者可能对这种基于抽样的估计并不陌生,我在此前的相关文章中也对 k-bandit 系统也进行了抽样。蒙特卡洛方法不是比较不同的强盗系统,而是用来比较马尔可夫环境中的不同策略,方法是确定一个状态的值,同时遵循特定的策略直到终止。
二、蒙特卡洛方法的状态值估计
在强化学习中,蒙特卡洛方法是一种通过平均样本回报来估计模型状态值的方法。由于终端状态的需要,蒙特卡洛方法天生适用于偶发环境。由于这个限制,蒙特卡洛方法通常被认为是「离线」的,在这种情况下,所有更新都是在到达终端状态之后进行的。
一个简单的类比是在迷宫中随机导航,它的一种离线的方法是先让智能体到达终点,然后利用经验进行尝试,从而减少在迷宫中花费的时间。相反地,在线方法则是让智能体不断地修正其在迷宫中的行为,比如说当它注意到绿色走廊通向“死胡同”,即便依旧还置身迷宫中也会决定避开它们。我们将在下一篇文章中讨论在线方法。
蒙特卡洛的处理过程可以总结如下:
为了更好地了解蒙特卡洛的工作原理,请参考下面的状态转换图。每个状态转换的奖励都以黑色显示,并且采用 0.5 的贴现因子。让我们暂时搁置实际状态值,并专注于计算本轮的返回值。
图 4:状态转换图。状态编号以红色显示,返回值以黑色显示。
假定终端状态的返回值为 0,那么让我们从终端状态(G5)开始计算每个状态的返回值。请注意,我们已将贴现因子设置为 0.5,从而对最近的状态进行加权。
一般化的公式表示如下:
为了避免将所有返回值都保留在列表中,我们可以逐步地执行蒙特卡洛状态值的更新过程,其方程与传统的梯度下降方程有一些相似之处:
图 5:蒙特卡洛逐步更新过程。S 代表状态,V 代表值,G 代表返回值,而 alpha 代表步长参数。
在强化学习中,蒙特卡洛方法可以进一步分为「首次访问」和「每次访问」。简单地说,两者之间的区别在于蒙特卡洛更新之前,在一轮中可以访问一个状态的次数。「首次访问」蒙特卡洛方法将所有状态的值估计为终止前每个状态首次访问后返回值的平均值,而「每次访问」蒙特卡洛方法将终止前一个状态的 n 次访问后的返回值作为平均值。由于「首次访问」蒙特卡洛方法相对简单,我们将在本文中使用「首次访问」蒙特卡洛。
三、蒙特卡洛方法的策略控制
如果一个模型不能提供策略,那么蒙特卡洛方法也可以用来估计状态动作的值。这比仅使用状态值更有用,因为给定状态中每个动作(q)的值可使得智能体通过对未知环境的观察自动形成策略。
更正式地说,我们可以使用蒙特卡洛方法来估计 q(s, a,pi),从状态 s 开始,采取行动 a,然后遵循策略 pi 时的预期返回值。在蒙特卡洛方法保持不变的情况下,我们针对特定状态额外增加了一个动作维度。如果状态 s 被访问并且动作 A 在其中被执行,则可以认为在该轮中的该状态—动作对(s,a)被访问过。类似地,可以通过「首次访问」或「每次访问」方法来完成状态动作值估计。
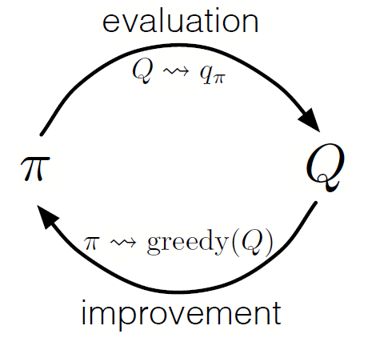
像在动态规划中一样,我们可以使用广义策略迭代(GPI)从状态动作值的观察中形成策略:
通过交替执行策略估计和策略改进步骤,并结合探索起点以确保所有可能的动作都得到访问,我们可以为每个状态实现最佳策略。对于蒙特卡洛 GPI,这种交替通常是在每轮终止后完成的。
四、理解 21 点策略
为了更好地理解蒙特卡洛在评估不同状态值和状态动作值时的实际工作方式,让我们通过 21 点游戏逐步演示。首先,让我们定义游戏的规则和条件:
-
我们只会和庄家对抗,而没有其他玩家参加。这使我们可以将庄家发牌视为环境的一部分。
-
牌面数即为卡牌值。纸牌 J,K 和 Q 的价值均为 10。ace 的值可以为 1 或 11,玩家可以自主选择。
-
双方都有两张卡。玩家的两张牌面朝上,而庄家的一张牌面朝上。
-
目的是使手中的所有卡的总和<= 21。超过 21 则导致爆牌,而双方都为 21 则导致平局。
-
玩家看到自己的牌和庄家的第一张牌后,玩家可以选择要牌或停牌,直到对自己的总和满意为止,之后他将停牌。
-
然后,庄家展示第二张牌——如果两张牌之和少于 17,将继续发牌,直到达到 17,之后停牌。
让我们用 21 点游戏来演示蒙特卡洛。
1、回合 1
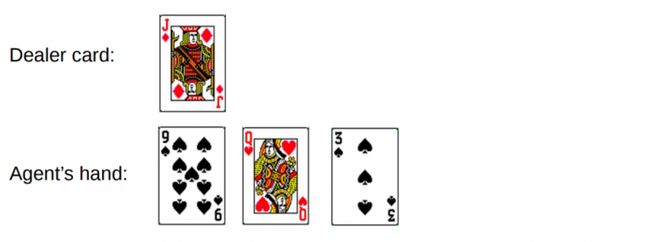
你取得的纸牌之和为 19,你想碰碰运气继续要牌,然后抽出了一张 3,则导致爆牌。爆牌时,庄家只有一张可见的卡,总和为 10。可以显示如下:
图 10:回合 1
当我们爆牌时,此回合的奖励为-1。让我们使用【智能体纸牌之和,庄家纸牌之和,是否获胜?】的格式作为前次状态相应的返回值,该格式如下:
本轮不太走运,让我们进行下一轮。
2、回合 2
你取得的纸牌之和为 19,这次你决定停牌。庄家取得的纸牌之和为 13,然后继续要牌,最终导致爆牌。前次状态描述如下:
图 7:回合 2
让我们描述下这一轮发生的状态和奖励。
随着本轮终止,我们现在可以使用本回合计算出的返回值来更新本轮所有状态值。假设折现系数为 1,我们只需像以前的状态转换一样,将新的奖励加到前面的结果中。由于先前状态 V(19,10,no)的返回值为 -1,因此我们计算出预期返回值并将其分配给我们的状态:
图 8:21 点演示的最终状态值
3、实施
让我们使用「首次访问」的蒙特卡洛方法来实现 21 点游戏,并基于 Sudharsan 等人提出的方法采用 Python 形式对游戏中所有可能的状态值(或不同的操作组合)进行学习 。和往常一样,我们的代码可以在 GradientCrescent Github上获取,链接如下:
-
https://github.com/EXJUSTICE/GradientCrescent
我们将使用 OpenAI Gym 环境来实现这一点。将环境看作是运行游戏的接口,使用最少的代码,从而让我们专注于实现强化学习。方便的是,所有收集到的关于状态、动作和奖励的信息都保存在「观察」变量中,其中这些变量是通过运行游戏积累得到的。
首先让我们导入获取和绘制结果所需的全部开发库。
接下来对我们的 gym 环境进行初始化,并对指导智能体行动的策略进行定义。基本上,我们会持续要牌,直至手中的纸牌之和达到 19 点或更多,然后停牌。
接下来,使用我们的策略为一轮游戏定义生成数据的方法。我们将有关状态、采取的行动以及行动伴随的奖励的信息进行存储。
最后,让我们定义「首次访问」的蒙特卡洛预测函数。首先,我们初始化一个空字典来存储当前状态值,以及另一个字典来存储所有轮游戏中每个状态的条目数。
对于每一轮游戏,我们都调用先前的「 generate_episode 」方法来生成有关状态值和该状态后获得的奖励的信息。我们还初始化了一个变量来存储增量返回值。接下来,我们获得该轮中访问的每个状态的奖励和当前状态值,并使用该步骤的奖励来增加我们的返回值变量。
回想一下,当我们执行「首次访问」的蒙特卡洛时,我们只访问单轮游戏中的单个状态。因此,我们对状态字典执行条件检查,以查看状态是否已被访问。如果满足此条件,则可以使用先前定义的蒙特卡洛状态值更新过程来计算新值,并将对该状态的观察次数增加 1。然后,对下一轮游戏重复此过程,从而最终获得平均返回值。
让我们执行程序看看我们的结果吧!
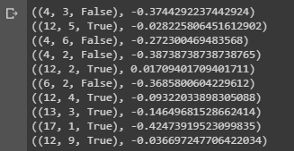
图 15:输出样本显示了多次 21 点游戏的状态值
输出样本显示了多次 21 点游戏的状态值。
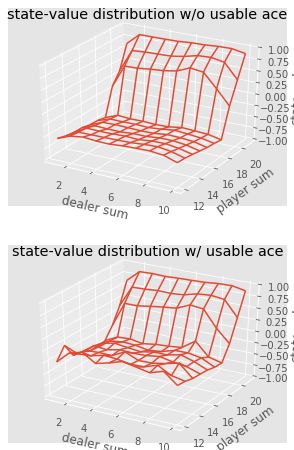
我们可以继续观察 5000 轮游戏的蒙特卡洛,并绘制状态值分布来描述玩家和庄家的任何组合的值。
图 16:不同 21 点游戏组合的状态值可视化
现在让我们总结一下我们学到的知识。
-
基于样本的学习方法使我们可以简单地通过采样来估计状态和状态动作值,而无需任何迁移动态知识。
-
蒙特卡洛方法依赖于模型的随机抽样,观察模型返回的奖励,在正常操作期间收集信息来定义其状态的平均值。
-
通过蒙特卡洛方法进行广义策略迭代是可行的。
-
21 点游戏中玩家和发牌手所有可能组合的值可以通过重复的蒙特卡洛模拟来判断,从而为优化策略开辟了道路。
对蒙特卡洛方法的介绍到此结束。在下一篇文章中,我将介绍以时序差分学习的形式继续进行基于样本的在线学习方法。
参考文献
-
Sutton et. al, Reinforcement Learning(书籍链接:https://books.google.com/books?id=PwnrBwAAQBAJ&printsec=frontcover&dq=Reinforcement+Learning&hl=zh-CN&sa=X&ved=0ahUKEwjB25vcgP3lAhUUa94KHcPODyMQ6AEIKDAA#v=onepage&q=Reinforcement%20Learning&f=false)
-
White et. al, Fundamentals of Reinforcement Learning, University of Alberta
-
Silva et. al, Reinforcement Learning, UCL
-
Platt et. Al, Northeaster University(论文链接:http://www.ccs.neu.edu/home/rplatt/cs7180_fall2018/slides/monte_carlo.pdf)
via https://towardsdatascience.com/optimizing-blackjack-strategy-through-monte-carlo-methods-cbb606e52d1b