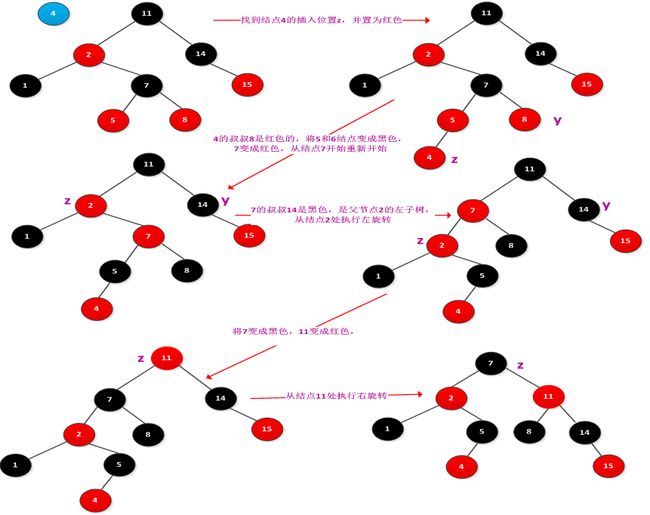
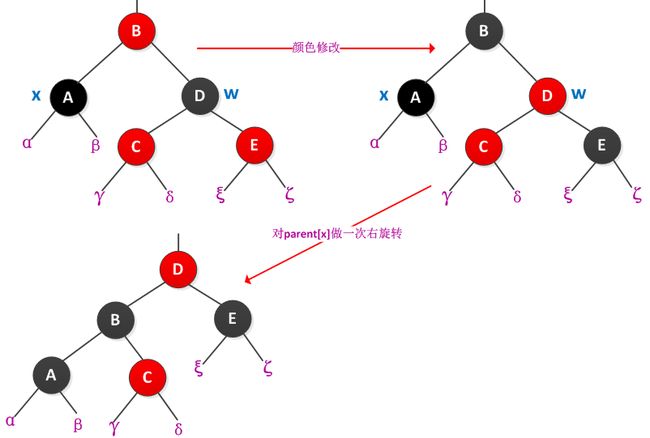
MIT:算法导论——10.平衡搜索树-红黑树
【红黑树】是一棵二叉搜索树,它在每个结点上增加了一个存储位来表示结点的【颜色】,
可以是RED或BLACK。红黑树保证没有一条路径会比其他路径长出2倍,因而是近似【平衡】的。
【树中结点的5个属性】color、key、left、right和p。
一棵红黑树满是足下面【红黑性质】的二叉搜索树:
(1)每个结点是红色或是黑色。
(2)根结点和每个叶节点(NIL)是黑色的。
(3)每个红色结点有黑色父节点。
或者说每个红色结点,它的两个子结点都是黑色的。
(4)每个结点x到页结点的简单路径中,黑色结点数相等。
【补充】可以用哨兵结点T.nil来代表NIL。
【旋转】// x为旋转的根结点
LEFT-ROTATE( T, x )
y = x.right // set y
// 挂载y的左子树为x右子树
x.right = y.left // turn y's left subtree into x's right subtree
if y.left != T.nil
y.left.p = x // 挂载子结点时,是双向的指针
// 连接x.p与y
if x.p == T.nil// link x's parent to y
T.root = y
else if x == x.p.left
x.p.left = y
else
x.p.right = y
y.p = x.p
//将x与y连接
y.left = x // put x on y's left
x.p = y【插入】// z为待插入结点
RB-INSERT( T, z )
x = T.root
y = T.nil
while x != T.nil
y = x
if z.key < x.key
x = x.left
else
x = x.right
// 找到位置后,实际插入
// 2014-6-15 11:06:45 一开始没考虑到y为空时
z.p = y
if y == T.nil
T.root = z
else if z.key < y.key
y.left = z
else
y.right = z
z.left = T.nil
z.right = T.nil
z.color = RED
RB-INSERT-FIXUP( T, z )【保持红黑性质】// z为不满足红黑性质的底层结点
RB-INSERT-FIXUP( T, z )
while z.p.color == RED // 可以改为:z != root and z.p.color == RED
if z.p = z.p.p.left // 整个不平衡位于z.p.p的左子树
y = z.p.p.right
if y.color == RED
z.p.color = BLACK
y.color = BLACK
z.p.p.color = RED
z = z.p.p
else if z = z.p.right
z = z.p
LEFT-ROTATE( T, z )
z.p.color = BLACK
z.p.p.color = RED
RIGHT-ROTATE( T, z.p.p )// 此时再用z = z.p.p 也可以,不过没必要
else( same as then clause
with "right" and "left" exchanged )
T.root.color = BLACK // 如果y.color == RED且y.p.p为T.root,对根着色后可以直接结束了。
// T.root.color位于while之外【删除结点z】
要删除结点z,先按照二叉搜索树的方式进行删除,再修复树的红黑性质。
先赋值y = z。
(1)若z左子树与右子树都不空,则将z与y的key值进行对换,这样实际变成删除y。经(1)预处理后再执行(2)
(2)赋值x = y->right或者 x = y->left,然后将x移植到所在的位置,记录y的颜色然后删除y。
(3)如果y的颜色为黑色,删除后破坏了红黑性质,再执行红黑性质的修复工作。
=====================================================================================
我的代码:
#ifndef ALGORITHM_RBTREE_H_
#define ALGORITHM_RBTREE_H_
#include
using namespace std;
#define RED 0
#define BLACK 1
// enum 怎么用呢
template
class RBTree;
template
class RBTreeNode{
friend RBTree;
public:
RBTreeNode( int c ) : color( c ){}
RBTreeNode( const T& k, int c ) : key(k), color( c ){}
RBTreeNode( int c, RBTreeNode *l, RBTreeNode *r, RBTreeNode *p ) :
key( k ), color( c ), left( l ), right( r ), parent(p){}
~RBTreeNode(){}
private:
T key;
int color;
RBTreeNode *left, *right, *p;
};
#define STATIC
template
class RBTree{
friend ostream& operator<< ( ostream& out, RBTree& rbt);
public:
RBTree(){ nil = new RBTreeNode( BLACK ); root = nil; }
ostream& InOrder( RBTreeNode* t, ostream& out )
{ return InOrder( Visit, t, out ); }// &RBTree::Visit
void PostOrder( void ( *Visit )( RBTreeNode* t ), RBTreeNode* t );
~RBTree()
{ PostOrder( freeNode, root ); }
void LeftRotate( RBTreeNode* x );
void RightRotate( RBTreeNode *x );
void RBInsert( RBTreeNode* z );
void RBInsertFixup( RBTreeNode* z );
RBTreeNode* TreeMinimum( RBTreeNode* z );
void RBTransplant( RBTreeNode* u, RBTreeNode* v );// 用v替代u,但v与u所指不变
void RBDelete( RBTreeNode* z );
void RBDeleteFixup( RBTreeNode* x );
RBTreeNode* GetParent( RBTreeNode* z )
{ return z->p; }
bool IsRoot( RBTreeNode* z )
{ return z == root; }
private:
#ifdef STATIC
static T& Visit( RBTreeNode* t );
static void freeNode( RBTreeNode* t );
#endif
ostream& InOrder( T& ( *Visit )( RBTreeNode *t ), RBTreeNode *t, ostream& out );
RBTreeNode *root;
RBTreeNode *nil;
};
#ifdef STATIC
template
T& RBTree::Visit( RBTreeNode* t )
{
return t->key;
}
#endif
template
ostream& RBTree::InOrder( T& ( *Visit )( RBTreeNode *t ), RBTreeNode *t, ostream& out )
{
//while( t != nil ){// 2014-6-16 17:02:17
if( t != nil ){
InOrder( Visit, t->left, out );
out << Visit( t );
#if 1
if( t->color == BLACK )
out << ",BLACK";
else
out << ",RED";
if( t->left != nil )
out << ",left=" << t->left->key;
if( t->right != nil )
out << ",right=" << t->right->key;
out << "\n";
#else
out << " ";
#endif
InOrder( Visit, t->right, out );
}
return out;
}
template
ostream& operator<<( ostream& out, RBTree& rbt)
{
rbt.InOrder( rbt.root, out );
return out;
}
template
void RBTree::freeNode( RBTreeNode* t )
{// 当我们在外部定义static成员时,无须重复指定static保留字;
// 该保留字只出现在类定义体内部的声明处。
//if( t != nil )
// if( t == t->p->left )
// t->p->left = nil;
// else
// t->p->right = nil;
delete t;
}
template
void RBTree::PostOrder( void ( *Visit )( RBTreeNode* t ), RBTreeNode* t )
{
if( t != nil ){
PostOrder( Visit, t->left );
PostOrder( Visit, t->right );
Visit( t );
}
}
template
void RBTree::LeftRotate( RBTreeNode *x )
{
RBTreeNode *y = x->right;
// 挂载y的左子树为x右子树
x->right = y->left;// 一定要改变
if( y->left != nil )
y->left->p = x;
// link x's parent to y
if( x->p == nil )
root = y;
else if( x == x->p->left )
x->p->left = y;
else
x->p->right = y;
y->p = x->p;
// put x on y's left
y->left = x;
x->p = y;
}
template
void RBTree::RightRotate( RBTreeNode *x )
{
RBTreeNode *y = x->left;
// 挂载y的左子树为x右子树
x->left = y->right;
if( y->right != nil )
y->right->p = x;
// 将x.p与y相连接
if( x->p == nil )
root = y;
else if( x == x->p->left )
x->p->left = y;
else
x->p->right = y;
y->p = x->p;
// 将x连接为y的右子树
y->right = x;
x->p = y;
}
template
void RBTree::RBInsert( RBTreeNode *z )
{
RBTreeNode *x = root, *y = nil;
while( x != nil ){
y = x;
if( z->key < x->key )
x = x->left;
else
x = x->right;
}
// 找到位置后,实际插入
// 2014-6-15 11:06:45 一开始没考虑到y为空时
if( y == nil )
root = z;
else if( z->key < y->key )
y->left = z;
else
y->right = z;
z->p = y;
// 初始化z的属性
z->left = nil;
z->right = nil;
// z->color = RED;// 在构造函数里实现
this->RBInsertFixup( z );
}
template
void RBTree::RBInsertFixup( RBTreeNode *z )
{
RBTreeNode *y = nil;
while( z->p->color == RED ){
if( z->p == z->p->p->left ){
y = z->p->p->right;
if( y->color == RED ){ // 情况1
z->p->p->color = RED;
z->p->color = BLACK;
y->color = BLACK;
z = z->p->p;
}else{
if( z == z->p->right ){ // 情况2
z = z->p;
LeftRotate( z );
}
z->p->p->color = RED; // 情况3
z->p->color = BLACK;
RightRotate( z->p->p );
}
}else{
y = z->p->p->left;
if( y->color == RED ){ // 情况2-1
z->p->p->color = RED;
z->p->color = BLACK;
y->color = BLACK;
z = z->p->p;
}else{
if( z == z->p->left ){ // 情况2-2
z = z->p;
RightRotate( z );
}
z->p->p->color = RED; // 情况2-3
z->p->color = BLACK;
LeftRotate( z->p->p );
}
}
}
root->color = BLACK;
}
template
void RBTree::RBTransplant( RBTreeNode* u, RBTreeNode* v )// 用v替代u,但v与u所指不变
{// 只是修改u与父节点的连接,为v与u.p的连接。
if( u->p == nil )
root = v;
else if( u == u->p->left )
u->p->left = v;
else
u->p->right = v;
v->p = u->p;
}
template
void RBTree::RBDelete( RBTreeNode* z )
{
RBTreeNode *y = z, *x = nil;
int y_original_color = y->color;
if( z->left == nil ){
x = z->right;// 一开始丢了:2014-6-17 16:01:49
RBTransplant( z, z->right );
}else if( z->right == nil ){
x = z->left;// 一开始丢了:2014-6-17 16:01:49
RBTransplant( z, z->left );
}else{
y = TreeMinimum( z->right );// 待实现:2014-6-17 9:27:01
y_original_color = y->color;
x = y->right; // y为右子树最小值,故y->left == nil。
if( y->p == z )
x->p = y;
else{
RBTransplant( y, y->right );
y->right = z->right;
z->right->p = y;
}
RBTransplant( z, y );
y->left = z->left;
z->left->p = y;
y->color = z->color;
}
if( y_original_color == BLACK )
RBDeleteFixup( x );
}
template
void RBTree::RBDeleteFixup( RBTreeNode* x )
{
RBTreeNode *w = nil;
while( x != root && x->color == BLACK ){
if( x == x->p->left ){
w = x->p->right;
// 情况1:x的兄弟w为红色,则w的儿子必然全黑,w父亲p也为黑。
if( w->color == RED ){
w->color = BLACK; // 交换x->p与x->p->right颜色,左旋x.p
x->p->color = RED;
LeftRotate( x->p );
w = x->p->right;
}
// 经过情况1处理,x的右兄弟结点w变为黑色。即为情况2、3、4的前提条件
// x.p的颜色可以为红色,也可以为黑色。
// 情况2:x的兄弟w为黑色,且w的两个孩子都是黑色
if( w->left->color == BLACK && w->right->color == BLACK ){
w->color = RED;// 实质为都上移一层黑色,留下什么算什么;
x = x->p;// x->p红色就结束,黑色则新一轮循环;不过,最后将x->p设为黑色。
}else{
// 情况3:x的兄弟w为黑色,且w的右孩子为黑色,左孩子为红色。
if( w->right->color == BLACK ){// 两者中至多有一个黑,所以w->left为红色。
w->left->color = BLACK;
w->color = RED;
RightRotate( w );// 将w的红色左孩子,放到w的右孩子位置
w = x->p->right;
}
// 经过3,w的右孩子变为红色。
// 情况4:x的兄弟w为黑色,且w的右孩子为红色。
// 将w的黑色,转移到w的右孩子;同时,将w插入到x.p的左孩子位置。
w->right->color = BLACK;
w->color = x->p->color;
x->p->color = BLACK;
LeftRotate( x->p );
x = root;
}
}else{
w = x->p->left;
// 情况1:x的兄弟w为红色,则w的儿子必然全黑,w父亲p也为黑。
if( w->color == RED ){
w->color = BLACK; // 交换x->p与x->p->left颜色,左旋x.p
x->p->color = RED;
RightRotate( x->p );
w = x->p->left;
}
// 经过情况1处理,x的右兄弟结点w变为黑色。即为情况2、3、4的前提条件
// x.p的颜色可以为红色,也可以为黑色。
// 情况2:x的兄弟w为黑色,且w的两个孩子都是黑色
if( w->left->color == BLACK && w->left->color == BLACK ){
w->color = RED;// 实质为都上移一层黑色,留下什么算什么;
x = x->p;// x->p红色就结束,黑色则新一轮循环;不过,最后将x->p设为黑色。
}else{
// 情况3:x的兄弟w为黑色,且w的右孩子为黑色,左孩子为红色。
if( w->left->color == BLACK ){// 两者中至多有一个黑,所以w->left为红色。
w->left->color = BLACK;
w->color = RED;
LeftRotate( w );// 将w的红色左孩子,放到w的右孩子位置
w = x->p->left;
}
// 经过3,w的右孩子变为红色。
// 情况4:x的兄弟w为黑色,且w的右孩子为红色。
// 将w的黑色,转移到w的右孩子;同时,将w插入到x.p的左孩子位置。
w->left->color = BLACK;
w->color = x->p->color;
x->p->color = BLACK;
RightRotate( x->p );
x = root;
}
}
}
x->color = BLACK;
}
template
RBTreeNode* RBTree::TreeMinimum( RBTreeNode* z )
{
while( z->left != nil )
z = z->left;
return z;
}
#endif // ALGORITHM_RBTREE_H_ 测试代码——
#include "10_RedBlackTree.h"
#include
#include
using namespace std;
int main( void )
{
cout << "2014-6-17 16:12:25" << endl;
freopen( "out.txt", "w+", stdout );
RBTree rbt;
//cout << rbt << endl;
int i;
RBTreeNode *y[10], *z;
// for( i = 9; i >= 0; --i ){
for( i = 0; i < 10; ++i ){
RBTreeNode *x = new RBTreeNode( i * 2, RED );
rbt.RBInsert( x );\
y[i] = x;
//cout << rbt << "******" << endl;
}
cout << rbt << endl;
z = y[0];
//while( !rbt.IsRoot( z ) ){
for( i = 4; i < 10; ++i ){
rbt.RBDelete( y[i] );
cout << rbt << endl;
//z = rbt.GetParent( z );
}
return 0;
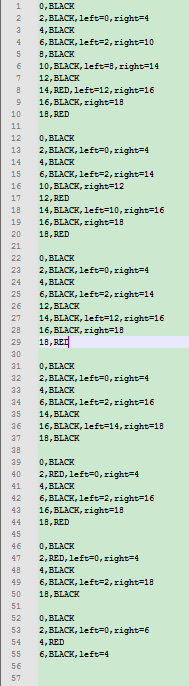
} 测试结果——
O(∩_∩)O哈哈哈~ 终于大功告成~\(≧▽≦)/~啦啦啦 2014-6-17 16:17:27
删除方法的简化代码——
template
void RBTree::RBDelete_Test( RBTreeNode* z )
{
RBTreeNode *y = z, *x = nil;
int y_original_color;
if( z->left != nil && z->right != nil ){
y = TreeMinimum( z->right );
z->key = y->key;
}
y_original_color = y->color;
if( y->left == nil ){
x = y->right;
RBTransplant( y, y->right );
}else{
x = y->left;
RBTransplant( y, y->right );
}
freeNode( y );// 防止内存泄露:2014-6-17 16:30:30
if( y_original_color == BLACK )
RBDeleteFixup( x );
} 理论补充:
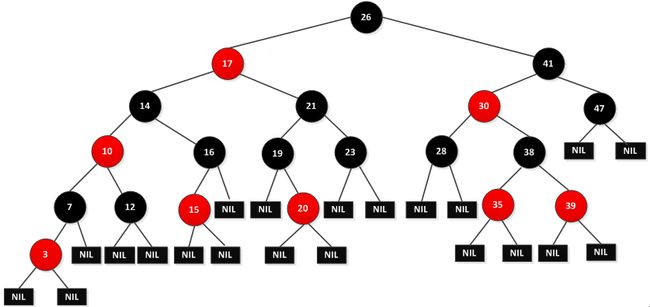
1.如下图是一棵红黑树:
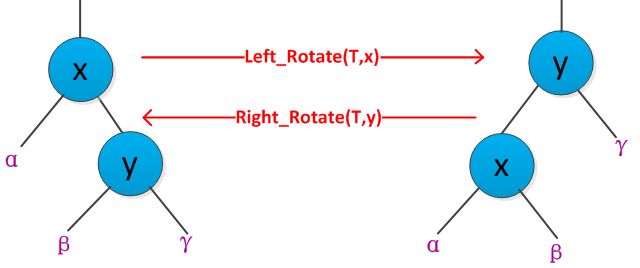
2.旋转
在红黑树上进行结点插入和删除操作时,会改变树的结构形状,导致结果可能不满足了红黑树的某些性质,为了保证每次插入和删除操作后,仍然能报维持红黑树的性质,需要改变树中某些结点的颜色和指针结构。其中的指针结构的改变通过旋转完成的。书中给出了两种旋转:左旋转和右旋转。如下图是旋转过程:
为了更好的理解旋转操作,书中给出了一个左旋转的例如,如下图所示: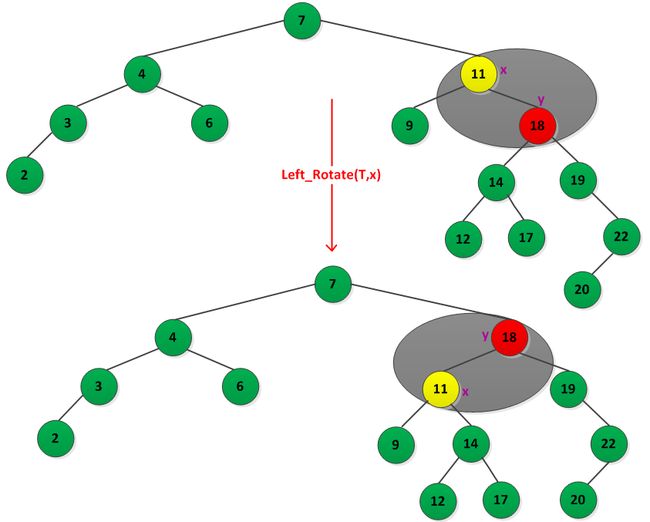
3.插入
情况1):z的叔叔结点y是红色的
此时parent[z]和y都是红色的,解决办法是将z的父节点parent[z]和叔叔结点y都着为黑色,而将z的祖父结点parent[parent[z]]着为红色,然后从祖父结点parent[parent[z]]继续向上判断是否破坏红黑树的性质。处理过程如下图所示: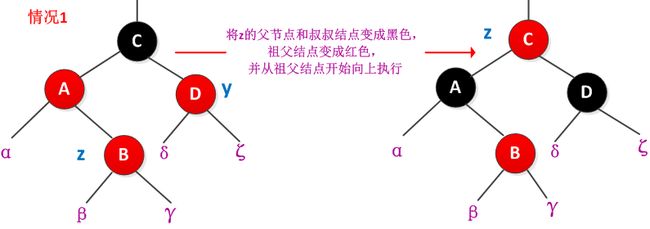
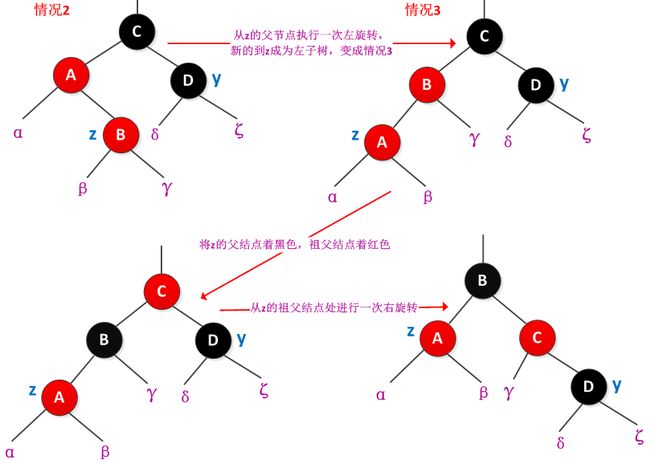
情况2):z的叔叔y是黑色的,而且z是右孩子
情况3):z的叔叔y是黑色的,而且z是左孩子
情况2和情况3中y都是黑色的,通过z是左孩子还是右孩子进行区分的。可以将情况2通过旋转为情况3。情况2中z是右孩子,旋转后成为情况3,使得z变为左孩子,可以在parent[z]结点出使用一次左旋转来完成。无论是间接还是直接的通过情况2进入到情况3,z的叔叔y总是黑色的。在情况3中,将parent[z]着为黑色,parent[parent[z]]着为红色,然后从parent[parent[z]]处进行一次右旋转。情况2、3修正了对性质4的违反,修正过程不会导致其他的红黑性质被破坏。修正过程如下图所示:
4.删除
在循环过程中,x总是指向具有双重黑色的那个非根结点。设w是x的兄弟结点,因为x是双重黑色的,故w不可能是NIL。书中分四种情况讨论:
情况1:x的兄弟w是红色的
此时因为x是双重黑色,贡献两个黑色结点,所有w必有黑色孩子。此时将w着为黑色,parent[x]为红色,在对parent[x]做一次左旋转。此时x的新兄弟w是黑色,这样将情况1转换为情况2、3或4。情况1的处理过程下图所示: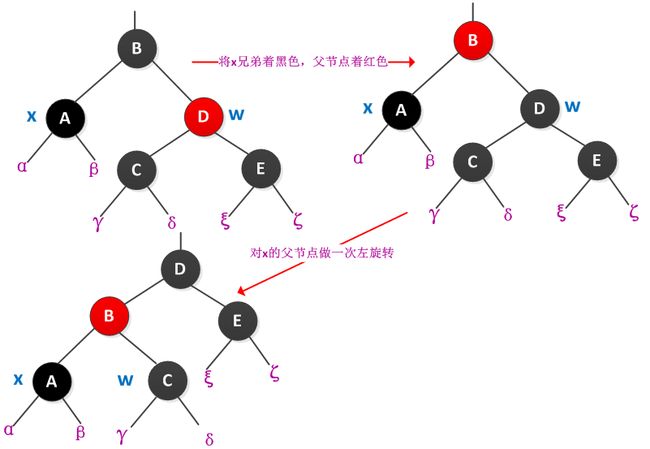
情况2:x的兄弟w是黑色的,而且w的两个孩子都是黑色的。
处理过程是从x和w上去掉一重黑色,即x只有一重黑色而w着为红色,给x的父节点parent[x]添加额外黑色。处理过程如下图所示: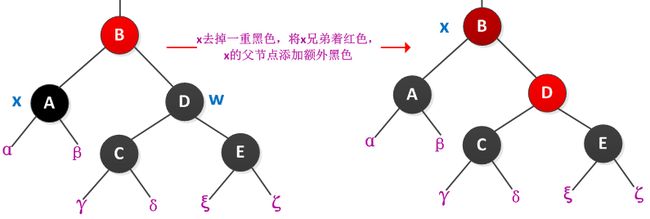
情况3:x的兄弟w是黑色的,w的左孩子是红色的,右孩子是黑色的
交换w和其左孩子left[w]的颜色,并对w进行右旋转。旋转后x的新兄弟w是一个有红色右孩子的黑结点,转换成了情况4。处理过程如下图所示: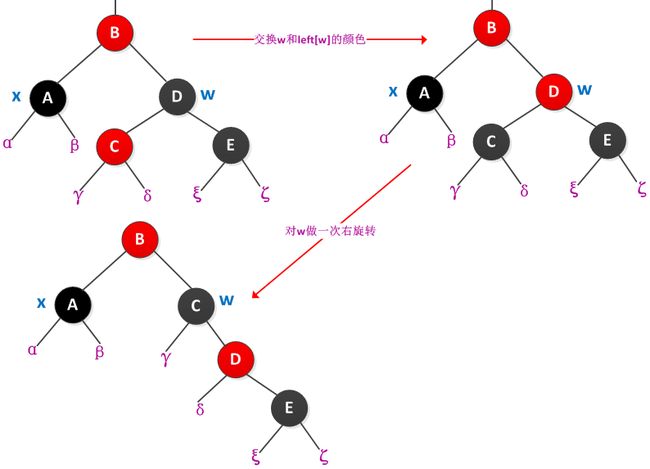
情况4:x的兄弟w是黑色的,而且w的右孩子是红色的。
执行过程是将w的颜色设置为parent[x]的颜色,将parent[x]的颜色设置为黑色,将w的右孩子着为黑色,然后在parent[x]做一次右旋,最后将x设置为根root。处理过程如下图所示:
【算法导论13章 P183】书中给出的伪代码:
// 伪代码
RB-TRANSPLANT( T, u, v ) // v替换u
if u.p == T.nil
T.root = v
else if u = u.p.left
u.p.left = v
else
u.p.right = v
v.p = u.p
RB-DELETE( T, z )
y = z
y-original-color = y.color
if z.left == T.nil
x = z.right
RB-TRANSPLANT( T, z, z.right )
else if z.right == T.nil
x = z.left
RB-TRANSPLANT( T, z, z.left )
else
y = TREE-MINIMUM( z.right )
y-original-color = y.color
x = y.right
if y.p == z
x.p = y
else
RB-TRANSPLANT( T, y, y.right )
y.right = z.right
y.right.p = y
RB-TRANSPLANT( T, z, y )
y.left = z.left
y.left.p = y
y.color = z.color
if y-original-color == BLACK
RB-DELETE-FIXUP( T, x )
RB-DELETE-FIXUP( T, x )
while x != T.root and x.color == BLACK
if x == x.p.left
w = x.p.right
if w.color == RED
w.color = BLACK
x.p.color = RED
LEFT-ROTATE( T, x.p )
w = x.p.right
if w.left.color == BLACK and w.right.color == BLACK
w.color = RED
x = x.p
else if w.right.color == BLACK
w.color = RED
w.left.color = BLACK
RIGHT-ROTATE( T, w )
w = x.p.right
w.right.color = BLACK
w.color = x.p.color
x.p.color = BLACK
LEFT-ROTATE( T, x.p )
x = T.root
else
( sanme as then clause with "right" and "left" exchanged )
x.color = BLACK4.对于删除y节点,有几种考虑。
1. 若y为红色,则这种情况如上述”第一“所述,并不影响平衡性。(null视为黑色)
2. 若y为黑色,则删除y后,x替换了y的位置,这样x子树相对于兄弟节点w为根的子树少了一个黑节点,影响平衡,需要进行调整。
剩下的调整工作就是将x子树中找一合适红色节点,将其置黑,使得x子树与w子树达到平衡。
若x为红色,直接将x置为黑色,即可达到平衡;
![]()
若x为黑色,则分下列几种情况。
![]()
情况1:x的兄弟w为红色。根据红黑性质,可得出w的儿子必然全黑,w父亲p也为黑。
![]()
改变p与w的颜色,同时对p做一次左旋,这样就将情况1转变为情况2,3,4的一种。
情况2:x的兄弟w为黑色,w的两个子结点都是黑色。可得出x与w的父亲颜色可红可黑。
![]()
因为x子树相对于其兄弟w子树少一个黑色节点,可以将w置为红色,这样,x子树与w子树黑色节点一致,保持了平衡。
new x为x与w的父亲。new x相对于它的兄弟节点new w少一个黑色节点。如果new x为红色,则将new x置为黑,则整棵树平衡。否则,
情况2转换为情况1,3,4
【注】情况2与情况3/4只能执行一个分支,情况3是情况4的预处理。
情况3:w为黑色,w左孩子红色,右孩子黑色。
![]()
交换w与左孩子的颜色,对w进行右旋。转换为情况4
情况4:w为黑色,右孩子为红色。
![]()
交换w与父亲p颜色,同时对p做左旋。这样左边缺失的黑色就补回来了,同时,将w的右儿子置黑,这样左右都达到平衡。
个人认为这四种状况比较难以理解,总结了一下。情况2是最好理解的,减少右子树的一个黑色节点,使x与w平衡,将不平衡点上移至x与w的父亲。
进行下一轮迭代。情况1:如果w为红色,通过旋转,转成成情况1,2,3进行处理。而情况3转换为情况4进行处理。也就是说,情况4是最接近最终解
的情况。情况4:右儿子是红色节点,那么将缺失的黑色交给右儿子,通过旋转,达到平衡。