力扣算法学习

1 两数之和

• 题目：给定一个整数数组 nums 和一个目标值 target，找出和为目标值的那 两个 整数，并返回他们的数组下标。

• 分析：暴力法、一遍哈希

• 核心代码：

• complement = target - nums[i];

• map.containsKey(complement

public class TwoNum {
    // 暴力法
    public int[] twoSum(int[] nums, int target) {
        for (int i = 0; i < nums.length; i++) {
            for (int j = i + 1; j < nums.length; j++) {
                if ((nums[i] + nums[j]) == target) {
                    return new int[]{i, j};
                }
            }
        }
        throw new IllegalArgumentException("No two sum solution");
    }

    // 一遍hashMap
    public int[] twoSum1(int[] nums, int target) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            int complement = target - nums[i];
            if (map.containsKey(complement)) {
                return new int[]{map.get(complement), i};
            }
            //map中存(数，下标)
            map.put(nums[i], i);
        }
        throw new IllegalArgumentException("No two sum solution");
    }
}

2 两数相加

题目：给出两个非空的链表表示两个非负的整数。 生成一个各自位数上和的新链表，按照逆序读出

核心代码：

• sum = x + y + carry;
• carry = sum / 10;
• current.next = new ListNode(sum % 10);

public class addTwoNumbers {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        // 相当于头结点，返回的是它的next结点
        ListNode resultNode = new ListNode(0);
        ListNode p = l1, q = l2, current = resultNode;
        // 进位值carry
        int carry = 0;
        // p、q遍历到末尾
        while (p != null || q != null) {
            int x = (p != null) ? p.val : 0;
            int y = (q != null) ? q.val : 0;
            // 每一位都开始求和，carry每次都加上
            int sum = x + y + carry;
            // sum/10取高位值
            carry = sum / 10;
            // sum%10取末尾
            current.next = new ListNode(sum % 10);
            current = current.next;
            if (p != null) {
                p = p.next;
            }
            if (q != null) {
                q = q.next;
            }
        }
        // 如果到最后还进位，就再生成一个进位值的新结点
        if (carry > 0) {
            current.next = new ListNode(carry);
        }
        // 返回结果值头结点的下一个结点开始的链表
        return resultNode.next;
    }
}

class ListNode {
    int val;
    ListNode next;

    ListNode(int x) {
        val = x;
    }
}

3 最长无重复子串长度

• 题目：给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度

• 例子：

  输入: "abcabcbb"
  输出: 3 
  解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。
  

• 滑动窗口法：左指针不变，右指针枚举不重复元素存入HashSet中；左指针发生改变，移除HashSet中重复上一个元素

• 核心代码：right + 1 < n && !set.contains(s.charAt(right + 1))

/**
 * 求出一个字符串中的无重复子串的长度
 */
public class LengthOfLongestSubstring {
    public int lengthOfLongestSubstring(String s) {
        // 哈希Set不能存放重复元素
        HashSet<Character> set = new HashSet<>();
        int n = s.length();
        // 右指针：right 最长无重复长度：ans
        int right = -1, ans = 0;
        // 左指针：i
        for (int i = 0; i < n; i++) {
            if (i != 0) {
                // 左指针向右移一个单位，set中移除所有左指针指向的元素
                set.remove(s.charAt(i - 1));
            }
            // 左指针i=0的时候，右指针不断枚举不含重复元素的值加入set
            while (right + 1 < n && !set.contains(s.charAt(right + 1))) {
                set.add(s.charAt(right + 1));
                right++;
            }
            // 每次长度差都发生变化，取和上次长度差的较大值赋给ans
            ans = Math.max(ans, right - i + 1);
        }
        return ans;
    }
}

4 两个数组的中位数

• 题目：要求在两个数组中找出中位数，时间复杂度O(log(m+n))。此题得多看
• 例子：力扣4题解：两个正序数组中位数

nums1 = [1, 3]
nums2 = [2]

则中位数是 2.0

• 分析：出现log就是二分查找，k表示查找出第k小的元素
• 用一个例子说明上述算法。假设两个有序数组如下：

A: 1 3 4 9
B: 1 2 3 4 5 6 7 8 9

• 两个有序数组的长度分别是 4和 9，长度之和是 12，中位数是两个有序数组中的第 7 个元素，因此需要找到第 k=7个元素

• 比较两个有序数组中下标为 k/2-1=2 的数，即如下面所示：

A: 1 3 4 9
       ↑
B: 1 2 3 4 5 6 7 8 9
       ↑

• 较小的数前面值（包括本身）丢弃，B：[1，2，3]被淘汰，同时更新 k 的值：k=k-k/2=7-3=4。

• 下一步寻找，比较两个有序数组中下标为 k/2-1=1k/2−1=1 的,如下面所示，其中方括号部分表示已经被排除的数。

A: 1 3 4 9
     ↑
B: [1 2 3] 4 5 6 7 8 9
             ↑

• 同理，A：[1,3]较小数被丢弃，同时更新 k 的值：k=k-k/2=2k=k−k/2=2。

• 下一步寻找，如下面所示，其中方括号部分表示已经被排除的数。

A: [1 3] 4 9
         ↑
B: [1 2 3] 4 5 6 7 8 9
           ↑

• 两数等于时候，放弃A[4]，同时更新 kk 的值： k=k-k/2=1k=k−k/2=1。
• 二分递归结束条件：k=1.返回两数中较小的数就是中位数=4

A: [1 3 4] 9
           ↑
B: [1 2 3] 4 5 6 7 8 9
           ↑

public class FindMedianSortedArrays {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int length1 = nums1.length;
        int length2 = nums2.length;
        int totalLength = length1 + length2;
        // 正序数组判断奇数==1就行，标准写法是！=0
        // 总数是奇数
        if (totalLength % 2 == 1) {
            int midIndex = totalLength / 2;
            // 第k个元素=下标+1,因为第1个数=num[0]
            double median = getKElement(nums1, nums2, midIndex + 1);
            return median;
        } else {
            int midIndex1 = totalLength / 2 - 1;
            int midIndex2 = totalLength / 2;
            int totalNum = getKElement(nums1, nums2, midIndex1 + 1) + getKElement(nums1, nums2, midIndex2 + 1);
            double median = totalNum / 2.0;
            return median;
        }
    }

    // 找出两个正序数组中第K个元素
    private int getKElement(int[] nums1, int[] nums2, int k) {
        int length1 = nums1.length;
        int length2 = nums2.length;
        // 起始下标
        int index1 = 0;
        int index2 = 0;
        // 二分查找变型
        while (true) {
            // 边界情况
            // 如果一个数组长度到头或者为0，返回另一个数组第k元素下标=k-1
            if (index1 == length1) {
                return nums2[index2 + k - 1];
            } else if (index2 == length2) {
                return nums1[index1 + k - 1];
            }
            // 第一个元素，返回较小值
            if (k == 1) {
                return Math.min(nums1[index1], nums2[index2]);
            }
            // 正常情况
            // 二分查找，从第k/2的开始查找
            int half = k / 2;
            int newIndex1 = Math.min(index1 + half, length1) - 1;
            int newIndex2 = Math.min(index2 + half, length2) - 1;
            int pivot1 = nums1[newIndex1];
            int pivot2 = nums2[newIndex2];
            // 较小数前面部分丢弃（包含本身）,newIndex前移
            // 注意：这里的第k个数 =下标+1
            if (pivot1 <= pivot2) {
                k -= (newIndex1 - index1 + 1);
                index1 = newIndex1 + 1;
            } else {
                k -= (newIndex2 - index2 + 1);
                index2 = newIndex2 + 1;
            }
        }
    }
}

5 最长回文字符串

• 题目：找出一个字符串的最长回文子串（回文串：正反读都一样）
• 暴力法：速度最慢
  1. 子串长度<2，本身就是最大回文串
  2. 将字符串转换成字符数组，防止下标越界
  3. 两次遍历判断出最长回文长度，返回子串

// 暴力法
    public String longestPalindrome1(String s) {
        int n = s.length();
        if (n < 2) {
            return s;
        }
        char[] sCharArray = s.toCharArray();
        int strLen = 1;
        int index = 0;
        for (int i = 0; i < n - 1; i++) {
            for (int j = i + 1; j < n; j++) {
                // 枚举所有长度>2的子串
                if (j - i + 1 > strLen && isPalindrome(sCharArray, i, j)) {
                    strLen = j - i + 1;
                    index =i;
                }
            }
        }
        return s.substring(index,index+strLen);
    }

    private boolean isPalindrome(char[] charArray, int i, int j) {
        while (i < j) {
            if (charArray[i] != charArray[j]) {
                return false;
            }
            i++;
            j--;
        }
        return true;
    }

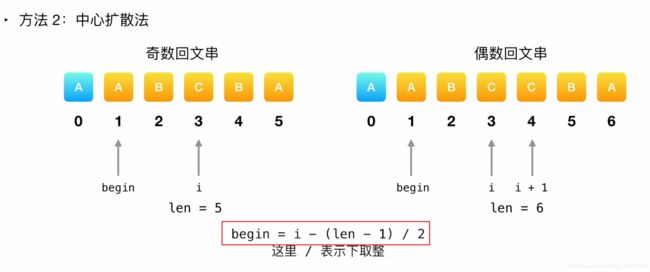
• 中心扩散法：速度是前三种最快的
  1. 遍历前步骤和暴力法相同
  2. 编写expandAroundCenter方法计算出字符串中心回文子串长度，分为奇偶两种情况，选最长那个
  3. 当前最>默认最长1，就交换最长，更改起始坐标；否则返回默认最长
     

// 中心扩散法
    public String longestPalindrome2(String s) {
        int n = s.length();
        if (n < 2) {
            return s;
        }
        char[] sCharArray = s.toCharArray();
        int maxLen = 1;
        int begin = 0;
        for (int i = 0; i < n - 1; i++) {
            // 奇数
            int oddLen = expandAroundCenter(sCharArray, i, i);
            // 偶数
            int evenLen = expandAroundCenter(sCharArray, i, i + 1);
            // 选长度大的
            int curMaxLen = Math.max(oddLen, evenLen);
            if (curMaxLen > maxLen) {
                maxLen = curMaxLen;
                // 画图发现规律
                begin = i - (maxLen - 1) / 2;
            }
        }
        return s.substring(begin, begin + maxLen);


    }

    private int expandAroundCenter(char[] charArray, int left, int right) {
        int len = charArray.length;
        int i = left;
        int j = right;
        // 从每个子串的中心开始判断
        while (i >= 0 && j < len) {
            if (charArray[i] == charArray[j]) {
                i--;
                j++;
            } else {
                break;
            }
        }
        // 跳出循环时，恰好s.charAt(i)!=s.charAt(j)
        // 回文长度是 j - i +1 -2 = j-i -1 长度不包含本身所以-2
        return j - i - 1;
    }

• 动态规划法：利用去掉两头还是回文串性质
  
  

// 动态规划法
    public String longestPalindrome3(String s) {
        int n = s.length();
        if (n < 2) {
            return s;
        }
        char[] sCharArray = s.toCharArray();
        int maxLen = 1;
        int begin = 0;
        // 初始化dp二维数组
        boolean[][] dp = new boolean[n][n];
        for (int i = 0; i < n; i++) {
            dp[i][i] = true;
        }
        // 从右上角开始填=先行再列
        for (int j = 1; j < n; j++) {
            for (int i = 0; i < j; i++) {
                if (sCharArray[i] != sCharArray[j]) {
                    dp[i][j] = false;
                } else {
                    // 边界条件满足：j-i<3 说明中间只能有1个或0个元素，就保证肯定是回文串
                    if (j - i < 3) {
                        dp[i][j] = true;
                    } else {
                    // 中间元素>1个，就参考其他元素 = 状态转移
                        dp[i][j] = dp[i + 1][j - 1];
                    }
                }
                // 如果当前状态true，且当前长度差>上次最长长度
                if (dp[i][j] && j - i + 1 > maxLen) {
                    maxLen = j - i + 1;
                    begin = i;
                }
            }
        }
        return s.substring(begin, begin + maxLen);
    }

• ManaChar算法：速度最快，但是绝大多数面试、笔试都不会问，待学；

7 整数反转

• 题目：给出一个 32 位的有符号整数，你需要将这个整数中每位上的数字进行反转。

public class Reverse {
    public int reverse(int x) {
        int rev = 0;
        while (x != 0) {
            int pop = x % 10;
            x = x / 10;
            if (rev > (Integer.MAX_VALUE / 10) || ((rev == Integer.MAX_VALUE / 10) && pop > 7)) {
                return 0;
            } else if (rev < (Integer.MIN_VALUE / 10) || ((rev == Integer.MIN_VALUE / 10) && pop < (-8))) {
                return 0;
            }
            rev = rev * 10 + pop;
        }
        return rev;
    }

}

8 字符串转换成整数

使其能将字符串转换成整数。该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止
该字符串在有效的整数部分之后也可能会存在多余的字符，那么这些字符可以被忽略，它们对函数不应该造成影响。
注意：假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换，即无法进行有效转换。在任何情况下，若函数不能进行有效的转换时，请返回 0 。

 public int myAtoi(String str) {
        char[] chars = str.toCharArray();
        int n = chars.length;
        int idx = 0;
        // 去掉前导空格
        while (idx < n && chars[idx] == ' ') {
            idx++;
        }
        // 去掉空格以后到末尾
        if (idx == n) {
            return 0;
        }
        // 判断是否存在负号
        boolean negative = false;
        if (chars[idx] == '-') {
            //遇到负号
            negative = true;
            idx++;
        } else if (chars[idx] == '+') {
            // 遇到正号
            idx++;
        } else if (!Character.isDigit(chars[idx])) {
            // 其他符号
            return 0;
        }
        int ans = 0;
        while (idx < n && Character.isDigit(chars[idx])) {
            int digit = chars[idx] - '0';
            // 越界 返回最大或最小
            if (ans > (Integer.MAX_VALUE - digit) / 10) {
                // 本来应该是 ans * 10 + digit > Integer.MAX_VALUE，但是前面两者都有可能越界，所以移项表达
                return negative ? Integer.MIN_VALUE : Integer.MAX_VALUE;
            }
            // 正常计算
            ans = ans * 10 + digit;
            idx++;
        }
        return negative ? -ans : ans;
    }

10 正则表达式匹配

• 题目：给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

//'.' 匹配任意单个字符
//'*' 匹配零个或多个前面的那一个元素
 public boolean isMatch(String s, String p) {
        int m = s.length();
        int n = p.length();
        // dp表示s的前i个字符和前j个字符是否匹配
        boolean[][] dp = new boolean[m + 1][n + 1];
        // 两个空字符串匹配
        dp[0][0] = true;
        for (int i = 0; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (p.charAt(j - 1) == '*') {
                    dp[i][j] = dp[i][j - 2];
                    if (match(s, p, i, j - 1)) {
                        dp[i][j] = dp[i][j] || dp[i - 1][j];
                    }
                } else {
                    if (match(s, p, i, j)) {
                        dp[i][j] =dp[i-1][j-1];
                    }
                }
            }
        }
        return dp[m][n];
    }
    // 判端两字中间字符是否相同
    private boolean match(String s, String p, int i, int j) {
        // i=0,j=1是最初的开始，表示空字符串不与一个字符的字符串匹配
        if (i == 0) {
            return false;
        }
        // . 规定一定能匹配任意字符
        if (p.charAt(j - 1) == '.') {
            return true;
        }
        return s.charAt(i - 1) == p.charAt(j - 1);
    }

11 盛水最多的容器

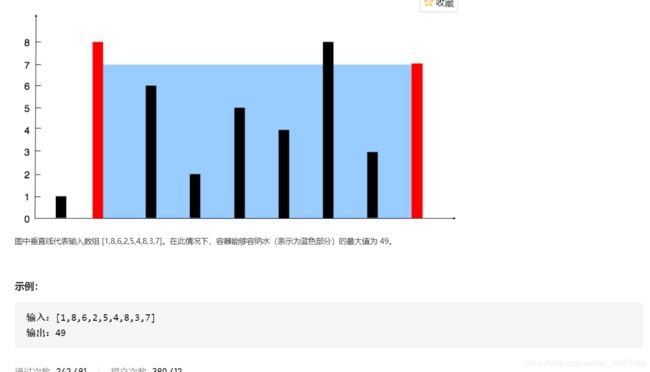
• 题目：给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

  说明：你不能倾斜容器，且 n 的值至少为 2。

// 双指针法
public int maxArea(int[] height) {
    int i = 0;
    int j = height.length - 1;
    int ans = 0;
    while (i < j) {
        int area = Math.min(height[i], height[j]) * (j - i);
        ans = Math.max(area, ans);
        // 每次都移动下的指针
        if (height[i] <= height[j]) {
            i++;
        } else {
            j--;
        }
    }
    return ans;
}

// 暴力破解
public int maxArea1(int[] height) {
    int ans = 0;
    int NowValue;
    for (int i = 0; i < height.length; i++) {
        for (int j = i; j < height.length; j++) {
            NowValue = Math.min(height[i], height[j]) * (j - i);
            ans = Math.max(NowValue,ans);
        }
    }
    return ans;
}

13 罗马数字转换

• 题目：罗马数字包含以下七种字符: I， V， X， L，C，D 和 M

• I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
  X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
  C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900

字符          数值
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

public int romanToInt(String s) {
        int sum = 0;
        // 获取第一位的值
        int preNum = getValue(s.charAt(0));
        for (int i = 1; i < s.length(); i++) {
            int nextNow = getValue(s.charAt(i));
            if (preNum < nextNow) {
                sum -= preNum;
            } else {
                sum += preNum;
            }
            preNum = nextNow;
        }
        // 此时preNum 就是最后一位的值，得加上
        sum += preNum;
        return sum;
    }

    private int getValue(char c) {
        switch (c) {
            case 'I':
                return 1;
            case 'V':
                return 5;
            case 'X':
                return 10;
            case 'L':
                return 50;
            case 'C':
                return 100;
            case 'D':
                return 500;
            case 'M':
                return 1000;
            default:
                return 0;
        }
    }

14 最长公共前缀

题目：编写一个函数来查找字符串数组中的最长公共前缀。如果不存在公共前缀，返回空字符串 ""。

 public String longestCommonPrefix(String[] strs) {
        if (strs.length == 0 || strs == null){
            return "";
        }
        String s1 = strs[0];
        for (int i = 1; i < strs.length; i++) {
            s1 = selectLongesCommonStr(s1, strs[i]);
            if (s1.length() == 0) {
                break;
            }
        }
        return s1;
    }

    private String selectLongesCommonStr(String s1, String s2) {
        int length = Math.min(s1.length(), s2.length());
        int index = 0;
        while (index < length && s1.charAt(index) == s2.charAt(index)) {
            index++;
        }
        // 跳出循环时，index = index+1，在substring中右边就正确
        return s1.substring(0, index);
    }

15 三数之和

题目：给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。

 public List<List<Integer>> threeSum(int[] nums) {
        int n = nums.length;
        List<List<Integer>> ans = new ArrayList<>();
        // 将nums从小到大排序
        Arrays.sort(nums);
        // 一指针从0开始枚举
        for (int i = 0; i < n; i++) {
            // 和上次枚举数不同
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            // 三指针指向数组最右端
            int k = n - 1;
            // 二指针从一指针后面开始枚举
            for (int j = i + 1; j < n; j++) {
                // 上次枚举数不同
                if (j > i + 1 && nums[j] == nums[j - 1]) {
                    continue;
                }
                // 二指针保证在三支针左边，并且三者加的数大于0，就三指针左移
                while (j < k && nums[i] + nums[j] + nums[k] > 0) {
                    k--;
                }
                // 如果二三指针重合，表示没有三数之和为0，跳出循环
                if (j == k) {
                    break;
                }
                if (nums[i] + nums[j] + nums[k] == 0) {
                    // 结果集是链表套链表
                    ArrayList<Integer> list = new ArrayList<>();
                    list.add(nums[i]);
                    list.add(nums[j]);
                    list.add(nums[k]);
                    ans.add(list);
                }
            }
        }
        return ans;
    }

17 电话号码的字母组合

• 题目：给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

public class LetterCom {
    List<String> ans = new ArrayList<>();

    Map<String, String> nums = new HashMap<String, String>() {{
        put("2", "abc");
        put("3", "def");
        put("4", "ghi");
        put("5", "jkl");
        put("6", "mno");
        put("7", "pqrs");
        put("8", "tuv");
        put("9", "wxyz");
    }};

    public List<String> letterCombinations(String digits) {
        if (digits.length() != 0) {
            callBack("", digits);
        }
        return ans;
    }

    /**
     * @param comb   组合结果
     * @param digits 数字
     */
    private void callBack(String comb, String digits) {
        // 递归结束提交时当前数字长度=0，往ans中加组合结果
        if (digits.length() == 0) {
            ans.add(comb);
        } else {
            // 获取数字串中的第一个数字
            String digit = digits.substring(0, 1);
            // 通过数字获得对应的全部字母
            String letters = nums.get(digit);
            // 全部字母递归
            for (int i = 0; i < letters.length(); i++) {
                String letter = nums.get(digit).substring(i, i + 1);
                // substring(1)从1开始到末尾
                callBack(comb + letter, digits.substring(1));
            }
        }
    }
}

19 删除倒数第n个节点的链表

• 题目：给定一个链表，删除链表的倒数第 n 个节点，并且返回链表的头结点。

public class RemoveNthFromEnd {
    // 两次遍历，第一次遍历找出长度;第二次遍历删除倒数第n个节点
    public ListNode removeNthFromEnd1(ListNode head, int n) {
        // 哑结点，在head的前一个结点
        ListNode ans = new ListNode(0);
        ans.next = head;
        int length = 0;
        // 遍历指针,先遍历head结点找出长度；再遍历哑结点
        ListNode i = head;
        // 注意别是i.next
        while (i != null) {
            length++;
            i = i.next;
        }
        length -= n;
        i = ans;
        // i遍历到length - 的位置
        while (length > 0) {
            length--;
            i = i.next;
        }
        // 删除倒数第n个节点
        i.next = i.next.next;
        // 返回ans.next，因为哑结点的下一个结点才是head
        return ans.next;

    }

    // 一次遍历法，i指针指向第n+1个节点;j从头开始遍历；i到达结尾时，i到j距离就是n
    public ListNode removeNthFromEnd2(ListNode head, int n) {
        ListNode ans = new ListNode(0);
        ans.next = head;
        // i、j的
        ListNode i = ans;
        ListNode j = ans;
        for (int k = 1; k <= n + 1; k++) {
            i = i.next;
        }
        while (i != null) {
            i = i.next;
            j = j.next;
        }
        j.next = j.next.next;
        return ans.next;
    }
}

20 有效的括号

题目：给定一个只包括 ‘(’，’)’，’{’，’}’，’[’，’]’ 的字符串，判断字符串是否有效。有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。

public class IsValid {
    // 存括号集合
    HashMap<Character, Character> mapperings;

    // 初始化括号存进map
    public IsValid() {
        mapperings = new HashMap<>();
        mapperings.put(')', '(');
        mapperings.put('}', '{');
        mapperings.put(']', '[');
    }

    public boolean isValid(String s) {
        // 初始化栈保存括号
        Stack<Character> stack = new Stack<>();

        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            if (mapperings.containsKey(c)) {
                // 匹配到闭括号，就出栈顶元素
                char topEle = stack.empty() ? '#' : stack.pop();
                // 如果栈顶元素不对因当前字符对应的开括号，就失败
                if (topEle != mapperings.get(c)) {
                    return false;
                }
            } else {
                // 没有匹配到闭括号，就进栈
                stack.push(c);
            }
        }
        // 返回栈是否为空的状态
        return stack.isEmpty();
    }
}

21 合并两个有序链表

• 题目：将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

class ListNode1 {
    int val;
    ListNode1 next;

    ListNode1() {
    }

    ListNode1(int val) {
        this.val = val;
    }

    ListNode1(int val, ListNode1 next) {
        this.val = val;
        this.next = next;
    }
}

public class MergeTwoLists {
    // 递归法
    public ListNode1 mergeTwoLists1(ListNode1 l1, ListNode1 l2) {
        if (l1 == null) {
            return l2;
        } else if (l2 == null) {
            return l1;
        }
        // 从较小值的那个链表开始递归
        else if (l1.val < l2.val) {
            l1.next = mergeTwoLists1(l1.next, l2);
            return l1;
        } else {
            l2.next = mergeTwoLists1(l1, l2.next);
            return l2;
        }
    }

    //迭代法
    public ListNode1 mergeTwoLists2(ListNode1 l1, ListNode1 l2) {
        ListNode1 preHead = new ListNode1(-1);
        ListNode1 pre = preHead;
        while (l1 != null && l2 != null) {
            // 每次选择值下的指向
            if (l1.val <= l2.val) {
                pre.next = l1;
                l1 = l1.next;
            } else {
                pre.next = l2;
                l2 = l2.next;
            }
            pre = pre.next;
        }
        //循环结束后，必有一个指向null，连接不null就行
        pre.next = (l1 == null) ? l2 : l1;
        return preHead.next;
    }
}

23 合成k个排序的链表

• 题目：合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。
• 待学递归和迭代法

public class MergeKLists {
    // 方法一：每次比较出minNode来合并链表
    public ListNode mergeKLists1(ListNode[] lists) {
        int n = lists.length;
        // 哑结点
        ListNode dummy = new ListNode(-1);
        ListNode tail = dummy;
        while (true) {
            // 创建最小值结点存最小值，最小值指针指向链表最小值下标
            ListNode minNode = null;
            int minPointer = -1;
            for (int i = 0; i < n; i++) {
                // 本次循环跳出
                if (lists[i] == null) {
                    continue;
                }
                // 遍历找出最小值结点和下标
                if (minNode == null || lists[i].val < minNode.val) {
                    minNode = lists[i];
                    minPointer = i;
                }
            }
            // 如果最小值下标是-1，结束循环
            if (minPointer == -1) {
                break;
            }
            // tail指针指向最小值结点
            tail.next = minNode;
            tail = tail.next;
            // 最小值结点指针后移重新比较
            lists[minPointer] = lists[minPointer].next;
        }
        return dummy.next;
    }

    // 方法一：使用pq小根堆优化方法二
    public ListNode mergeKLists2(ListNode[] lists) {
        // 使用优先级队列存小根堆,参数是选择结点值从小
        PriorityQueue<ListNode> pq = new PriorityQueue<>((v1, v2) -> v1.val - v2.val);
        // 将数组各个首结点，放入小根堆
        for (ListNode node : lists) {
            if (node != null) {
                pq.offer(node);
            }
        }
        // 创建哑结点
        ListNode dummy = new ListNode(-1);
        ListNode tail = dummy;
        // 遍历输出
        while (!pq.isEmpty()) {
            // 最小值结点指向根顶元素
            ListNode minNode = pq.poll();
            tail.next = minNode;
            tail = minNode;
            // 将首节点下一个结点放入根堆
            if (minNode.next != null) {
                pq.offer(minNode.next);
            }
        }
        return dummy.next;
    }

    // 后面待学迭代和递归
}

26 删除数组中重复的元素

• 题目：给定一个排序数组，你需要在 原地 删除重复出现的元素，使得每个元素只出现一次，返回移除后数组的新长度。不要使用额外的数组空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

public int removeDuplicates(int[] nums) {
        int i = 0;
        for (int j = 1; j < nums.length; j++) {
            if (nums[i] != nums[j]) {
                // 不等于先移动i指针，此时i指向的是相同的数
                // 如果先移动i，那么i指向的第一个数就丢失
                i++;
                // 相同的元素才能进行交换
                nums[i] = nums[j];
            }
        }
        // 数组长度=末尾数组下标+1
        return i + 1;
    }

28 实现strStr

• 题目：给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回 -1。

public class StrStr {
    // 滑动窗口法
    public int strStr1(String haystack, String needle) {
        if (needle.isEmpty() || needle.equals("")) {
            return 0;
        }
        int n = haystack.length();
        int l = needle.length();
        // 暴力，每一个长度的都比较，所以时间复杂度比较高
        for (int i = 0; i < n - l + 1; i++) {
            // 选择hay中的长度为l的子串与needle比较
            if (haystack.substring(i, i + l).equals(needle)) {
                return i;
            }
        }
        return -1;
    }

    // 双指针法
    public int strStr2(String haystack, String needle) {
        int n = haystack.length();
        int l = needle.length();
        if (l == 0) {
            return 0;
        }
        // 右指针遍历hay
        int pn = 0;
        // pn最末只能在hay中最后l长度的起始点
        while (pn < n - l + 1) {
            if (pn < n - l + 1 && haystack.charAt(pn) != needle.charAt(0)) {
                pn++;
            }
            int currentLen = 0;
            // 左指针遍历needle
            int pl = 0;
            while (pl < l && pn < n && haystack.charAt(pn) == needle.charAt(pl)) {
                pl++;
                pn++;
                currentLen++;
            }
            //如果needle匹配到
            if (currentLen == l) {
                return pn - l;
            }
            // 不匹配就回溯下标
            pn = pn - currentLen + 1;
        }
        // 如果循环没有返回，就返回失败
        return -1;
    }

}

29 两数相除

• 题目：给定两个整数，被除数 dividend 和除数 divisor。将两数相除，要求不使用乘法、除法和 mod 运算符。返回被除数 dividend 除以除数 divisor 得到的商。整数除法的结果应当截去（truncate）其小数部分，例如：truncate(8.345) = 8 以及 truncate(-2.7335) = -2
• 注意：
  • 被除数和除数均为 32 位有符号整数。除数不为 0。
  • 假设我们的环境只能存储 32 位有符号整数，其数值范围是 [−2^31, 2^31 − 1]。本题中，如果除法结果溢出，则返回 2^31−1

public class Divide {
    public int divide(int dividend, int divisor) {
        // 符号位:全正为false，有负为true
        boolean sign = (dividend > 0) ^ (divisor > 0);
        // 正数边界问题麻烦，转换成负数
        // 需要看jdk源码学习Integer
        if (dividend > 0) {
            dividend = -dividend;
        }
        if (divisor > 0) {
            divisor = -divisor;
        }
        int res = 0;
        // 负数 大的反而小：-10,-3
        while (dividend <= divisor) {
            int res1 = -1;
            int divisor1 = divisor;
            // 时间复杂度最快就是2分查找
            while (dividend <= (divisor1 << 1)) {
                // 边界条件
                if (divisor1 <= (Integer.MIN_VALUE >> 1)) {
                    break;
                }
                res1 = res1 << 1;
                divisor1 = divisor1 << 1;
            }
            // 11-6=5，再次二分
            dividend = dividend - divisor1;
            // 这里是+，结果再用！sign存在，就转成正数
            res += res1;
        }
        // !sign==true，表示正数
        if (!sign) {
            if (res <= Integer.MIN_VALUE) {
                return Integer.MAX_VALUE;
            }
            res = -res;
        }
        return res;
    }

    public static void main(String[] args) {
        // -2147483648
        System.out.println(Integer.MIN_VALUE);
        // java中负最小整数相反数还是本身：-2147483648
        // 所以负数时候存在越界问题
        System.out.println(-Integer.MIN_VALUE);
        // -2147483647
        System.out.println(-Integer.MAX_VALUE);
        // 无符号左移就是扩大2倍
        System.out.println(-4 << 1);
        // ^异或：相同为0 不同为1
        System.out.println((true) ^ (false));
    }
}

33 搜索旋转排序数组

• 题目：假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

  搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。算法时间复杂度必须是 O(log n) 级别

public class Search {
    // 法一：利用二分查找和nums[0],nums[mid]做比较，转换成有序数组找目标值
    public int search1(int[] nums, int target) {
        int low = 0;
        int hight = nums.length - 1;
        while (low <= hight) {
            int mid = low + (hight - low) / 2;
            // 二分循环结束条件
            if (target == nums[mid]) {
                return mid;

            }
            // 目标值在nums[0]右边,中间值比nums[0]还小，就换成最大值，使得数组变成有序
            if (target >= nums[0]) {
                if (nums[mid] < nums[0]) {
                    nums[mid] = Integer.MAX_VALUE;
                }
            } else {
                if (nums[mid] >= nums[0]) {
                    nums[mid] = Integer.MIN_VALUE;
                }
            }
            // 数组有序后，就使用二分查找
            if (target > nums[mid]) {
                low = mid + 1;
            } else {
                hight = mid - 1;
            }
        }
        return -1;
    }
    // 直接分类讨论
    public int search2(int[] nums, int target) {
        int low = 0;
        int hight = nums.length - 1;
        while (low <= hight) {
            int mid = low + (hight - low) / 2;
            // 二分循环结束条件
            if (target == nums[mid]) {
                return mid;

            }
            // 直接分类讨论，左右边界加等于
            if (nums[0] <= nums[mid]) {
                if (target >= nums[low] && target < nums[mid]) {
                    hight = mid - 1;
                } else {
                    low = mid + 1;
                }
            } else {
                if (target > nums[mid] && target <= nums[hight]) {
                    low = mid + 1;
                } else {
                    hight = mid - 1;
                }
            }
        }
        return -1;
    }

}

34 在排序数组中查找出第一个和最后一个目标元素下标

• 题目：给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

  你的算法时间复杂度必须是 O(log n) 级别。如果不存在，就返回{-1.-1}

public class SearchRange {
    public int[] searchRange(int[] nums, int target) {
        if (nums == null) {
            return new int[]{-1, -1};
        }
        int firstInx = find(true, nums, target);
        int lastInx = find(false, nums, target);
        return new int[]{firstInx, lastInx};
    }

    private int find(boolean isFindFirstIndex, int[] nums, int target) {
        int low = 0;
        int hight = nums.length - 1;
        while (low <= hight) {
            int mid = low + (hight - low) / 2;
            if (nums[mid] > target) {
                hight = mid - 1;
            } else if (nums[mid] < target) {
                low = mid + 1;
            } else if (nums[mid] == target) {
                // 标识位表示是否查找第一个或最后一个目标位
                // 第一个位置就查找中间位置的左边
                if (isFindFirstIndex) {
                    // 保证前后两个位置不相同就返回，相同就改变下标
                    if (mid > 0 && nums[mid] == nums[mid - 1]) {
                        hight = mid - 1;
                    } else {
                        return mid;
                    }
                } else {
                    if (mid < nums.length - 1 && nums[mid] == nums[mid + 1]) {
                        low = mid + 1;
                    } else {
                        return mid;
                    }
                }
            }
        }
        return -1;
    }
}

36 有效的数独

• 题目：判断一个 9x9 的数独是否有效。只需要根据以下规则，验证已经填入的数字是否有效即可。
  • 数字 1-9 在每一行只能出现一次。
  • 数字 1-9 在每一列只能出现一次。
  • 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

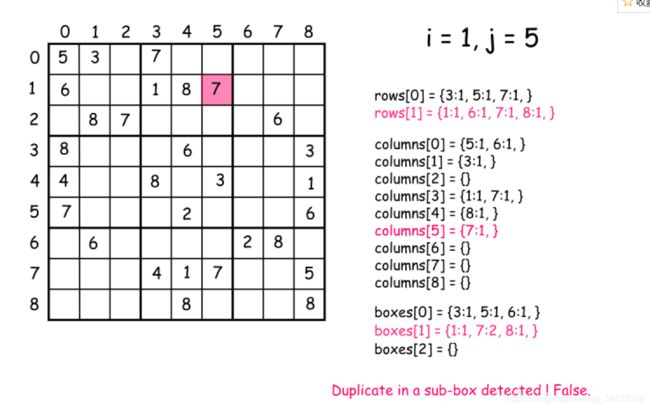
学习：使用map.getOrDefault()来判断是否存在过元素

public boolean isValidSudoku(char[][] board) {
        // 创建三个map分别存行、列、3*3序列
        HashMap<Integer, Integer> [] rows = new HashMap[9];
        HashMap<Integer, Integer> [] columns = new HashMap[9];
        HashMap<Integer, Integer> [] boxes = new HashMap[9];
        // 每个数组元素也是一个map
        for (int i = 0; i < 9; i++) {
            rows[i] = new HashMap<Integer, Integer>();
            columns[i] = new HashMap<Integer, Integer>();
            boxes[i] = new HashMap<Integer, Integer>();
        }
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                char cnum = board[i][j];
                if (cnum != '.') {
                    int n = (int) cnum;
                    // 3*3子数独的下标
                    int box_index = (i / 3) * 3 + j / 3;
                    // map.getOrDefault检查是否有key，有就输出，无就填入指定默认值
                    rows[i].put(n, rows[i].getOrDefault(n, 0) + 1);
                    columns[j].put(n, columns[j].getOrDefault(n, 0) + 1);
                    boxes[box_index].put(n, boxes[box_index].getOrDefault(n, 0) + 1);
                    if (rows[i].get(n) > 1 || columns[j].get(n) > 1 || boxes[box_index].get(n) > 1) {
                        return false;
                    }
                }
            }
        }
        return true;
    }