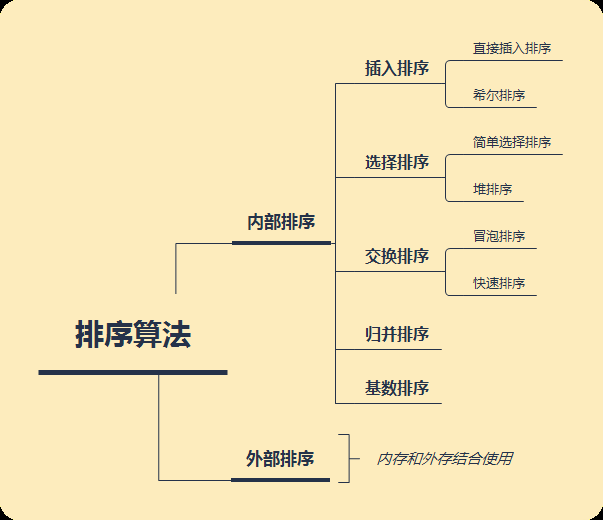
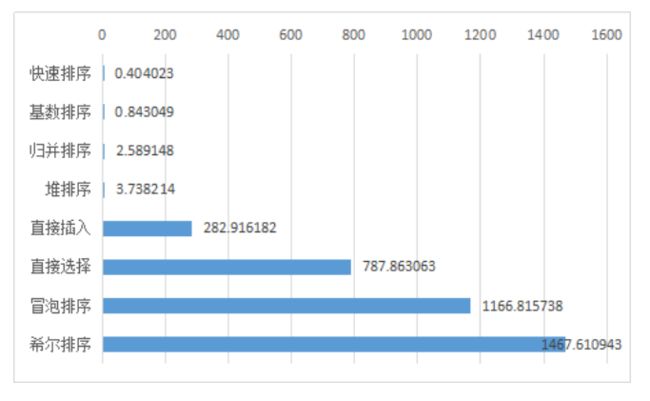
直接插入排序
时间复杂度:O(n²)
空间复杂度:O(1)
稳定性:稳定
算法思想:假设待排序的数据是数组A[1….n]。初始时,A[1]自成1个有序区,无序区为A[2….n]。在排序的过程中,依次将A[i] (i=2,3,….,n)从后往前插入到前面已排好序的子数组A[1,…,i-1]中的适当位置,当所有的A[i] 插入完毕,数组A中就包含了已排好序的输出序列。
def insert_sort(array): # 定义直接插入排序的函数,将需要排序的数组作为形参
for i in range(len(array)): # 从头依次循环,并取循环坐标作为下一循环的节点
for j in range(i): # 从头开始,循环到第一循环循环到的数为止
if array[i] > array[j]: # 判断第一循环坐标的值是否大于第二循环坐标的值
array.insert(j, array.pop(i)) # 判断结果为真则将值小的数置前
return array # 返回排好序之后的数组
希尔排序
时间复杂度:O(n)
空间复杂度:O(n√n)
稳定性:不稳定
算法思想:希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
def shell_sort(array):
gap = len(array) # 设置增量
while gap > 1:
gap = gap // 2 # 选择增量,当所有的数被分为一组的时候即退出循环
for i in range(gap, len(array)): # 分组
for j in range(i % gap, i, gap): # 设置增量为步进,实现比较每组数大小的效果
if array[i] < array[j]: # 判断后将数值小的数组元素置前
array[i], array[j] = array[j], array[i]
return array
简单选择排序
时间复杂度:O(n²)
空间复杂度:O(1)
稳定性:不稳定
算法思想:每一趟从待排序的数据元素中选择最小(或最大)的一个元素作为首元素,直到所有元素排完为止,简单选择排序是不稳定排序。
def select_sort(array):
for i in range(len(array)): # 每取一个值,可以看做是一趟
x = i # min index
for j in range(i, len(array)): # 遍历数组,与取出的元素进行比较
if array[j] < array[x]: # 取当前趟次最小元素,置于已经遍历过的数据之前
x = j
array[i], array[x] = array[x], array[i]
return array
堆排序
时间复杂度:O(nlog₂n)
空间复杂度:O(1)
稳定性:不稳定
算法思想:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
def heap_sort(array):
def heap_adjust(parent): # 构造初始堆并比较近似完全二叉树中节点的值
child = 2 * parent + 1 # 左孩子节点
while child < len(heap):
if child + 1 < len(heap):
if heap[child + 1] > heap[child]:
child += 1 # 右孩子节点
if heap[parent] >= heap[child]: # 父节点大于右孩子节点便结束循环
break
heap[parent], heap[child] = heap[child], heap[parent] # 交换左孩子节点与父节点的值,使大数后沉
parent, child = child, 2 * child + 1
heap, array = array.copy(), []
for i in range(len(heap) // 2, -1, -1):
heap_adjust(i)
while len(heap) != 0: # 使所有的数都经过比较
heap[0], heap[-1] = heap[-1], heap[0]
array.insert(0, heap.pop())
heap_adjust(0)
return array
https://blog.csdn.net/MoreWindows/article/details/6709644
http://www.cnblogs.com/dolphin0520/archive/2011/10/06/2199741.html
https://www.cnblogs.com/chengxiao/p/6129630.html
http://images.cnblogs.com/cnblogs_com/kkun/201111/201111301912294099.gif
冒泡排序
时间复杂度:O(n²)
空间复杂度:O(1)
稳定性:稳定
算法思想:对相邻的元素进行两两比较,顺序相反则进行交换,这样,每一趟会将最小或最大的元素“浮”到顶端,最终达到完全有序。
def bubble_sort(array):
for i in range(len(array)):
for j in range(i, len(array)):
if array[i] > array[j]: # 若前面的数大于后面的数,则交换位置
array[i], array[j] = array[j], array[i]
return array
快速排序
时间复杂度:O(nlog₂n)
空间复杂度:O(nlog₂n)
稳定性:不稳定
算法思想:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
def quick_sort(array):
def recursive(begin, end):
if begin > end:
return
l, r = begin, end
pivot = array[l] # 定义标准,也就是本次执行结束之后找到自己位置的那个数
while l < r: # 利用while循环从开始到结尾依次与标准比较
while l < r and array[r] > pivot: # 比标准大的数,放到右边
r -= 1
while l < r and array[l] <= pivot: # 比标准小的数,放到左边
l += 1
array[l], array[r] = array[r], array[l] # 若不满足上述条件,左右调换
array[l], array[begin] = pivot, array[l] # 标准找到自己位置
recursive(begin, l - 1) # 左边调用,即:对比已经找到位置的数小的数进行排序
recursive(r + 1, end) # 右边调用,即:对比已经找到位置的数大的数进行排序
recursive(0, len(array) - 1) # 调用一次方法,一个数找到正确位置,下次参与排序的数-1
return array
http://www.cnblogs.com/foreverking/articles/2234225.html
归并排序
时间复杂度:O(nlog₂n)
空间复杂度:O(1)
稳定性:稳定
算法思想:是创建在归并操作上的一种有效的排序算法,效率为O(n log n)。1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用,且各层分治递归可以同时进行。(先分后治再合并)
def merge_sort(array):
def merge_arr(arr_l, arr_r): # 先治后合
array = []
while len(arr_l) and len(arr_r): # 治
if arr_l[0] <= arr_r[0]: # 右边的组数大,就添加左边的数到下一组
array.append(arr_l.pop(0)) # 判断一个,取出一个,直到全部取完
elif arr_l[0] > arr_r[0]: # 左边的组数大,就添加右边的数到下一组
array.append(arr_r.pop(0))
if len(arr_l) != 0: # 合
array += arr_l # 合左边
elif len(arr_r) != 0:
array += arr_r # 合右边
return array
def recursive(array): # 分
if len(array) == 1: # 分到最小单位
return array
mid = len(array) // 2 # 对二取整,切片划分数组
arr_l = recursive(array[:mid])
arr_r = recursive(array[mid:])
return merge_arr(arr_l, arr_r) # 一分为二
return recursive(array)
https://www.cnblogs.com/chengxiao/p/6194356.html
基数排序
时间复杂度:O(d(r+n))
空间复杂度:O(rd+n)
稳定性:稳定
算法思想:将整数按位数切割成不同的数字,然后按每个位数分别比较。
def radix_sort(array):
bucket, digit = [[]], 0 # 初始化桶数组和数位控制
while len(bucket[0]) != len(array): # 判断是否将所有位数取出
bucket = [[], [], [], [], [], [], [], [], [], []] # 设置桶数组
for i in range(len(array)):
num = (array[i] // 10 ** digit) % 10 # 取当前位数
bucket[num].append(array[i]) # 放入相应的桶中
array.clear() # 清楚当前数据
for i in range(len(bucket)):
array += bucket[i] # 将排好序的桶数组添加进数组
digit += 1 # 数位控制
return array
https://www.cnblogs.com/skywang12345/p/3603669.html